Le regole del gioco possono prevedere modalità di svolgimento differenti. Particolare rilevanza assumono le regole riguardanti la sequenza temporale delle decisioni che verranno prese dai singoli giocatori.

In particolare occorre distinguere tra:

• giochi simultanei (statici): in cui i giocatori prendono le decisioni contemporaneamente (ad esempio: morra cinese, tocco, gara d'asta per un appalto);
• giochi sequenziali (dinamici): in cui giocatori non scelgono simultaneamente, ma seguono un ordine prestabilito dalle "regole del gioco" (ad esempio: scacchi,dama).

Inoltre le "regole del gioco" possono prevedere che il gioco stesso possa essere ripetuto un certo numero di volte, una volta sola o un numero infinito o non conosciuto di volte.

Infine i giochi possono avere carattere competitivo o cooperativo (giochi di coordinamento).

Secondo la natura delle interazioni fra i partecipanti, la classificazione di base è tra giochi non cooperativi (di cui la teoria dei giochi si occupa in misura 323h75d prevalente) e giochi cooperativi. I primi sintetizzano dinamiche per cui ciascun soggetto persegue il proprio interesse senza considerare guadagni/perdite altrui. Nei secondi, i soggetti si coalizzano assumendo reciproci impegni; la questione centrale non è più cercare di anticipare la mossa dell'altro, bensì come ripartirsi il surplus derivante dalla cooperazione.

Fra i primi un'ulteriore classificazione si fonda sull'ammontare e sulla distribuzione tra gli avversari dei pay-offs:

• giochi a somma variabile (come il dilemma del prigioniero);
• giochi a somma costante (scacchi, briscola, poker.).

Infine una caratteristica molto importante dei giochi cooperativi è la possibilità di sottoscrivere accordi vincolanti, in caso contrario I giochi saranno non cooperativi.

Un gioco si dice a somma zero quando la somma dei pay-off di ogni cella della matrice (indipendentemente dal mix di strategie selezionate) equivale a zero.

Più in generale un gioco è a somma costante quando la somma dei pay-off di ogni cella è costante, mentre ne muta l'allocazione fra giocatori in funzione dell'esito del gioco.

Questi giochi oltre ad essere non cooperativi, sono anche molto conflittuali (giochi di "puro conflitto") poiché ciò che guadagna uno è esattamente pari a ciò che perde l'altro.

esempi di giochi a somma zero.

esempio di gioco a somma costante.

Diremo invece che un gioco è a somma variabile quando l'ammontare complessivo del pay-off varia in corrispondenza di ciascun esito del gioco.

Al contrario dei giochi a somma costante, nei giochi a somma variabile può sussistere qualche convergenza di interessi tra i giocatori.

Tale convergenza diviene perfetta nel caso dei giochi di "pura collaborazione" caratterizzati dal fatto che, in ogni cella, i pay-off dei due giocatori sono identici.

esempi di giochi di pura collaborazione.

Tra gli estremi del puro conflitto e della pura collaborazione, vi sono tutti i casi intermedi rappresentati dai "giochi con movente misto" (Schelling), cioè da quei giochi a somma variabile nei quali la struttura dei pay-off esibisce una qualche combinazione di conflitto e collaborazione.

esempi di giochi con movente misto.

Sotto il profilo informativo è possibile distinguere tra: giochi ad informazione perfetta, imperfetta e ad informazione completa e incompleta.

Nei giochi a informazione perfetta ogni giocatore conosce tutte le mosse eseguite dagli altri giocatori (gli scacchi e la dama ne costituiscono classici esempi). I giochi a informazione perfetta sono necessariamente sequenziali, ovvero dinamici, in questo modo la mossa del giocatore può essere effettivamente basata su una conoscenza completa del contesto.

Nei giochi a informazione completa si richiede invece che ogni giocatore abbia tutte le informazioni sul contesto e sulle strategie degli avversari, ma non necessariamente sulle loro azioni; per esempio, ai giocatori potrebbe essere chiesto di decidere contemporaneamente la propria mossa, in segreto, e poi giocarla contemporaneamente, quindi senza poter valutare preventivamente gli effetti nella mossa avversaria nell'elaborazione della propria strategia (un esempio in questo senso è il "dilemma del prigioniero").

Evidentemente, un gioco a informazione perfetta è anche un gioco a informazione completa, ma non è vero il contrario.

Il contesto informativo può essere parzialmente dedotto anche dalla rappresentazione del gioco. La forma estesa mette in risalto sia le informazioni di cui i giocatori dispongono al momento di muovere, sia la sequenza (temporale o logica) delle loro mosse.

Esistono due tipi fondamentali di modelli impiegati per rappresentare i giochi: forma strategica o normale e forma estesa.

Nel primo il gioco è rappresentato per mezzo di una matrice ed è composto da tre elementi:

una lista di partecipanti o giocatori;

una lista di strategie per ogni giocatore;

per ogni profilo di strategie la corrispondente lista di pagamenti (pay-off) che i giocatori ricevono.

rappresentazione di un gioco in forma strategica.

Il primo numero di ciascuna cella è il pay-off del giocatore 1, mentre il secondo numero è il pay-off del giocatore 2.

Le strategie a disposizione sono:

giocatore 1: ;

giocatore 2: ;

I possibili esiti del gioco sono quattro:

(A ; A), (A ; B), (B ; B), (B ; A)

Questo approccio può essere maggiormente utile per individuare strategie strettamente dominate ed equilibri di Nash, ma rispetto alla forma estesa alcune informazioni vengono trascurate.

In alternativa alla forma strategica troviamo la rappresentazione in forma estesa (introdotta da von Neumann e Morgenstern nel 1944 e formalizzata da Kuhn nel 1953) in cui il gioco è descritto mediante un "albero delle decisioni".

Un gioco in forma estesa è caratterizzato da sette elementi:

un insieme di giocatori tra i quali può rientrare la Natura;

un albero di gioco i cui nodi denotano situazioni strategiche;

un'attribuzione dei nodi ai giocatori che specifica a chi si riferisce ciascun nodo;

una lista di insiemi di informazione che indica quali nodi un giocatore può scegliere in ogni suo insieme di informazione;

un elenco di mosse o azioni che ciascun giocatore può scegliere in ogni suo insieme di informazione;

una funzione di vincita per ogni giocatore (esclusa al più la Natura);

un'eventuale distribuzione iniziale di probabilità sulle azioni della Natura.

Ogni nodo (chiamato nodo decisionale) rappresenta il complesso delle scelte effettuate in precedenza. S'inizia a giocare da un unico nodo iniziale e il gioco scorre attraverso l'albero lungo un percorso determinato dalle scelte effettuate dai giocatori fino a quando viene raggiunto un nodo terminale. Ai nodi terminali sono associati i pay-off assegnati ai giocatori. Ad ogni nodo non terminale è associato un giocatore: questo sceglie fra le mosse possibili in quel nodo, le quali sono rappresentate da un lato che conduce ad un altro nodo.

A differenza della forma strategica, la forma estesa consente la modellazione esplicita d'interazioni in cui un giocatore fa più di una mossa durante il gioco e la sua mossa può dipendere da diversi stati.

Ad ogni gioco in forma estensiva corrisponde un gioco in forma strategica in cui i giocatori scelgono in modo simultaneo fra le strategie che vogliono attuare, ma ad un particolare gioco in forma strategica possono corrispondere, in generale, diversi giochi in forma estensiva.

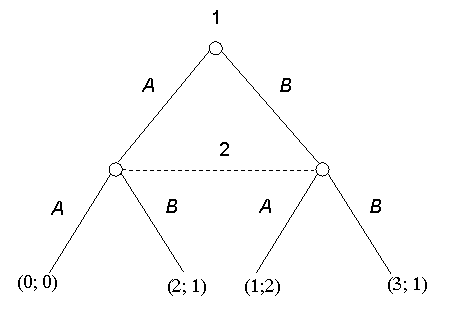
rappresentazione di un gioco in forma estesa.

I numeri che seguono il nodo terminale indicano il livello dei profitti dei due giocatori, il primo dei due numeri indica il profitto del giocatore 1 e il secondo si riferisce al profitto del giocatore 2.

La presenza di un legame tra più nodi rappresentato con una linea tratteggiata evidenzia il fatto che il giocatore in questione (giocatore 2) non sa con esattezza in quale nodo si trova. Se il set informativo comprendesse un solo nodo il gioco sarebbe ad informazione perfetta.

Viene indicato come supergioco l'intera struttura ad albero e viene definito come sottogioco (proprio) ciascun sottoinsieme del supergioco avente origine in un nodo singolo e contenente tutti i nodi successivi a quello di origine.

In un gioco in forma estesa ad ogni profilo di strategie non corrisponde un esito, ma una distribuzione di probabilità sugli esiti e sui vettori di vincita; questi vettori sono espressi in unità di utilità.