Macchine in corrente continua - Dinamo

Avvolgimento embricato & avvolgimento ondulato

Funzionamento a vuoto della dinamo

Reazione d'indotto della dinamo

Coppia elettromagnetica frenante nella dinamo

La commutazione nella dinamo

Avvolgimenti compensatori e poli ausiliari nella dinamo

Dinamo con eccitazione indipendente

Dinamo ad eccitazione derivata

Dinamo ad eccitazione serie

Dinamo ad eccitazione composta

Perdite e rendimento nella dinamo

Motori a corrente continua

Generalità e principio di funzionamento

Avviamento dei motori a corrente continua

Regolazione della velocità dei motori a corrente continua

Gruppi Ward-Leonard

Fuga del motore a corrente continua

Generalità sulle macchine in corrente continua

La macchina a corrente continua è una macchina elettrica rotante che trasforma energia elettrica in energia meccanica e viceversa. Essa, infatti, è una macchina reversibile, cioè può funzionare sia come generatore (chiamato comunemente dinamo) che trasforma energia meccanica in energia elettrica, e sia come motore che effettua la trasformazione inversa. La macchina a corrente continua, come le altre macchine rotanti, è costituita da due parti fondamentali di forma cilindrica coassiali:

- una parte esterna fissa (detta statore), sostenuta da un'incastellatura, che funziona da sistema induttore;    - una parte interna rotante (detta rotore), montata su un albero sostenuto da supporti, che funziona da sistema indotto. Tra le due parti c'è uno strato d'aria (0,5÷1mm²) detto traferro. Nella macchina a corrente continua, oltre alle parti fondamentali comuni a tutte le macchine rotanti, c'è un organo speciale detto collettore a lamelle montato sull'albero in modo coassiale. Le lamelle contigue del collettore, pur vicinissime, sono tra loro isolate. In coincidenza con gli interassi polari sono poi sistemate rigidamente le spazzole, ciascuna spazzola ha una larghezza sufficiente a farle toccare due lamelle contigue.

Il sistema induttore è ricavato nello statore della macchina: si compone di un nucleo di ferro massiccio che ha la funzione di convogliare il campo magnetico verso i poli (la cui espansione, detta anche scarpa polare, è realizzata mediante dei lamierini di Fe-Si per ridurre le perdite nel ferro dovute al pennellamento delle linee di campo magnetico nel passaggio dallo statore al rotore) e di un avvolgimento induttore eccitato in corrente continua Ie che ha lo scopo di generare il campo magnetico induttore.   

La parte del circuito magnetico che collega i poli della macchina è detto giogo; esso è attraversato dalla metà del flusso uscente da un polo ed è fatto generalmente di ghisa o di acciaio fuso.

Il sistema indotto è ricavato nel rotore ed è costituito: - da un nucleo realizzato con lamierini di Fe-Si in quanto il campo magnetico nel rotore è variabile; - e dall'avvolgimento d'indotto (chiamato anche armatura) chiuso in cortocircuito.

Principio di funzionamento della dinamo

Immaginiamo ora che l'avvolgimento induttore sia percorso dalla corrente d'eccitazione continua Ie [A] così che ciascun polo sia attraversato dal flusso costante Φ [Wb], inoltre il rotore sia trascinato alla velocità Ω [rad/s] da un motore primo esterno. I conduttori attivi dell'avvolgimento rotorico, tagliando le linee del campo magnetico induttore, saranno sede di f.e.m. indotte.

La f.e.m.i. in ogni conduttore, in cave contigue, può essere rappresentata con vettori e, uno di seguito all'altro (consecutivi), sfasati tra loro dell'angolo α esistente fra le cave. Essendo:

e = B l v senα e α = p · 360º / N

dove:

B è l'induzione magnetica[T];

l è la lunghezza del conduttore [m];

v è la velocità di taglio [m/s];

p è il numero di coppie polari;

N è il numero di conduttori attivi.

   

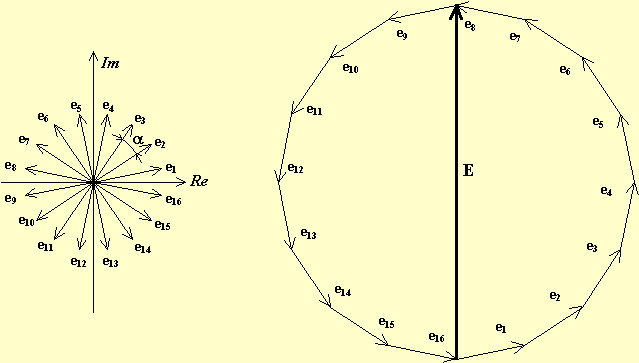
Nell'esempio di figura, essendo il numero di conduttori attivi N = 16 ed il numero di coppie polari p = 1, avremo . Gli N conduttori si trovano in serie tra loro così che è nulla la f.e.m. complessiva che agisce nell'indotto essendo 626i81g questa data dalla somma vettoriale di N vettori uguali in intensità e disposti a stella simmetrica. Non è invece nulla la somma delle f.e.m. di una metà dei conduttori, ad esempio la somma delle f.e.m. dei conduttori da 1 a 8 sarà pari ad E.

E' possibile determinare un'espressione approssimata della E. Infatti, se il numero di conduttori N è abbastanza grande (come accade in realtà), il poligono ottenuto sommando le f.e.m. negli N conduttori si può confondere con la circonferenza ad esso circoscritta.

Durante la rotazione, uno stesso conduttore si troverà alternativamente sotto i poli induttori Nord e Sud, così che la f.e.m. in ciascun conduttore sarà alternata nel tempo; più precisamente la f.e.m. istantanea in un conduttore è nulla quando il conduttore attraversa l'asse interpolare y - y o piano di inversione poiché il flusso si inverte.

La f.e.m. media è:

│ΔΦ│ Φ·p 2·Φ·p 60 2·p· ·n

em = --- = -- = --- [V] n = -- [g/1'] => em = ---- [V]

│Δ t│ T/2 T T 60

T

ove: Δ t è il tempo che il conduttore impiega per tagliare il flusso ed è pari a Δ t = -- ;

2·p

2∙p è il numero dei poli; n è la velocità di rotazione [giri/1'] e Ф è il flusso che esce da un polo [Wb]; T [s] è il tempo impiegato dal rotore a compiere un giro.

In definitiva, la somma vettoriale fra due punti diametricamente opposti della poligonale è la risultante E della f.e.m. che può essere prelevata dalle spazzole del collettore con lo stesso valore e con lo stesso verso (continua). La f.e.m. sviluppata (E) da una dinamo è uguale alla f.e.m. indotta di un ramo d'indotto o via interna (a). Essa si ottiene moltiplicando la f.e.m. media (em) di un conduttore attivo per il numero di conduttori attivi nel ramo (N).

N 2∙p∙n∙Ф 2∙p N∙n∙Ф

Infatti: E = -- ∙ em essendo em = ---- allora: E = --

2·a a

2∙p N

siccome K = -- ∙ -- , allora: E = K ∙ n ∙ Ф

2∙a 60

dove: 2·a è il numero di vie interne e K è una costante dipendente dai poli, dalle vie interne e dal numero di conduttori.

Le macchine a corrente continua derivano tutte dalla classica macchina ad anello di Pacinotti, che, anche se oggi è completamente abbandonata, è didatticamente utile per spiegare il principio di funzionamento.

In basso è raffigurata la macchina con l'anello di Pacinotti:

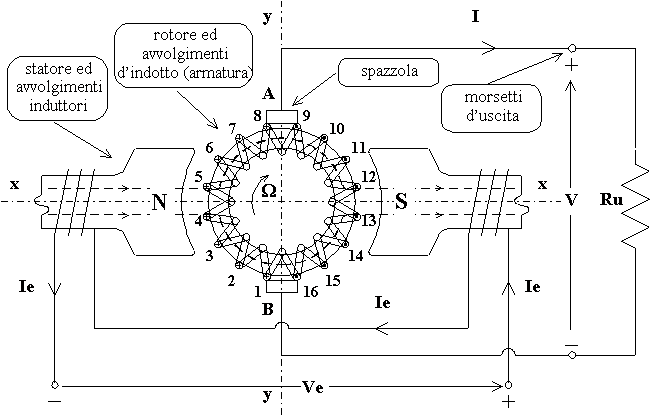
Questa macchina, ideata da Antonio Pacinotti più di un secolo fa, aveva l'indotto del tipo ad anello. L'anello era costituito da materiale di ferro lamellato sul quale era avvolto a spire serrate, un conduttore di rame isolato, che costituiva un circuito chiuso (avvolgimento indotto); le spire dell'avvolgimento indotto erano collegate elettricamente con le lamelle del collettore, sul quale poggiavano in una posizione ben determinata due spazzole fisse, che collegavano il circuito esterno con l'avvolgimento indotto della macchina.

Questo tipo di indotto ad anello, oggi, è stato completamente abbandonato e sostituito dall'indotto a tamburo dentato principalmente per due ragioni costruttive di seguito illustrate.

La struttura meccanica del tamburo è più robusta di quella ad anello; il tamburo consente la costruzione delle matasse dell'avvolgimento a parte, semplificando così la costruzione dell'avvolgimento indotto. I conduttori attivi degli indotti a tamburo sono sistemati nelle cave, in pratica sulla superficie esterna del tamburo parallelamente all'asse della macchina mediante connessioni frontali in maniera da costituire un circuito chiuso; le cave degli indotti a tamburo sono del tipo aperte consentendo così l'esecuzione a parte delle matasse di avvolgimento e migliorando anche la commutazione.

Dal punto di vista elettrico: negli indotti a tamburo ogni spira ha due conduttori attivi e ciò comporta un'economia del rame d'indotto e minori perdite elettriche nel rame d'indotto. Negli indotti a tamburo si ha pure il vantaggio che, a parità di conduttori attivi, il numero di lamelle del collettore è metà di quello degli indotti ad anello.

Avvolgimento embricato & avvolgimento ondulato

I conduttori attivi delle macchine a corrente continua, sistemati nelle cave d'indotto, sono collegati fra di loro mediante le connessioni frontali anteriori e posteriori in maniera da costituire un circuito chiuso e sono collegati con le lamelle del collettore in modo da determinare fra le spazzole di polarità opposta una tensione praticamente continua.

La distanza angolare fra i conduttori attivi, direttamente collegati fra di loro, è pertanto poco diversa dal passo polare della macchina. Il collegamento dei conduttori attivi si può effettuare in due modi diversi:

Avvolgimento embricato

Avvolgimento ondulato

Nell'avvolgimento embricato:

Si hanno tante spazzole quanti sono i poli, le quali (equidistanti fra loro) si succedono con polarità alternativamente positive e negative;

Le spazzole dividono l'avvolgimento in tante vie interne quanti sono i poli; ogni via interna comprende perciò un numero di conduttori pari al numero totale dei conduttori indotti diviso per il numero di poli; questi conduttori si trovano metà sotto un polo e l'altra metà sotto il polo seguente;

Le spazzole dello stesso nome sono collegate tutte fra loro a costituire rispettivamente i due morsetti positivo e negativo della macchina dai quali si deriva il circuito esterno; a tali morsetti fanno capo le vie interne, fra loro in parallelo;

La tensione che si rende disponibile fra i morsetti, positivo e negativo, corrisponde pertanto a quella che si genera in ciascuna via interna ;

La corrente nel circuito esterno è fornita in parti uguali da ciascuna via interna , e perciò i conduttori dell'avvolgimento sono percorsi da una corrente pari a quella del circuito esterno divisa per il numero di poli;

Le connessioni al collettore sono tali che partendo da una lamella e seguendo l'avvolgimento si arriva alla lamella vicina dopo aver percorso una sola spira.

Questo tipo di avvolgimento è adatto per quei generatori che sono destinati a fornire una corrente di elevata intensità ed una tensione relativamente bassa.

Nell'avvolgimento ondulato:

Qualunque sia il numero di poli sono necessarie due sole spazzole, una positiva e una negativa, le quali appoggiano sul collettore in corrispondenza di due poli di nome contrario.

Le due spazzole dividono l'avvolgimento chiuso in due vie interne ognuna delle quali comprende metà dei conduttori dell'indotto;

La tensione che si rende disponibile fra le spazzole corrisponde perciò a quella che si genera in metà dei conduttori indotti;

La corrente nel circuito esterno è fornita in parti eguali dai due circuiti interni connessi fra loro in parallelo e perciò è doppia di quella che percorre i conduttori dell'avvolgimento;

Le connessioni al collettore sono tali che partendo da una lamella e seguendo l'avvolgimento si arriva alla lamella vicina dopo aver fatto un giro completo intorno all'indotto, percorrendo un conduttore per ogni polo.

Questo tipo di avvolgimento, diversamente a quello di prima, è adatto per una corrente limitata e una tensione piuttosto elevata.

Funzionamento a vuoto della dinamo

La dinamo si dice funzionante a vuoto quando, con l'induttore eccitato con la corrente Ie [A] e l'indotto trascinato in rotazione a velocità costante n [g/1'] , Ω [rad/s], ha i morsetti d'uscita aperti, ovvero I = 0, Ru = . In tali condizioni è nulla anche la corrente nelle vie interne e l'unico flusso presente nella macchina è quello induttore principale Φ₀ [Wb].

La f.e.m. che si raccoglie tra le spazzole ha l'espressione seguente:

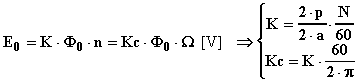
dove N è il numero totale dei conduttori attivi d'armatura e dove [rad/s] è la velocità angolare del rotore. Se nulla viene detto al riguardo, si pone sempre 2·a = 2·p. Solo se si specifica che l'indotto ha l'avvolgimento ondulato si porrà 2·a = 2 indipendentemente dal numero di poli (ricordiamo che l'avvolgimento ondulato è usato per dinamo che generano elevate tensioni e piccole correnti; se si desidera generare piccole tensioni ma elevate correnti si usa l'avvolgimento embricato).

Si osserva come la f.e.m. a vuoto (e quindi anche la tensione d'uscita a vuoto) sia direttamente proporzionale al flusso per polo ed alla velocità. Variando l'una o l'altra di queste due grandezze è possibile variare la tensione d'uscita della dinamo. E' possibile tracciare la caratteristica di magnetizzazione o a vuoto Eo = f(Ie) della dinamo a velocità costante.

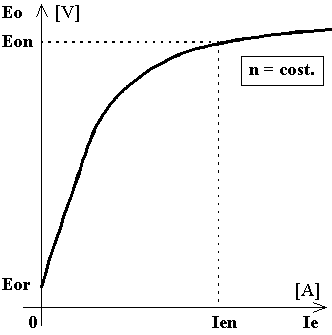
L'andamento di tale caratteristica è quello tipico dei materiali ferromagnetici, la corrente di eccitazione è proporzionale al campo magnetico, la f.e.m. è proporzionale al flusso e quindi all'induzione. Infatti:

N ∙ Ie ∙ N ∙ Ie ∙ N ∙ Ie ∙ S

H = --- e B =μ· H = ---- allora Φ = B ∙ S = -----

l l l

dove: H è l'intensità del campo magnetico [Aspire/m]; è la permeabilità magnetica[H/m]; S è la superficie[m²].

Si osserva che, a causa del magnetismo residuo dei poli, tipico nelle macchine eccitate in corrente continua, si ha una f.e.m. Eor anche con corrente di eccitazione nulla.

Reazione d'indotto della dinamo

E' detta anche "reazione d'armatura" ed è il complesso dei fenomeni che si manifesta quando alla dinamo, eccitata e trascinata in rotazione, è applicata una resistenza di carico Ru [Ω]. In tali condizioni la dinamo eroga corrente continua I [A] ed anche nelle sue vie interne circolerà corrente ( pari ad I/2 se le vie interne sono due).

Quando la dinamo eroga corrente a un circuito esterno anche gli avvolgimenti indotti vengono attraversati da corrente alternata e producono perciò essi stessi un campo magnetico che viene denominato "campo di indotto" H_I o "campo trasverso" (generato dalla corrente circolante nelle vie interne) che si sovrappone al campo magnetico induttore principale H₀ in quanto si affaccia anch'esso sulle sponde del traferro; il flusso di reazione, se le spazzole della macchina si trovano sul piano neutro primitivo(y,y), si chiude attraverso i poli della macchina e crea sull'indotto due poli, detti poli indotti di reazione N', S' aventi l'asse normale dei poli induttori.

Il campo trasverso provocherà degli effetti:

a)  L'effetto principale prodotto dal campo è l'alterazione che esso imprime al campo induttore della dinamo. I due campi si compongono fra loro a formare un campo risultante unico H in cui alle estremità delle espansioni polari si creano dei corni polari d'entrata e di uscita. In questo modo il campo trasversale tende a rinforzare il campo induttore nei corni polari di uscita e tende invece a indebolirlo nei corni polari d'entrata.

b)  Il campo risultante appare così distorto nel senso del movimento. La distribuzione del flusso attraverso i poli e l'armatura risulta in tal modo disuniforme, crescendo da un corno polare all'altro nel senso della rotazione: è questo il fenomeno della distorsione del campo risultante, chiamato anche "effetto torcente della corrente d'armatura".

c)  Nel passaggio da vuoto a carico della dinamo, il piano di inversione del campo viene a spostarsi nel verso del moto dalla posizione y,y alla nuova posizione y',y' di un angolo β; la quale determina la posizione da assegnare alle spazzole.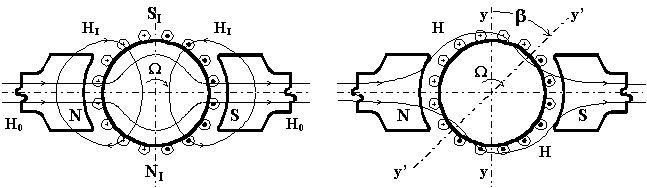

d)  Se le spazzole vengono spostate nel senso della rotazione, la reazione di indotto si manifesta, oltre che con un effetto torcente dovuto al campo trasversale, anche con un effetto smagnetizzante dovuto al campo di indotto; il quale ne risulta tanto più indebolito quanto maggiore è l'angolo β di spostamento delle spazzole, perché il numero di amperspire smagnetizzanti aumenta proporzionalmente all'angolo 2∙ β.(questo effetto complessivo smagnetizzante si ha perché l'indebolimento nei corni polari d'entrata prevale sul rafforzamento dei corni polari di uscita). 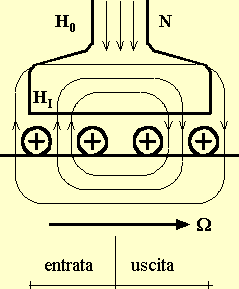(con riferimento alla figura si osserva che le linee di induzione del campo magnetico induttore H₀ sono dirette verso il basso, mentre quelle del campo magnetico d'indotto H_I vanno verso l'alto nella zona d'entrata e verso il basso nella zona d'uscita della scarpa polare. Il campo magnetico complessivo sarà allora indebolito in entrata e rafforzato in uscita ). Dal grafico della caratteristica di magnetizzazione,inoltre,si nota che se il ferro è lontano dalla saturazione, alle due variazioni del campo corrispondono in modo proporzionale due variazioni di induzione così che il flusso complessivo del polo rimane invariato. Se il ferro è in saturazione, alla diminuzione del campo corrisponde una proporzionale diminuzione dell'induzione mentre all'aumento del campo corrisponde un aumento piccolissimo di induzione così che il flusso complessivo per polo diminuisce e con esso cala la f.e.m. indotta.

e)  Quando le spazzole sono spostate nel senso della rotazione si ha pertanto una sensibile diminuzione del flusso totale nell'intraferro e quindi una diminuzione della f.e.m. generata dalla macchina. Ne consegue che la differenza fra la f.e.m. generata a vuoto E₀ e la f.e.m. E generata a pari corrente di eccitazione e pari velocità ma sottocarico costituisce la caduta di f.e.m. per reazione d'indotto che assume l'espressione: ∆E = E₀ - E [V]. Se si vuole compensare la caduta di tensione per reazione d'indotto si dovrà convenientemente aumentare la corrente di eccitazione. Nelle macchine sature (cioè col circuito magnetico che si trova a lavorare in saturazione, od almeno nel ginocchio che la precede) si verifica inoltre una riduzione del flusso per polo e, quindi, una maggior caduta di f.e.m. nel passaggio da vuoto a carico.

f)    Quando la dinamo passa da vuoto a carico, come già si è visto, si creano dei poli d'indotto N', S' che si trovano spostati arretrati (con riferimento al senso di rotazione dell'indotto) di mezzo passo polare rispetto agli omonimi poli induttori. E' evidente che tra i poli induttori ed i poli d'indotto scaturiscono delle forze che, come è facile verificare, danno origine ad una coppia elettromagnetica frenante (o una coppia resistente) che si oppone alla rotazione dell'indotto. Quindi, per mantenere in rotazione l'indotto, si dovrà applicare una coppia motrice C, attraverso il motore primo, che trascina l'indotto stesso e si dovrà spendere una potenza meccanica Pa = Ω · C [W] che, a meno delle perdite, verrà erogata al carico sotto forma elettrica.

Coppia elettromagnetica frenante nella dinamo

Abbiamo già visto come, nel caso della dinamo sotto carico, la corrente presente nelle vie interne origina dei poli d'indotto che interagiscono coi poli induttori determinando una coppia elettro-magnetica frenante.

Se E [V] è la f.e.m. presente tra le spazzole ed Ii [A] è la corrente erogata dalle spazzole (chiamata anche corrente d'indotto), sicuramente E · Ii [W] è la potenza elettrica generata dalla dinamo. A meno delle perdite meccaniche e nel ferro, E · Ii [W] rappresenta anche la potenza meccanica che il motore primo fornisce alla dinamo, inoltre essendo Ω [rad/s] la velocità di rotazione dell'albero coassiale si avrà che tale motore dovrà erogare una coppia:

Pl = Pa (per il principio di conservazione dell'energia la potenza elettrica è

uguale a quella meccanica spesa per mantenere in rotazione il rotore)

E · I = Ω ·C

2 · π · n 2·p N

K · n · · I = --- ·C   => C = -- · - · · I => C = K'· · I [Nm]

2·a 2·

2·p N

con K' = -- · -

2·a 2·π

In condizioni di equilibrio dinamico, questa è ovviamente anche la coppia elettromagnetica frenante originata dalla dinamo quando essa eroga corrente.  

La commutazione nella dinamo

Nelle macchine a corrente continua, essendo i poli induttori fissi nello spazio, anche i poli indotti di reazione restano fissi nello spazio, al contrario di ciò che avviene nelle macchine asincrone e sincrone; anche la configurazione delle correnti, che circolano nei conduttori d'indotto, resta quindi fissa nello spazio. Poiché l'avvolgimento indotto della macchina è costituito da 2·a rami d'indotto, percorsi alternativamente da correnti nei due sensi, si ha che ogni conduttore d'indotto durante la rotazione della macchina passa successivamente da un ramo all'altro d'indotto, invertendo ad ogni passaggio il senso della corrente che circola in esso.

La commutazione è l'insieme dei fenomeni che si verificano nella dinamo quando funziona sottocarico e dovuti al fatto che la corrente, nella spira in commutazione, compresa fra due lamelle in transito, sotto le due spazzole, si inverta.

All'atto della commutazione si ha che la corrente I_C [A] nel conduttore cambia verso e il contatto strisciante tra spazzola e lamelle del collettore viene sottoposto ad importanti sollecitazioni termiche.

La commutazione, come ci fa capire il diagramma seguente può essere di tipo lineare (è una commutazione teorica e rappresenta una buona commutazione - come dovrebbe accadere) e di tipo reale (è la vera commutazione - quello che in effetti accade)

Nel caso lineare (ideale), trascurando tutte le f.e.m. indotte nella spira che sta commutando, trascurando la resistenza dei conduttori che costituiscono la spira stessa, considerando la sola resistenza del contatto spazzola-lamella e supponendo tale resistenza inversamente proporzionale alla superficie di contatto, accade che la corrente nel conduttore in commutazione varia linearmente durante il tempo T [s] di commutazione e la densità di corrente rimane costante su tutta la superficie del contatto.

Nel caso reale accade che:

a) la spira (che oltre ad essere in corto circuito è anche immersa nel ferro quindi ha una sua induttanza L) durante la commutazione è soggetta ad una variazione di corrente nel tempo (passando da una via interna all'altra la corrente nel conduttore si inverte) che scaturisce una f.e.m. di autoinduzione (o f.e.m. di commutazione) a causa dell'induttanza propria della spira che, per la legge di Lenz, si oppone all'inversione della corrente;

ΔΦ ( la f.e.m. indotta agisce nella spira in modo tale da impedire

e = - L -- ovvero ritardare l'inversione della corrente)

Δ t

La f.e.m. indotta risulta massima nell'ultimo istante di commutazione quando la spazzola sta per abbandonare una lamella del collettore, essendo massima la variazione di corrente nella sezione. La densità di corrente elevata sotto il bordo della spazzola, che sta per abbandonare una lamella del collettore, crea una sopraelevazione di tensione fra spazzola e lamella tale da vincere la rigidità dielettrica RD dell'aria quindi favorisce la formazione di un arco elettrico (scintilla).

b) La distorsione del campo magnetico dovuta alla reazione d'indotto fa sì che la spira in commutazione si trovi, all'atto della commutazione, ancora sotto l'influenza del polo di provenienza e, quindi, interessata da una f.e.m. concorde con quella che si aveva prima della commutazione, la quale ostacola l'inversione della corrente.

Il risultato complessivo sarà quello di produrre nel conduttore in commutazione una variazione della corrente non più lineare durante il tempo T. A causa di questo si manifestano due gravi inconvenienti:

1) la densità di corrente sotto le spazzole non è più costante, più precisamente è maggiore nella zona d'uscita della spazzola. Tale zona subirà quindi un maggiore riscaldamento con una conseguente maggiore usura;

2) tra la spazzola e la lamella che sta per essere abbandonata dalla spazzola si stabilisce una elevata d.d.p. e, di conseguenza, può scoccare una scintilla tra la spazzola e la lamella nell'istante del distacco (tale fenomeno viene favorito dall'elevata temperatura della spazzola, di cui al punto a), e dalle condizioni impure dell'aria circostante il collettore per la presenza di un pulviscolo derivante dal consumo delle spazzole).

Il frequente verificarsi degli inconvenienti a) e b) produce una rapida usura delle spazzole e del collettore a lamelle.

Per ridurre gli aspetti negativi conseguenti alla commutazione si può:

a) aumentare la resistenza della spira in commutazione e ridurre i flussi dispersi nell'indotto (ovvero ridurre l'induttanza della spira). In tal modo si riduce la costante di tempo τ = L / R [s] del transitorio di commutazione e la situazione di regime viene raggiunta in un tempo più breve. Per aumentare la resistenza della spira si adottano spazzole a base di grafite (conduttore non Ohmico) ad elevata caduta di tensione;

b) realizzare matasse di poche spire e calate in cave aperte (in tal modo i flussi dispersi si riducono a causa dell'elevata riluttanza che essi incontrano nell'aria) così che sia piccola la f.e.m. autoindotta che si oppone all'inversione della corrente;

c) realizzare l'induttore nella forma a poli sporgenti, così che la commutazione avvenga in una zona ad elevato traferro e, quindi, ad elevata riluttanza del circuito magnetico. In tal modo saranno più bassi i valori di induzione del flusso tagliato dalla spira prossima alla commutazione e, con ciò, più basse saranno le f.e.m. indotte che si oppongono all'inversione della corrente nella spira.

Avvolgimenti compensatori e poli ausiliari nella dinamo

Avvolgimenti compensatori.

Vengono utilizzati per ridurre gli effetti negativi della reazione d'indotto. Consistono in conduttori inseriti in opportuni canali (paralleli alla generatrice del cilindro dell'indotto) ricavati nelle scarpe polari induttrici. Tali conduttori devono essere percorsi da una corrente continua con verso opposto ed intensità proporzionale a quella ( Ia ) che si ha nella via interna sottostante il polo. Tali avvolgimenti sono posti in serie alle spazzole e quindi sono percorsi dalla corrente ( I ) erogata al carico. Il campo magnetico da loro generato si oppone al campo d'indotto riducendone gli effetti negativi.

La figura sottostante mostra, per una dinamo a quattro poli, la disposizione degli avvolgimenti compensatori e dei poli ausiliari (dei quali parleremo tra breve):

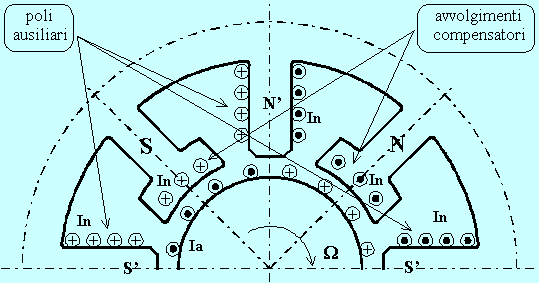
E' possibile dimensionare il numero di conduttori compensatori Nc da porre in ciascun polo. Indicando con In [A] la corrente nominale erogata dalla macchina, Ia [A] la corrente in ciascuna via interna, Pn [W] la potenza nominale (potenza elettrica erogata), Vn [V] la tensione nominale d'uscita, Cc% la porzione dell'intera circonferenza d'indotto coperta dalle espansioni polari espressa in percento, N il numero totale di conduttori d'indotto, Np il numero di conduttori d'indotto sotto un singolo polo, 2·a il numero di vie interne, si ha:

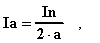
Infine, imponendo l'eguaglianza tra la f.m.m. d'indotto e la f.m.m. compensatrice si ha:

Essi hanno il compito di contrastare l'effetto di distorsione della reazione d'indotto, quindi di annullare, al traferro, il campo trasverso per cui essi devono produrre un campo in ogni momento uguale e contrario a quello trasverso.

Poli ausiliari.

L'impiego degli avvolgimenti compensatori, riducendo la distorsione del flusso che si ha a carico, favorisce pure una migliore commutazione. Un deciso miglioramento della commutazione si ha attraverso l'impiego dei poli ausiliari. Tali poli sono di sezione più piccola dei poli principali e non hanno espansione polare; essi vengono posti nei vani interpolari, quindi sull'asse interpolare ove avviene la commutazione, e sono tali da indurre nelle spire in commutazione una f.e.m. che si oppone a quelle che ostacolano la commutazione stessa. Per ottenere ciò occorre che abbiano la polarità del polo verso il quale vanno i conduttori in commutazione e che la corrente negli avvolgimenti che li eccitano sia quella ( I ) erogata dalla dinamo (quindi tali avvolgimenti, come quelli compensatori, devono essere in serie alle spazzole).

Per le piccole macchine a corrente continua talvolta i canali aperti e lo spostamento delle spazzole secondo il piano di inversione reale sono sufficienti a contenere il fenomeno.

Se ci sono i poli ausiliari le spazzole sono disposte secondo il piano di inversione ideale.

Dinamo con eccitazione indipendente

Ha il seguente schema elettrico:

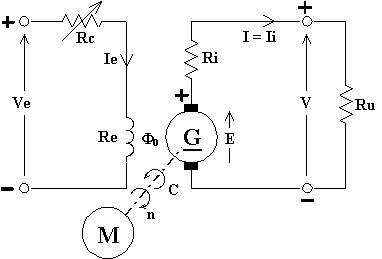
In essa il circuito di eccitazione è totalmente disgiunto dal circuito d'indotto (le piccole dinamo nelle quali il sistema induttore è costituito da un magnete permanente sono riconducibili al medesimo modello).

Nel modello si evidenziano:

a) la tensione Ve [V] e la corrente Ie [A] d'eccitazione.

b) La resistenza del reostato di campo Rc [Ω] che permette, a parità di tensione d'eccitazione, di variare la corrente d'eccitazione e quindi il flusso induttore principale [Wb], coincidente col flusso nella macchina a vuoto.

c) La resistenza degli avvolgimenti induttori Re [Ω]. Per lo studio dei fenomeni transitori è necessario introdurre nel modello anche l'induttanza Le [H] di tale avvolgimento.

d) La f.e.m. E [V] indotta negli avvolgimenti d'armatura. Tale f.e.m. è esprimibile come:

E = K· · n = E₀ - ΔE [V]

dove: è il flusso a carico (minore di quello a vuoto ). La caduta di f.e.m. per reazione d'indotto ΔE non è esprimibile in forma analitica, può essere nota in seguito a prove fatte sulla macchina ed espressa in forma tabellare o grafica. In ogni caso vale qualche percento (circa 5%) a pieno carico.

e) La resistenza interna Ri [Ω]. Si tratta della resistenza complessiva dei conduttori costituenti le varie vie interne (da considerarsi tra di loro in parallelo) dell'indotto, in serie alla resistenza degli eventuali avvolgimenti compensatori, in serie alla resistenza degli avvolgimenti degli eventuali poli ausiliari. Per quanto riguarda la resistenza di contatto delle spazzole, essendo queste di tipo non ohmico, si preferisce considerare la c.d.t. totale dovuta a tale contatto. Essa è convenzionalmente assunta pari a 2 [V] nel caso di spazzole in grafite, 0,6 [V] nel caso di spazzole a contenuto metallico.

Per lo studio dei fenomeni transitori è necessario introdurre nel modello anche l'induttanza Li [H] del circuito costituito dall'indotto della macchina e dal carico ad essa allacciato, oltre al momento d'inerzia complessivo delle masse rotanti.

f) La tensione d'uscita V [V] e la corrente erogata I [A]. Per questo tipo di dinamo, la corrente erogata coincide con la corrente d'indotto Ii [A]. Lo schema disegnato mostra anche la resistenza Ru [Ω] che riassume l'utilizzatore alimentato dalla dinamo.

Il funzionamento a carico della macchina può essere descritto attraverso le seguenti equazioni interne:

E₀ = f (Ie) (caratteristica di magnetizzazione)

E = K· · n = E₀ - ΔE

V = E - Ri · I (caratteristica esterna)

Ve = (Rc + Re) · Ie

C = K'· ·Ii

e l'equazione esterna: V = Ru· I (detta retta di carico).

La caratteristica esterna V = f(I) e la retta di carico V = f'(I) possono pure essere rappresentate graficamente. Se si trascura la ΔE e si assumono costanti la velocità di rotazione e la corrente di eccitazione, le due caratteristiche hanno l'aspetto di figura sotto riportato.

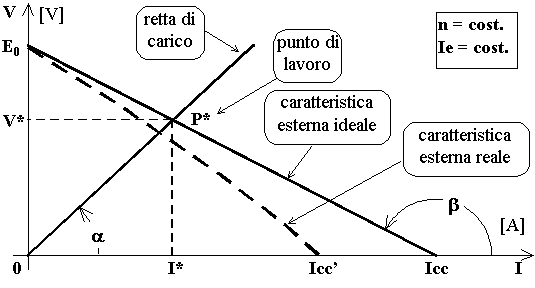
L'intersezione della caratteristica esterna con l'ordinata costituisce il punto di funzionamento a vuoto per il quale Ru = [Ω] , I = 0 [A] , V = E₀ [V] ; mentre l'intersezione con l'ascissa costituisce il punto di funzionamento in cortocircuito per il quale Ru = 0 [Ω] , I = Icc = E₀ / Ri [A] , V = 0 [V]. Inoltre, è facile verificare che è tg(ß) = - Ri , tg(α) = Ru. L'intersezione tra la caratteristica esterna e la retta di carico individua il punto di lavoro del generatore le cui coordinate corrispondono alla corrente ed alla tensione ai morsetti d'uscita per quella determinata retta di carico.

Osservazione: la potenza erogata è nulla a vuoto ed in cortocircuito; invece,assume il valore massimo quando Ru = Ri ed in tal caso vale:

Il rendimento in tali condizioni vale 0,5. Quando si verifica questa condizione si dice che vi è l'adattamento di massima potenza tra generatore e carico.

Osservazione: se si tiene conto della caduta di f.e.m. per reazione d'indotto, la caratteristica esterna risulta essere non più rettilinea (a causa della non linearità del fenomeno) e più cadente, per cui la corrente di cortocircuito Icc' sarà più piccola.

Per variare la tensione d'uscita di una dinamo si può intervenire sulla velocità di rotazione oppure sulla corrente d'eccitazione. Naturalmente risulta più semplice intervenire sulla corrente d'eccitazione. In ogni caso la caratteristica esterna si modifica spostandosi parallelamente a se stessa, infatti sia la f.e.m. a vuoto che la corrente di cortocircuito sono direttamente proporzionali alla velocità ed al flusso (e, quindi, alla corrente d'eccitazione). La caratteristica si alza se aumenta la velocità oppure la corrente d'eccitazione, diversamente si abbassa.

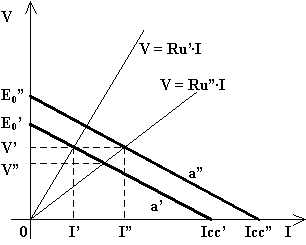
Ad esempio, se abbiamo una dinamo che eroga la corrente I' con tensione d'uscita V' quando la resistenza dell'utilizzatore vale Ru', nel caso in cui la resistenza dell'utilizzatore diventi Ru" < Ru' varierà la tensione d'uscita da V' a V" < V'. Se si desidera mantenere costante la tensione d'uscita, bisognerà aumentare la corrente d'eccitazione (o la velocità di rotazione) in modo tale che la caratteristica esterna si alzi portandosi da a' ad a". Ovviamente assieme alla tensione varierà anche la corrente erogata.

Altre due caratteristiche significative per la dinamo ad eccitazione indipendente sono la caratteristica totale e la caratteristica di regolazione, rispettivamente:

E = f(I) , n = cost. , Ie = cost.

Ie = f(I) , n = cost. , V = cost.

di andamento facilmente immaginabile.

Dinamo ad eccitazione derivata

Ha il seguente schema elettrico:

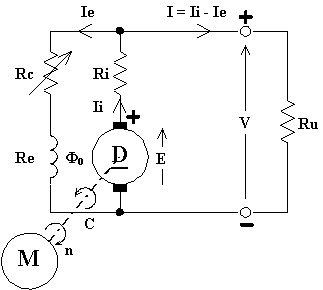
La macchina può funzionare solo se in essa è presente un adeguato magnetismo residuo, solo in tal caso può avere inizio l'autoeccitazione a vuoto. Per tale motivo essa ha un senso di rotazione obbligato, infatti il campo prodotto dall'avvolgimento induttore deve essere concorde col campo originato dal magnetismo residuo.

Nel funzionamento a vuoto é nulla la corrente I erogata verso il carico, quindi si ha una corrente d'indotto coincidente con quella d'eccitazione, Ii = Ie. Tale corrente è sempre piuttosto piccola, per tale motivo risulta trascurabile la reazione d'indotto e si può porre E ≈E₀. Il punto di lavoro nominale Pn sulla caratteristica di magnetizzazione E₀ = f(Ie) viene individuato dall'intersezione della retta E₀ = (Rc + Re + Ri) · Ie con la caratteristica stessa e si situa normalmente dopo il ginocchio. E' fondamentale che il punto di lavoro non cada nel tratto rettilineo della caratteristica di magnetizzazione, infatti, se questo si verificasse, si avrebbero inaccettabili variazioni della tensione d'uscita anche per piccolissime variazioni del valore del reostato di campo Rc. Quindi esiste un punto di lavoro critico P_CR a sinistra del quale non si deve andare e ciò impone un valore massimo alla resistenza complessiva (Rc + Re + Ri):

(Rc + Re + Ri)_CR = R_CR + Ri = tg(α_CR)

Quindi, in sede di progetto, il reostato di campo viene dimensionato in modo tale da non superare, sommato alla resistenza propria degli avvolgimenti d'indotto, il valore R_CR.

Nel funzionamento a carico la macchina risulta descritta dalle seguenti equazioni interne:

E₀ = f (Ie) (caratteristica di magnetizzazione)

E = K· · n = E₀ - ΔE

Ii = I + Ie

V = E - Ri · Ii = E - Ri · (I+Ie) (caratteristica esterna)

Ve = (Rc + Re) · Ie

C = K'· ·Ii

e l'equazione esterna: V = Ru· I (detta retta di carico).

La caratteristica esterna V = f(I) , per resistenza del reostato di campo e velocità di rotazione costanti, ha il primo tratto che non differisce di molto da quello già visto per la dinamo ad eccitazione indipendente, solo che ora si presenta con maggiore pendenza perché la tensione ai morsetti della macchina diminuisce all'aumentare della corrente erogata, oltre che per la reazione d'indotto e la caduta Ohmica sulla resistenza interna, anche perché diminuisce la corrente d'eccitazione cosicché si viene a determinare un ulteriore indebolimento del flusso induttore.

Tale fenomeno aumenta mano a mano che la corrente di carico aumenta d'intensità fino al valore Imax di corrente erogata. Se, raggiunta tale corrente, si diminuisce ulteriormente il valore della resistenza di carico, succede un fenomeno inconsueto: la corrente erogata diminuisce anziché aumentare e la tensione d'uscita si abbassa molto rapidamente fino a diseccitare la macchina. Tutto questo accade perché la corrente di eccitazione è diventata insufficiente a causa del forte abbassamento della tensione d'uscita. Infatti la corrente d'eccitazione è derivata in parallelo dalla tensione d'uscita e la sua diminuzione comporta una diminuzione del flusso e, quindi, della tensione d'uscita stessa: in pratica il fenomeno si esalta portando alla totale diseccitazione della macchina anche se dall'esterno non si è ulteriormente ridotta la resistenza di carico. Quindi il punto P_CR sulla caratteristica esterna individua la retta di carico di pendenza ß_CR che costituisce il limite per la stabilità di funzionamento della dinamo. In definitiva non è possibile ridurre la resistenza del carico ad di sotto del valore R_CR = tg(ß_CR).

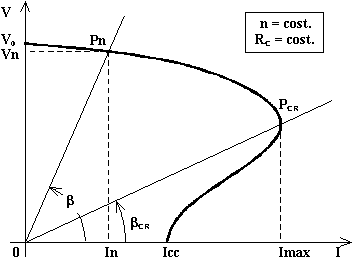
Si può affermare che il funzionamento della dinamo è stabile nel tratto di curva che va dal punto di funzionamento a vuoto (Ru = , I = 0,V = V₀) al punto P_CR, mentre è instabile nel tratto che va da P_CR al punto di funzionamento in cortocircuito (Ru = 0, I = Icc, V = 0). In una macchina correttamente dimensionata il punto nominale di funzionamento si colloca come Pn in figura.

La corrente di cortocircuito Icc risulta essere sensibilmente inferiore rispetto quella che si ha in un'analoga macchina ad eccitazione indipendente, tuttavia è (di solito) significativamente maggiore della corrente nominale e, per tale motivo, anche in questo generatore è da temere (ed evitare) il funzionamento in cortocircuito.

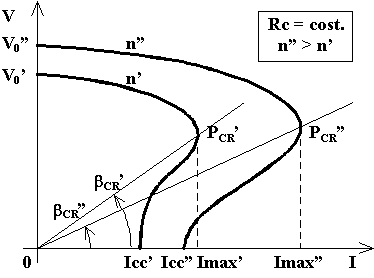
Al variare del numero di giri la caratteristica esterna cambia secondo le modalità rappresentate in figura. Cambiando la caratteristica cambia anche il valore di R_CR, più precisamente si verifica che ad una diminuzione del numero di giri corrisponde un aumento di R_CR.

Un'altra caratteristica significativa per la dinamo ad eccitazione derivata è la caratteristica di regolazione, del tutto analoga a quella già vista per la dinamo ad ecc. indipendente.

Riassumendo, le dinamo con eccitazione derivata sono di più facile installazione delle dinamo ad eccitazione indipendente non richiedendo alcuna rete ausiliaria in corrente continua per l'eccitazione. La loro caratteristica esterna (a parità di numero di giri) ha maggior pendenza rispetto alle dinamo con eccitazione indipendente ma col reostato di campo si può facilmente compensare questo inconveniente. L'inconveniente maggiore è quello di presentare un valore di resistenza di carico R_CR al di sotto del quale non è possibile andare e che nemmeno risulta avvicinabile essendo eccessivamente grande la corrente altrimenti erogata dalla macchina. Inoltre, come già detto, hanno un verso obbligato di rotazione.

Dinamo ad eccitazione serie

Ha il seguente schema elettrico:

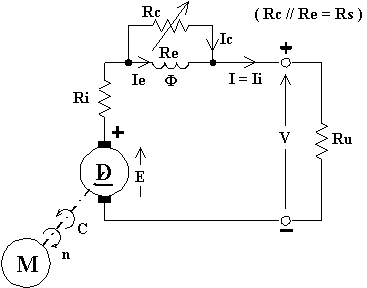
La macchina può funzionare solo se in essa è presente un adeguato magnetismo residuo, solo in tal caso può avere inizio l'autoeccitazione. Per tale motivo essa ha un senso di rotazione obbligato, infatti il campo prodotto dall'avvolgimento induttore deve essere concorde col campo originato dal magnetismo residuo. L'azione del reostato è in senso contrario rispetto ai casi precedenti, infatti per ridurre la tensione occorre diminuire Rc in modo tale che diminuisca Ie, viceversa per aumentare la tensione.

Nel funzionamento a carico la macchina risulta descritta dalle seguenti equazioni interne:

E₀ = f (Ie) (caratteristica di magnetizzazione)

E = K· · n = E₀ - ΔE

V = E - (Ri + Rs) · I = E₀ - ΔE - (Ri + Rs) · I (caratteristica esterna)

C = K'· ·Ii

Rc

Ie = I · ---- , se Rc = si ha Ie =I

Re + Rc

e l'equazione esterna: V = Ru· I (detta retta di carico).

Quindi, per velocità di rotazione e reostato di campo costanti, la caratteristica esterna può essere determinata detraendo dalla E₀ la caduta per reazione d'indotto ΔE e la caduta sulla resistenza interna e sugli avvolgimenti eccitatori (con eventuale reostato di campo in parallelo):

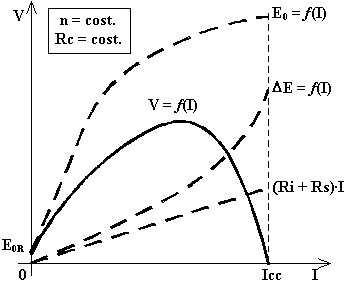
Al crescere della corrente erogata (cioè al variare della resistenza di carico da infinito a zero) cresce anche la corrente di eccitazione e, quindi, E₀ e, con essa, la tensione d'uscita V. Tuttavia, a causa del fenomeno di saturazione, la E₀ cresce sempre meno mentre la caduta per reazione d'indotto ΔE cresce sempre di più: prima o poi la tensione d'uscita comincerà a calare per ridursi a zero in cortocircuito.

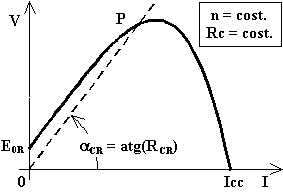
Anche per questa dinamo si può parlare di un valore critico R_CR della resistenza di carico. Infatti all'aumentare della resistenza di carico, la retta di carico aumenta la propria pendenza fino a diventare pressoché parallela al primo tratto della caratteristica esterna. In tali condizioni basta una piccola variazione della resistenza di carico per avere una forte variazione sia della tensione d'uscita che della corrente erogata e questo fatto è indesiderato. Quindi è bene che sia Ru << R_CR.

Vengono chiamate dinamo a corrente costante quelle dinamo costruite per avere una elevata caduta interna per reazione d'indotto ΔE. Per tali dinamo la caratteristica esterna ha il tratto finale decrescente praticamente verticale: utilizzando la macchina in questo tratto della sua caratteristica esterna si avrà l'erogazione di una corrente (prossima a quella di cortocircuito) costante ed indipendente dalla tensione d'uscita.

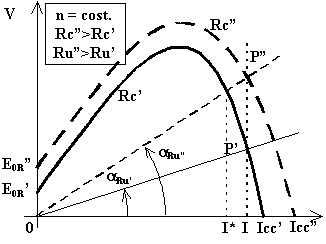
Negli impianti utilizzanti dinamo con eccitazione in serie è importante mantenere costante la corrente erogata al carico anche quando la resistenza del carico medesimo varia. Ad esempio, se la resistenza del carico aumenta da Ru' a Ru", a parità di velocità e di reostato di campo, si avrà una diminuzione della corrente erogata da I a I*. Per mantenere costante e pari ad I la corrente erogata si dovrà aumentare da Rc' a Rc" il valore del reostato di campo in modo tale da aumentare il flusso e, con esso, sia la tensione d'uscita che la corrente erogata.

Per le dinamo con eccitazione in serie la caratteristica di regolazione viene definita diversamente, più precisamente essa è il grafico della corrente di eccitazione in funzione della tensione d'uscita per valori costanti di velocità e corrente erogata.

Dinamo ad eccitazione composta

Ha il seguente schema elettrico:

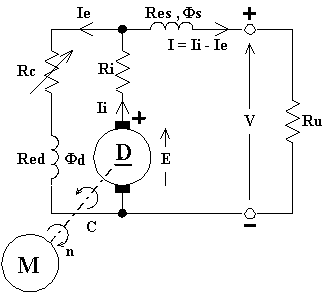
Su ciascun polo induttore della dinamo vengono poste due bobine anziché una, la prima Red composta di molte spire di piccola sezione eccitata in derivazione, la seconda Res composta di poche spire di grande sezione eccitata in serie. Tale tipo di eccitazione si può ottenere in due modi, a corta derivazione (come in figura) o a lunga derivazione.

Le equazioni interne e l'equazione esterna sono analoghe a quelle già viste per le altre dinamo e si ricavano dal circuito equivalente sopra disegnato.

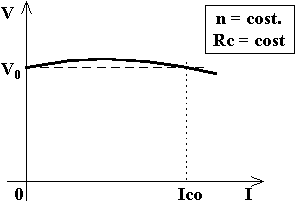
Per quanto riguarda la caratteristica esterna, siccome per le dinamo in derivazione essa è calante mentre per le dinamo in serie essa è nel primo tratto crescente, dimensionando opportunamente il numero di spire degli avvolgimenti d'eccitazione in derivazione ed in serie si riesce a far si che la caratteristica esterna sia praticamente costante nel primo tratto. Viene chiamata corrente di compensazione quella corrente erogata per la quale la tensione d'uscita a carico è uguale alla tensione d'uscita a vuoto. Se In = Ico la dinamo si dice compensata a pieno carico, se In = 2·Ico si dice compensata a metà carico.

La caratteristica di regolazione è del tutto analoga a quella già vista per le altre dinamo.

Perdite e rendimento nella dinamo

Le perdite che si hanno in una dinamo sono:

Pm , perdite meccaniche per attrito e ventilazione;

Pfe , perdite nel ferro a vuoto, localizzate nell'indotto interessato da un flusso variabile e nelle   testate delle espansioni polari induttrici interessate dal fenomeno di pennellamento delle linee di campo magnetico;

Pec , perdite per eccitazione, dovute all'effetto Joule negli avvolgimenti induttori e nel reostato di campo Pec = (Re + Rc)·Ie² ;

Pj , perdite d'indotto, dovute all'effetto Joule negli avvolgimenti d'indotto, compresi gli avvolgimenti compensatori e gli avvolgimenti dei poli ausiliari Pj = Ri·Ii² ;

Ps , perdite nelle spazzole, di tipo non Ohmico essendo le spazzole conduttori non Ohmici. Le norme CEI impongono di calcolarle convenzionalmente, qualunque sia il numero di spazzole, con Ps = 2·Ii [W] per spazzole di grafite, Ps = 0,6·Ii [W] per spazzole a contenuto metallico, dove la corrente è in [A];

Padd, perdite addizionali, sono perdite nel ferro dell'indotto che si aggiungono a quelle che si hanno a vuoto e sono causate dalla distorsione per reazione d'indotto del flusso a carico. Le norme CEI impongono di calcolarle nelle condizioni nominali come l'1% della potenza nominale erogata e di considerarle, per diverse condizioni di carico, variabili col quadrato della corrente erogata.

Si definisce rendimento:

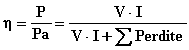dove V·I è la potenza erogata o resa P.

Per una dinamo è poi significativa la variazione di tensione percentuale da carico a vuoto calcolata con:

dove Vn è la tensione nominale, Von è la tensione a vuoto ai morsetti d'uscita quando, a partire dalle condizioni nominali, si interrompe il carico mantenendo costanti la velocità ed il reostato di campo.

MOTORI IN CORRENTE CONTINUA

Generalità e principio di funzionamento

La stessa macchina, con corrente d'eccitazione e polarità delle spazzole identiche, ruota nello stesso senso sia come motore che come generatore, solo che quando funziona come motore cambia il senso della corrente nell'indotto e nelle vie interne così che la f.e.m. E è da intendersi come forza controelettromotrice (f.c.e.m.), e la coppia elettromagnetica generata C (dovuta all'interazione tra il campo magnetico induttore e la corrente nelle vie interne, che origina le due forze F tangenti al cilindro d'indotto) è da intendersi come coppia motrice essendo concorde col verso di rotazione.

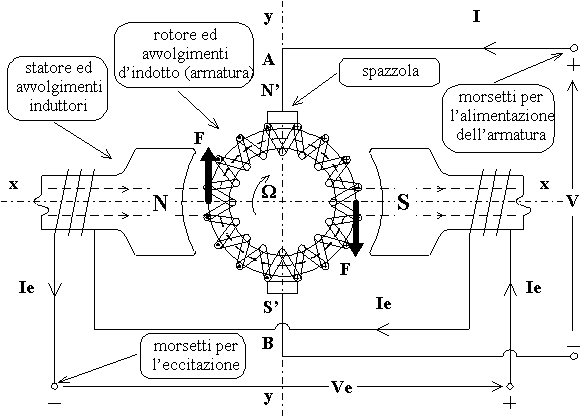
Mentre per i generatori autoeccitati si ha un verso obbligato di rotazione dovuto alla necessità di sfruttare il magnetismo residuo, nei motori autoeccitati ciò non è più vero in quanto il flusso d'eccitazione è originato dalla corrente derivata dalla linea di alimentazione stessa che si trova, sempre, alla tensione V.

La reazione d'indotto si presenta nei motori in forma del tutto analoga a quanto visto per i generatori, solo che l'asse neutro si trova ad essere spostato in anticipo rispetto all'interasse polare. Anche la commutazione si presenta con le stesse proprietà già viste per i generatori. I rimedi tesi a ridurre i problemi dovuti alla reazione d'indotto (avvolgimenti compensatori) ed a facilitare la commutazione (poli ausiliari) già discussi per i generatori rimangono validi anche per i motori, tanto è vero che per una macchina, predisposta per funzionare come generatore, nel caso si intenda impiegarla come motore non è necessario alcun ritocco nei collegamenti degli avvolgimenti compensatori e nei collegamenti degli avvolgimenti dei poli ausiliari. E' facile verificare che la corrente negli avvolgimenti compensatori è senz'altro opposta a quella nella via interna sottostante il polo interessato, mentre l'eccitazione del polo ausiliario è tale per cui esso assume la stessa polarità del polo induttore dal quale la spira commutante proviene, così come deve essere per i motori.

Principio di funzionamento

Quando il motore viene alimentato con tensione V i conduttori dell'avvolgimento indotto sono percorsi da corrente ma sono anche immersi nel campo magnetico induttore; allora, per reazione fra campo magnetico e corrente, su ciascuno di essi nasce una forza elettromagnetica F = B ∙ l ∙ I

La risultante di tutte le forze di destra e la risultante di tutte quelle di sinistra forma una coppia motrice C = Fr ∙ b (ove b è il braccio ed è la minima distanza tra le direzioni delle due forze) che mette in rotazione il rotore.

Una volta in rotazione, i conduttori tagliano le linee di forza del campo e diventano sede di f.e.m. indotte che in totale danno come risultato una f.e.m. E che per legge di Lenz si oppone alla causa che l'ha generata, cioè alla tensione V di alimentazione per cui viene chiamata forza controelettromotrice (f.c.e.m.)

2∙p N

E = K ∙ n ∙ Φ [v] con K = -- ∙ --

2∙a 60

Durante la rotazione poiché si genera una f.c.e.m., è chiaro che per far passare nell'indotto stesso la corrente I, necessaria a mantenerlo in rotazione, si dovrà applicare alle spazzole una tensione V tale da vincere la f.c.e.m. E ed, inoltre, compensare la caduta ohmica Ri ∙ I dovuta alla resistenza propria dell'indotto Ri (comprensiva dell'eventuale resistenza dei vari avvolgimenti posti in serie all'indotto).

La tensione V da applicare alle spazzole di un motore a corrente continua resta perciò determinata dalla relazione fondamentale: V = E + Ri ∙ Ii

Da questa relazione si ricava che la corrente assorbita dall'indotto di un motore è data da:

V - E V - K· n · Φ

I = --- = ------ [A]

Ri Ri

Ne segue che se la tensione V applicata alle spazzole viene mantenuta costante, essendo costante anche la resistenza di indotto Ri, la corrente assorbita dall'indotto può variare solo se varia la f.c.e.m. E; e, precisamente, la corrente aumenterà se la f.c.e.m. diminuisce, viceversa la corrente verrà a diminuire se la f.c.e.m. aumenta.

Il motore, come nella dinamo, ha diversi tipi di eccitazione.

Il motore ad eccitazione indipendente, se si alimenta con le stesse polarità della dinamo, ruota nello stesso senso della dinamo. Per fargli cambiare verso di rotazione, bisogna invertire la polarità dell'armatura o la polarità dell'eccitazione.

Il motore ad eccitazione derivata, comunque lo si alimenti, ruota sempre nello stesso senso della dinamo. Per fargli cambiare verso di rotazione, bisogna invertire il verso della corrente di eccitazione o d'indotto e questo è possibile solo scambiando il morsetto d'inizio con quello di fine di uno solo dei due avvolgimenti.

Il motore ad eccitazione serie, comunque lo si alimenti, ruota sempre in senso contrario a quello che assume funzionando da dinamo. Per fargli cambiare verso di rotazione si deve operare come per il motore con eccitazione derivata.

Il motore ad eccitazione composta, dato che viene costruito in modo tale che l'eccitazione derivata prevalga su quella serie, si comporta come il motore con eccitazione derivata.

Avviamento dei motori a corrente continua

All'atto dell'avviamento è chiaro che quando l'indotto di un motore è fermo la f.c.e.m. è nulla qualunque sia il tipo di eccitazione. In questo istante essendo nulla la f.c.e.m. E, l'indotto si comporta come una semplice resistenza e quindi assorbe una corrente, denominata corrente di avviamento o di spunto Ia, la quale risulta del valore:

V - E

I = --- siccome E = K· n · Φ

V Ri

Ia = -- [A] perché :

Ri e all'avviamento n=0 e Φ=0, si avrà E=0

Considerando che la resistenza di indotto Ri è sempre molto piccola, applicando all'indotto ancora fermo l'intera tensione nominale, la corrente di avviamento Ia assume in genere una intensità così elevata da riuscire pericolosa per la conservazione del motore.

È necessario, allora, provvedere a limitare la corrente di spunto a valori compatibili e questo avviene in due modi:

a)  Avviamento a tensione ridotta

b)  Avviamento a tensione nominale

Avviamento a tensione ridotta

Con questo modo si vuole limitare la corrente di spunto agendo sulla tensione V e allora occorrerà disporre di una sorgente di alimentazione regolabile (che può essere ottenuta con convertitori statici, i quali serviranno anche per la regolazione della velocità).

Così, all'atto dell'avviamento, la tensione applicata sarà molto piccola, appena sufficiente a vincere la caduta ohmica sulla resistenza Ri con la corrente prevista per l'avviamento. All'aumentare dei giri del motore, e quindi della f.c.e.m., la tensione viene via via fatta crescere fino al suo valore nominale.

Avviamento a tensione nominale

Questo tipo di avviamento viene attuato ponendo in serie all'indotto un'opportuna resistenza Ra tramite il cosiddetto reostato d'avviamento.

V

Infatti: Ia = ---- [A]

Ri + Ra

La Ra può essere dimensionata in modo tale che la corrente d'avviamento non superi quella nominale di targa (allora si fa un avviamento a corrente nominale e a coppia nominale perché

C = K'· ·I

Il reostato di avviamento viene inserito nei motori in modo diverso secondo il tipo di eccitazione: derivata, separata o in serie.

1) Motore ad eccitazione in derivata

2)Motore ad eccitazione in serie

In particolare per i motori ad eccitazione derivata (figura 1 ), il reostato di campo Rc deve essere inserito a monte del punto di derivazione del reostato di avviamento Ra; ciò al fine di evitare che all'atto dell'avviamento venga ridotta la tensione ai capi del circuito di eccitazione, col risultato di rendere l'avviamento impossibile per insufficienza di flusso e quindi anche di coppia.

Nel caso invece dell'eccitazione in serie (figura 2), il reostato di avviamento può essere inserito indifferentemente a monte o a valle del motore purché in serie sul circuito di indotto.

Supponendo di impiegare un reostato a gradini; inizialmente, prima di chiudere l'interruttore T, bisogna che il reostato sia tutto inserito e di valore tale che la corrente circolante nel reostato e nell'indotto, in serie fra loro, risulti dello stesso ordine di grandezza della corrente normale In del motore.

Non appena il motore si avvia, si genera nell'indotto la f.c.e.m. E la quale, opponendosi alla corrente, la fa diminuire: man mano che il motore accelera si deve quindi escludere per gradi il reostato di avviamento fino a raggiungere l'esclusione completa ad avviamento ultimato.

Il primo metodo è generalmente impiegato nelle attuali applicazioni dei motori a corrente continua perché non fa uso dei reostati di avviamento.

Il secondo metodo, invece, si applica per i motori industriali e per la trazione elettrica, di non recente installazione.

Regolazione della velocità dei motori a corrente continua

Il problema della regolazione di velocità ha trovato in passato soluzioni diverse a seconda delle potenze in gioco: per le piccole potenze sono state adottate talvolta delle regolazioni reostatiche, che diventano ovviamente inaccettabili per potenze maggiori a causa delle eccessive dissipazioni di energia; per le applicazioni a grandi potenze sono stati invece impiegati i classici gruppi rotanti costituiti da un motore a corrente alternata alimentato da una dinamo ad eccitazione dipendente (come nei gruppi Ward-Leonard).

Più modernamente, invece, il problema della generazione di una tensione continua di ampiezza variabile, necessaria per la variazione di velocità, è stato risolto, per potenze anche ingentissime, grazie ai progressi conseguiti nella tecnica di costruzione e di impiego dei diodi, dei tiristori e transistori di potenza, che costituiscono gli elementi base per la realizzazione dei convertitori statici da corrente alternata, monofase o trifase, alla continua (e viceversa).

Equazioni del motore a corrente continua a eccitazione separata

In base alla teoria dei motori a corrente continua, la velocità di rotazione di un motore a corrente continua è espressa, dalla relazione che qui si riporta in forma semplificata:

E V - Ri ∙ I V

n = --- = ----- ≈ ---

K ∙ Φ K ∙ Φ K ∙ Φ

Questa espressione dimostra che, a parte le cadute ohmiche di indotto Ri ∙ I (che sono in effetti trascurabili rispetto a V), la velocità di rotazione del motore è direttamente proporzionale alla tensione di alimentatore indotto, e inversamente proporzionale invece al flusso per polo Φ che è a sua volta una funzione crescente della corrente di eccitazione Ie .

Nella maggior parte dei casi si attua un tipo di funzionamento per il quale la variazione della velocità viene effettuata modificando unicamente la tensione di alimentazione V, mantenendo invariata invece la corrente di eccitazione Ie, e quindi il flusso Φ: ciò al fine preciso di poter utilizzare a tutte le velocità la coppia motrice nominale del motore, ottenibile imprimendo nel circuito di armatura la corrente nominale In ; tale coppia è espressa dalla seguente relazione:

Cn = K· In · Φ = costante

Si può quindi affermare che, volendo attuare un funzionamento a coppia "disponibile" costante, si deve agire unicamente sulla variazione della tensione di alimentazione di indotto, mantenendo invece costante l'eccitazione.

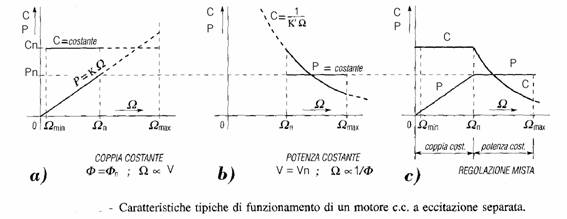
Nell'azionamento a coppia costante la potenza "disponibile", espressa in funzione delle grandezze meccaniche ed elettriche, cresce invece linearmente con la velocità di rotazione e con la tensione V d'armatura, in base alla relazione:

P = · C = V · In

fino al raggiungimento del valore nominale Pn corrispondente alla tensione nominale Vn .

Quando la variazione di velocità viene ottenuta mantenendo costante la tensione di armatura al valore V = Vn e variando invece il flusso di eccitazione, si realizza la regolazione a potenza "disponibile" costante. La relazione mostra infatti che, diminuendo il flusso nominale, la velocità aumenta, mentre la coppia C = Vn · In / ω varia in proporzione inversa alla velocità stessa; la potenza disponibile rimane pertanto costante a tutte le velocità ed è pari a quella nominale (naturalmente il carico può richiedere anche una potenza minore, sicché il motore assorbirà una corrente inferiore alla nominale).

In molte applicazioni si avvia la macchina col massimo flusso di eccitazione e tensione gradualmente crescente fino al valore nominale: la coppia disponibile risulta allora costante, mentre la potenza cresce linearmente con la velocità; raggiunta la velocità nominale, la tensione di armatura non viene più modificata, ma si diminuisce il flusso di eccitazione; in tal modo la velocità aumenta e il motore lavora a potenza disponibile costante, potendo fornire una coppia che diminuisce all'aumentare della velocità ( il carico all'albero deve anch'esso diminuire conseguentemente). Si ottiene così la regolazione mista, illustrata.

Sempre nel caso del motore a eccitazione separata, che presenta il maggior numero di applicazioni nel campo dei controlli automatici, la coppia può esprimersi con la relazione qui riscritta nella forma:

K K²

C = --- V - ---

Ri  Ri

Esaminando quest'espressione si può concludere che esistono le seguenti possibilità di variazione della velocità del motore:

1) (regolazione d'armatura) mantenendo costante il flusso Φ di eccitazione e aumentando la tensione d'armatura V si ha una traslazione verso destra della caratteristica meccanica coppia-velocità: in tal modo, nel funzionamento a coppia utile Cu costante, la velocità si sposta sui valori corrispondenti ai punti 1, 2, 3;

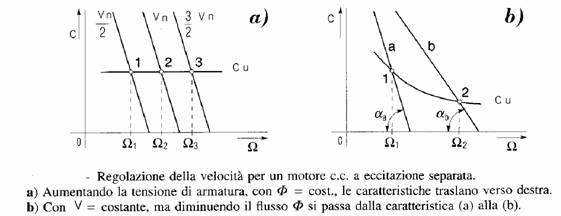
2) (regolazione di campo) mantenendo costante la tensione di alimentazione V e diminuendo il flusso di eccitazione Φ si passa dalla curva (a) alla curva (b), con variazione della pendenza α, e conseguentemente alla velocità da data la caratteristica di carico Cu.

Gruppi Ward-Leonard

Permettono di ottenere un maggior campo di variabilità della velocità e di rendere più agevoli sia le operazioni di avviamento che di frenatura dei motori.

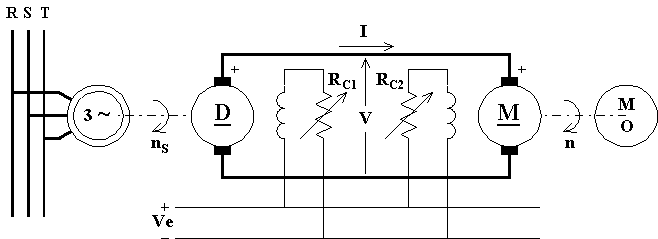
In questo caso si ha la possibilità di regolare il motore (ad eccitazione indipendente) sia attraverso la variazione del reostato di campo R_C2 che della tensione V applicata all'armatura.

La macchina asincrona funziona normalmente da motore e trascina la macchina in corrente continua ad essa coassiale, funzionante da generatore, ad una velocità n_S praticamente costante al variare del carico (considerando i valori contenuti dello scorrimento).

Il motore viene fatto partire con una tensione sufficientemente bassa intervenendo sul reostato di campo R_C1, in tal modo non è necessario il reostato d'avviamento del motore e le perdite in fase di avviamento sono ridotte. Per bassi valori di velocità si fa funzionare il motore con corrente assorbita costante e reostato R_C2 del tutto disinserito, quindi si ha il flusso nel motore praticamente costante (trascurando i fenomeni di saturazione). La velocità viene variata agendo su R_C1 e, quindi, sulla tensione V. In tal modo la coppia del motore è costante (nei limiti in cui sono costanti la corrente assorbita ed il flusso), e la potenza resa dal motore è proporzionale alla velocità n ed, a meno della c.d.t. sulla resistenza interna del motore, alla tensione V. Raggiunta la velocità corrispondente alla tensione massima possibile, si mantiene costante tale tensione massima e si agisce su R_C2 per aumentare la velocità del motore; infatti un aumento del reostato comporta una diminuzione della corrente d'eccitazione e del flusso e quindi un aumento della velocità.

Per invertire il senso di marcia del motore si inverte la polarità dell'eccitazione della dinamo, infatti così facendo viene invertita la polarità della tensione applicata all'armatura del motore.

E' possibile la frenatura a recupero, basta ridurre bruscamente la corrente d'eccitazione della dinamo, in modo che la sua f.e.m. risulti inferiore alla f.e.m. del motore che, ora, funzionerà da generatore erogando una potenza elettrica pari alla propria energia cinetica specifica ed alla potenza meccanica ricevuta dalla macchina operatrice MO. La macchina in corrente continua coassiale con la macchina asincrona funzionerà da motore erogando all'albero la potenza ricevuta sotto forma elettrica e la macchina asincrona funzionerà da generatore riversando in rete l'equivalente potenza elettrica.

Fuga del motore a corrente continua

Nei motori ad eccitazione indipendente o derivata, se viene a mancare, durante il normale funzionamento, la corrente d'eccitazione accade che il flusso si riduce al piccolo valore residuo Φr.

Come conseguenza si ha:

a) la riduzione della f.e.m. al piccolo valore Er = K·Φr·n con il conseguente grande aumento della corrente d'indotto al valore:

Sicuramente la corrente è tale da distruggere il collettore a lamelle nel caso in cui non intervenga una protezione di massima corrente.

b) la coppia del motore diventa C_F = K'·Φr·I_F e può accadere che, nonostante il piccolo valore del flusso, a causa dell'elevatissima corrente tale coppia superi la coppia resistente applicata all'albero determinando un'accelerazione e, quindi, un aumento incontrollabile della velocità del motore (il motore è andato in fuga). Tale meccanismo, una volta innestato, può portare alla distruzione meccanica del motore.

Lo stesso inconveniente può presentarsi anche nel motore con eccitazione composta, tuttavia la presenza dell'eccitazione in serie garantisce la permanenza di un flusso che limita gli inconvenienti dovuti alla cessata eccitazione derivata. Nel caso di motori con eccitazione serie l'inconveniente non può presentarsi perché la mancanza della corrente d'eccitazione significa la contemporanea mancanza della tensione d'armatura (rimane per tali motori il pericolo derivante dal funzionamento a vuoto).