|
|
| |
CIRCUITI ELETTRICI
RL
RC
RLC
CIRCUITO RL
Si dice circuito RL un circuito in cui compaiono solo resistenze e induttanze. Lo schema elettrico è il seguente:
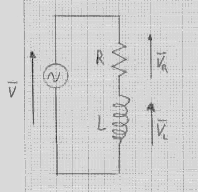
Nel circuito RL si combinano i due effetti della resistenza del resistore R e della reattanza della bobina L, per cui si ha uno sfasamento complessivo tra tensione e corrente, che dipende sia da R che da XL. Si dice impedenza del circuito RL l'ostacolo che esso oppone al passaggio della corrente alternata. L'impedenza si indica con la lettera Z, si misura in si calcola con la seguente formula:
Z = R2 + ( L)2
Z è un vettore il cui modulo lo indichiamo con Z. Tale formula ci dice che il modulo dell'impedenza Z si calcola facendo la radice quadrata della somma di R al quadrato + ( L) tutto al quadrato, che poi è la reattanza al quadrato. Invece Z vettore è : Z = R + j L. La legge di Ohm diventa:
V = Z I = (R + j L) I
Cioè la tensione vettore ai capi di un circuito RL è uguale al prodotto della impedenza Z vettore per la corrente vettore.
Per disegnare i vettori usiamo il seguente schema:
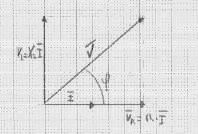
cioè prima disegniamo la tensione ai capi di R che è orizzontale e quindi VR = RI; poi disegniamo la tensione ai capi della induttanza L, che è sfasata di 90° in anticipo quindi VL = j XL I, poi facciamo la somma vettoriale dei due vettori e otteniamo il vettore V, che è la tensione applicata al circuito RL. Per calcolare lo sfasamento cioè l'angolo tra tensione V e corrente I si può usare la seguente formula:
= arctg L/R
cioè arcotangente del rapporto tra parte immaginaria e parte reale.
CIRCUITO RC
Si dice circuito RC un circuito in cui compaiono solo resistenze e condensatori. Lo schema elettrico è il seguente:
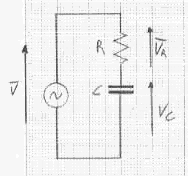
Nel circuito RC si combinano i due effetti della resistenza del resistore R e della reattanza del condensatore C, per cui si ha uno sfasamento complessivo tra tensione e corrente, che dipende sia da R che da XC. Si dice impedenza del circuito RC l'ostacolo che esso oppone al passaggio della corrente alternata. L'impedenza si indica con la lettera Z, si misura in si calcola con la seguente formula:
Z = R2 + (1/ C)2
Z è un vettore il cui modulo lo indichiamo con Z. Tale formula ci dice che il modulo dell'impedenza Z si calcola facendo la radice quadrata della somma di R al quadrato + (1/ C) tutto al quadrato, che poi è la reattanza al quadrato. Invece Z vettore è : Z = R - j (1/C). La legge di Ohm diventa:
V = Z I = (R - j (1/ C) I
Cioè la tensione vettore ai capi di un circuito RC è uguale al prodotto della impedenza Z vettore per la corrente vettore.
Per disegnare i vettori usiamo il seguente schema:
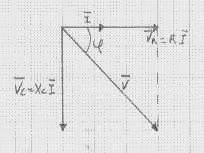
cioè prima disegniamo la tensione ai capi di R che è orizzontale e quindi VR = RI; poi disegniamo la tensione ai capi del condensatore C, che è sfasata di 90° in ritardo VC = - j XC I, poi facciamo la somma vettoriale dei due vettori e otteniamo il vettore V, che è la tensione applicata al circuito RC. Per calcolare lo sfasamento cioè l'angolo tra tensione V e corrente I si può usare la seguente formula:
= arctg - 1 / RC
cioè arcotangente del rapporto tra parte immaginaria e parte reale.
CIRCUITO RLC
Si dice circuito RLC un circuito in cui compaiono resistenze, induttanze e condensatori. Lo schema elettrico è il seguente:
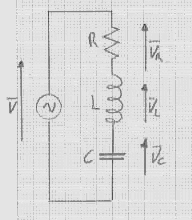
Nel circuito RLC si combinano gli effetti della resistenza del resistore R, della reattanza della bobina L e della reattanza del condensatore C, per cui si ha uno sfasamento complessivo tra tensione e corrente, che dipende sia da R sia da XL sia da XC. Si dice impedenza del circuito RLC l'ostacolo che esso oppone al passaggio della corrente alternata. L'impedenza si indica con la lettera Z, si misura in si calcola con la seguente formula:
Z = R2 + ( L - 1/ C)2
Z è un vettore il cui modulo lo indichiamo con Z. Tale formula ci dice che il modulo dell'impedenza Z si calcola facendo la radice quadrata della somma di R al quadrato + ( L - 1/ C) tutto al quadrato, che poi è la reattanza al quadrato. Invece Z vettore è : Z = R + j ( L - 1/C). La legge di Ohm diventa:
V = Z I = (R + j ( L - 1/ C) I
Cioè la tensione vettore ai capi di un circuito RLC è uguale al prodotto della impedenza Z vettore per la corrente vettore.
Per disegnare i vettori usiamo il seguente schema:
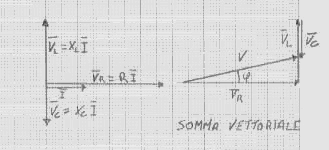
cioè prima disegniamo la tensione ai capi di R che è orizzontale e quindi VR = RI; poi disegniamo la tensione ai capi della induttanza L, che è sfasata di 90° in anticipo quindi VL = j XL I; poi disegniamo la tensione ai capi del condensatore C, che è sfasata di 90° in ritardo VC = - j XC I, poi facciamo la somma vettoriale dei tre vettori e otteniamo il vettore V, che è la tensione applicata al circuito RLC. Per calcolare lo sfasamento cioè l'angolo tra tensione V e corrente I si può usare la seguente formula:
= arctg ( L - 1/ C) / R
cioè arcotangente del rapporto tra parte immaginaria e parte reale.
Esercizi di fisica con soluzioni/Correnti alternate/Circuito RL in corrente alternata
Consideriamo un generatore di corrente alternata come in
figura che funziona a ![]() ,
,
![]() con
in serie una resistenza
con
in serie una resistenza ![]() ,
,
![]() .
Determinare la corrente
.
Determinare la corrente ![]() ,
la tensione efficace ai capi della resistenza
,
la tensione efficace ai capi della resistenza ![]() e
dell'induttanza
e
dell'induttanza ![]() e lo
sfasamento tra corrente
e lo
sfasamento tra corrente ![]() e
generatore, tra
e
generatore, tra ![]() e
generatore, tra
e
generatore, tra ![]() e
generatore.
e
generatore.
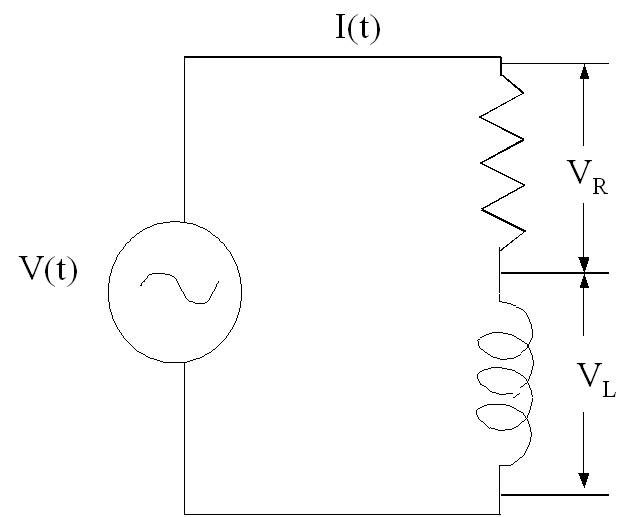
Soluzione:
L'equazione della maglia è (eliminando la variabile tempo esplicitamente dall'equazione):
![]()
![]()
Quindi:
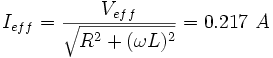
Per quanto riguarda lo sfasamento tra corrente e generatore:
![]()
quindi dall'algebra dei numeri complessi:
![]()
Quindi:
![]()
![]()
Lo sfasamento con il generatore è lo stesso della corrente,
essendo ![]() un
numero reale. Mentre:
un
numero reale. Mentre:
![]()
![]()
Quindi lo sfasamento tra tensione ai capi dell'induttanza e del generatore vale:
![]()
Se la frequenza aumentasse la parte della impedenza dovuta alla induttanza in
serie aumenterebbe al limite rendendo trascurabile la resistenza: il circuito
diventerebbe molto simile ad un semplice condensatore, la tensione ai capi
della resistenza sarebbe trascurabile: un circuito di questo genere, si usa per
eliminare le alte frequenze e si chiama infatti circuito taglia alto.
Esercizi di fisica con soluzioni/Correnti alternate/Circuito RC in corrente alternata
Consideriamo un generatore di corrente alternata come in
figura che funziona a ![]() ,
,
![]() con
in serie una resistenza
con
in serie una resistenza ![]() ,
,
![]() .
Determinare la corrente
.
Determinare la corrente ![]() ,
la tensione efficace ai capi della resistenza
,
la tensione efficace ai capi della resistenza ![]() e del
condensatore
e del
condensatore ![]() e lo
sfasamento tra corrente
e lo
sfasamento tra corrente ![]() e
generatore, tra
e
generatore, tra ![]() e
generatore, tra
e
generatore, tra ![]() e
generatore.
e
generatore.

Soluzione:
L'equazione della maglia è (eliminando la variabile tempo esplicitamente dall'equazione):
![]()
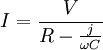
Quindi:
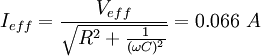
Per quanto riguarda lo sfasamento tra corrente e generatore:
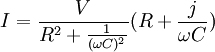
quindi dall'algebra dei numeri complessi:
![]()
Quindi:
![]()
![]()
Lo sfasamento con il generatore è lo stesso della corrente,
essendo ![]() un
numero reale. Mentre:
un
numero reale. Mentre:
![]()
![]()
In questo caso:
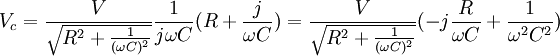
Quindi lo sfasamento tra tensione ai capi del condensatore e generatore vale:
![]()
Se la frequenza diminuisse la parte della impedenza dovuta alla capacità in serie aumenterebbe al limite rendendo trascurabile la resistenza: il circuito diventerebbe molto simile ad un semplice condensatore, la tensione ai capi della resistenza sarebbe trascurabile: un circuito di questo genere, si usa per elimare le basse frequenze e si chiama infatti taglia basso. Notiamo come la pulsazione che delimita il passaggio tra la bassa e l'alta frequenza è quella per cui in modulo le due impedenze in modulo si equivalgono:
![]() cioè:
cioè:
![]()
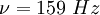 Quindi
a
Quindi
a ![]() la
frequenza è bassa.
la
frequenza è bassa.
Esercizi di fisica con soluzioni/Correnti alternate/Circuito RCL in corrente alternata
Un circuito RCL serie è alimentato alla frequenza di
risonanza. Nella induttanza può al massimo scorrere una corrente ![]() . In
tale condizione estrema determinare:
. In
tale condizione estrema determinare:
a) La differenza di potenziale massima ai capi dei vari elementi circuitali.
b) L'energia fornita in un periodo dal generatore.
c) La frequenza per cui la differenza di potenziale ai capi dell'induttanza sia due volte quella ai capi della capacità.
(dati del problema ![]() ,
, ![]() ,
,
![]() ,
, ![]() )
)
Soluzione:
a) La corrente che scorre alla risonanza, per cui il generatore fornisce una
![]()
ai capi della resistenza vi sono quindi ![]() mentre
detta:
mentre
detta:
![]()
La tensione ai capi del condensatore vale:
e ovviamente la stessa ai capi dell'induttanza:
![]()
b)
La potenza media vale:
![]()
quindi in un periodo:
![]()
da cui:
![]()
c)
Basta imporre che:
![]()
![]()
![]()
Esercizi di fisica con soluzioni/Correnti alternate/Circuito RCRL in corrente alternata
Un circuito costituito da una resistenza ![]() in
parallelo con un condensatore
in
parallelo con un condensatore ![]() , in
serie con un resistenza
, in
serie con un resistenza ![]() ed una
induttanza
ed una
induttanza ![]() .
.
a) Determinare percentualmente quanto la frequenza di risonanza esatta si discosti da quella approssimata.
b) L'impedenza del circuito alla frequenza di risonanza.
c) Il fattore di merito del circuito.
(dati del problema ![]() ,
,
![]() ,
,
![]() ,
,
![]() )
)
a)
L'impedenza totale del circuito vale:
![]()
la parte immaginaria vale:
![]()
che si annulla per:
![]()
mentre la pulsazione approssimata di risonanza vale:
![]()
quindi:
![]()
b)
![]()
c)
![]()
Circuito elettrico In generale, percorso per una corrente elettrica. Il termine è comunemente usato per indicare un percorso chiuso composto da vari dispositivi elettrici, da elementi di collegamento che permettano il passaggio della corrente elettrica, e da un generatore in grado di provocare il flusso di cariche. Un simile circuito è detto "chiuso", mentre un circuito che presenta un'interruzione nel cammino delle cariche è detto "aperto". Viene infine detto "cortocircuito" un circuito chiuso nel quale il percorso fra i terminali del generatore ha impedenza trascurabile, cioè idealmente nulla.
La legge di Ohm
Il flusso delle correnti in un circuito obbedisce ad alcune leggi fisiche, tra le quali è fondamentale la legge di Ohm, così chiamata dal nome del fisico tedesco Georg Ohm. Essa afferma che l'intensità della corrente che si stabilisce in un circuito realizzato con componenti puramente resistivi è direttamente proporzionale alla tensione fornita dal generatore e inversamente proporzionale alla resistenza complessiva del circuito stesso. In termini algebrici, la legge di Ohm può essere espressa nella forma I = V/R, dove I indica l'intensità di corrente, misurata in ampere, V la tensione ai capi del generatore, in volt, e R la resistenza del circuito, in ohm (Vedi Unità di misura elettriche). La legge di Ohm è valida per qualsiasi circuito elettrico (o anche componente) puramente resistivo, sia nel funzionamento con corrente continua (DC, dall'inglese direct current), sia in quello con corrente alternata (AC, dall'inglese alternated current); tuttavia per analizzare circuiti complessi o circuiti in AC contenenti induttori (vedi Induzione) e/o condensatori è necessario applicare anche altre leggi fisiche.
Un circuito in cui ciascun collegamento è realizzato in modo che tutta la corrente passi da un componente al successivo senza mai distribuirsi o diramarsi è detto circuito "serie"; esso si presenta come un unico anello senza diramazioni.
Se due o più resistori sono collegati in serie, la resistenza totale è pari alla somma delle singole resistenze. Due resistori si dicono invece "in parallelo" se sono sottoposti alla stessa differenza di potenziale, cioè se i due terminali di ciascun elemento sono collegati a una coppia comune di punti; in questo caso, la resistenza complessiva è data dalla formula
![]()
È evidente che la resistenza complessiva (o equivalente) di più resistori in parallelo è sempre minore della più piccola delle singole resistenze coinvolte; nel caso di due resistenze uguali, ad esempio, la resistenza equivalente del parallelo è esattamente la metà di ciascun valore singolo. Nel collegamento in parallelo, tutti i dispositivi coinvolti sono sottoposti alla stessa differenza di potenziale; in altre parole, il terminale a polarità positiva (+) di ciascuno di essi sarà collegato a un conduttore comune, e analogamente i terminali a polarità negativa (-) saranno collegati a un altro conduttore comune. Nei circuiti in alternata o con correnti comunque variabili, devono essere considerati anche componenti diversi dai resistori.
Le leggi di Kirchhoff
Quando un circuito contiene diramazioni, le correnti e le tensioni si distribuiscono tra i vari componenti secondo due leggi scoperte dal fisico tedesco Gustav Robert Kirchhoff, e conosciute pertanto come leggi di Kirchhoff; a esse si deve fare riferimento nell'analisi di questi circuiti. La prima legge di Kirchhoff afferma che, dato un nodo, cioè un punto di giunzione tra i terminali di due o più componenti, la somma delle correnti che si dirigono verso di esso è, in ogni istante, uguale alla somma di quelle che da esso si allontanano. La seconda legge afferma che, se si passa da un nodo all'altro nella rete fino a compiere un qualsiasi cammino chiuso, cioè una maglia, e si considerano solo i bipoli che compongono questo percorso, la somma algebrica delle forze elettromotrici presenti in essi è pari alla somma algebrica dei prodotti di ciascuna resistenza per la corrente che la percorre.
L'impedenza
L'applicazione della legge di Ohm ai circuiti percorsi da correnti alternate è complicata dalla presenza di effetti capacitivi e induttivi. L'induttanza ritarda i picchi delle correnti alternate rispetto ai picchi delle relative tensioni, mentre la capacità ritarda i picchi delle tensioni rispetto a quelli delle relative correnti. Entrambi gli effetti limitano l'intensità delle correnti in regime alternato e devono essere tenuti presenti nella risoluzione di circuiti percorsi da tali correnti. L'intensità della corrente alternata che fluisce in un circuito AC può essere determinata graficamente per mezzo di rappresentazioni vettoriali, oppure tramite l'equazione algebrica
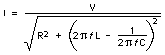
in cui L rappresenta l'induttanza, C la capacità ed f la frequenza della corrente considerata. La grandezza a denominatore nella frazione è detta "impedenza" del bipolo o del tratto di circuito in esame (a una data frequenza) ed è, di solito, rappresentata con la lettera Z; la legge di Ohm per i bipoli e i circuiti a corrente alternata può quindi essere espressa con la semplice equazione I = V/Z. Vedi anche Elettricità.
Elettricità
Esistono due stati opposti di elettricità, convenzionalmente definiti negativo e positivo.
È possibile che due corpi vengano elettrizzati.
Gli stati elettrici si originano perché gli atomi sono formati da elettroni, caricati negativamente, e da protoni caricati positivamente.
La corrente elettrica si gehera quando si ha uno spostamento ordinato di elettroni.
La corrente elettrica viene mantenuta cia una differenza di potenziale.
L0 STATO ELETTRICO DEI CORPI
A tutti è capitato di camminare su un tappeto (o su una moquette) e di sentire una scossa elettrica toccando la maniglia della porta, o di notare pettinandosi in una giornata particolarmente secca, di sentire i capelli scricchiolare e di vedere il pettine (purché non metallico) attirare i capelli che viceversa tendono ad allontanarsi tra loro. Se infine si strofina con un panno di lana una penna o un righello di plastica, entrambi diventano capaci di attirare piccoli pezzetti di carta.
In tutti questi casi ci troviamo davanti a un particolare tipo di fenomeno: un fenomeno elettrico.
Per poter studiare meglio la faccenda,
proponiamo una semplice esperienza: utilizzando due bacchette di plastica e una
di vetro; strofinando entrambe le bacchette di plastica con un panno di lana e
appendone una a un supporto per mezzo di un filo in modo da costruire un
piccolo pendolo.
Quando si avvicina al pendolo l'altra
bacchetta di plastica si osserva che le due bacchette tendono ad allontanarsi.
Si verifica cioè una repulsione.
Strofinando la bacchetta di vetro con
la lana e avvicinandola al pendolo di plastica; questa volta si osserverà che
le bacchette tendono ad avvicinarsi.
Si è verificata cioè un'attrazione. Da questa semplice esperienza si possono trarre alcune importanti conclusioni:
le varie sostanze, per effetto dello strofinio, acquistano una proprietà che prima non avevano: lo stato elettrico;
gli stati elettrici che la materia può assumere sono di due tipi: per convenzione i fisici hanno stabilito di chiamare positivo (+) lo stato elettrico acquistato dal vetro e negativo (-) quello acquistato dalla plastica. Più comunemente si dice che il vetro si è caricato positivamente e la plastica negativamente;
corpi carichi dello stesso segno si respingono e corpi carichi di segno opposto si attraggono.
Ma lo stato elettrico acquistato da un corpo può passare a un altro? E che ne è del panno con il quale si è rispettivamente strofinato la plastica e il vetro?
Prima di rispondere procediamo a un secondo esperimento: si prenda una pallina abbastanza leggera (di sughero o di plastica), si ricopra di carta stagnola e si appenda a mo' di pendolino; con la bacchetta di plastica ancora carica si tocchi la pallina: si noterà che, subito dopo il contatto, la pallina viene respinta.
Questo si spiega pensando che lo stato elettrico negativo
della plastica è passato alla pallina e quindi, essendo dello stesso segno, i
due corpi si respingono.
Se adesso si avvicina alla pallina il panno di lana che è servito a «caricare»
la plastica si osserverà che essi si attirano: questo significa che la pallina,
e quindi la plastica, sono cariche, o hanno una carica, di segno opposto alla
lana.
Da questa seconda esperienza si
possono trarre allora altre importanti conclusioni:
l'elettricità può essere trasferita per contatto;
strofinando tra loro due corpi di materiali diversi essi si caricano di segno opposto.
Quando si manifesta uno stato elettrico, contemporaneamente si manifesta quello di segno opposto.
Attenzione, però! Prima di essere strofinati, gli oggetti dei nostri esperimenti non dimostravano di possedere né elettricità positiva, né elettricità negativa; erano, come si dice, elettricamente neutri.
Allora quale è stata la causa che ha fatto acquistare ad essi elettricità abbandonando lo stato neutro?
L'ipotesi più probabile è che ogni corpo abbia in sé
cariche positive e negative in numero uguale, tali quindi da compensarsi a
vicenda: per questa ragione un corpo, normalmente, non presenta alcuno stato
elettrico.
Lo strofinio sarebbe il sistema con il quale si aggiungono o si tolgono al
corpo cariche di un dato segno, alterando l'equilibrio elettrico naturale e facendo
prevalere in esso uno dei due stati elettrici, il positivo o il negativo.
L'ELETTRICITÀ E IL MODELLO ATOMICO
Per comprendere la natura dei fenomeni elettrici occorre
riprendere il discorso sulla struttura dell'atomo. L'atomo è costituito da
cariche elettriche di segno opposto e in uguale quantità in modo che
complessivamente abbia carica elettrica nulla, cioè sia neutro.
E stato sperimentalmente dimostrato che ogni atomo è costituito da un nucleo
centrale e da un certo numero di elettroni rotanti attorno ad esso. Il nucleo è
formato da protoni e neutroni, tenuti assieme da forze di grande intensità ma
aventi un brevissimo raggio d'azione. I protoni hanno carica elettrica
positiva, i neutroni non hanno carica elettrica; la carica degli elettroni è
uguale a quella dei protoni, ma ha segno opposto, è cioè negativa.
Se sull'atomo non agisce alcuna causa esterna, gli elettroni continuano a
ruotare intorno al nucleo senza dar luogo ad alcun fenomeno particolare. In
tale condizione si dice appunto che l'atomo è elettricamente neutro. Se con
mezzi adatti si sottraggono agli atomi di un corpo uno o più elettroni, diciamo
che il corpo si è elettrizzato positivamente, perché avendo perduto elettroni
prevale in esso la carica positiva dei protoni del nucleo; mentre se si
aggiungono agli atomi di un corpo uno o più elettroni, diciamo che si è
elettrizzato negativamente, perché ha acquistato un numero maggiore di
elettroni.
Il mezzo più semplice per aggiungere o per sottrarre elettroni all'atomo di un corpo è appunto lo strofinio.
L'elettricità è pertanto un fenomeno che dipende dallo stato delle particelle elettricamente cariche, che costituiscono gli atomi.
Ad esempio, strofinando fa plastica con la lana, alcuni elettroni sono passati alla plastica che si è così caricata negativamente, mentre la lana si è caricata positivamente (avendo ora un eccesso di protoni).
Ma le cose possono anche andare diversamente: l'elettrizzazione cioè può avvenire anche senza passaggio di elettroni da un corpo all'altro.
Se un palloncino di gomma elettrizzato negativamente viene posto vicino a un altro palloncino non elettrizzato, le sue cariche negative respingono gli elettroni del secondo palloncino, facendoli allontanare. In tal modo, il secondo palloncino, pur rimanendo nel suo complesso elettricamente neutro, presenta una prevalenza di cariche positive nella regione più vicina al palloncino elettrizzato, di cariche negative nella parte più lontana. Sui due palloncini vengono così a fronteggiarsi cariche di segno opposto; di conseguenza i palloncini si attraggono. Questo tipo di elettrizzazione a distanza tra un corpo carico e uno neutro, che è sempre causa di attrazione mai di repulsione, viene detta elettrizzazione per induzione.
ELETTRICITÀ IN MOVIMENTO
Torniamo un istante all'esperienza descritta un partenza: una volta che sia elettrizzata la pallina ricoperta di carta stagnola, si provi a toccarla con le mani; avvicinando poi ad essa la bacchetta di plastica si osserverà che la pallina resta immobile mostrando di aver perduto la sua carica.
Questo non accade invece né al vetro né alla plastica: vetro e plastica conservano a lungo il loro stato elettrico. Tutti i materiali (in particolare i metalli e lo stesso corpo umano), che si comportano come la pallina coperta di stagnola si dicono conduttori; si chiamano invece isolanti quelli che si comportano come il vetro e la plastica.
Gli elettroni che ricoprivano la superficie della pallina passano attraverso il corpo e si disperdono a terra, proprio per la loro capacità di muoversi liberamente sia attraverso la pallina sia attraverso il corpo umano.
Ciò non avviene invece per la plastica e il vetro: solo le cariche a diretto contatto con le dita possono passare attraverso il corpo e disperdersi a terra, le altre restano «intrappolate» e impossibilitate a muoversi.
Tutte le volte che abbiamo a che fare con elettricità in movimento parleremo di corrente elettrica e poiché essa può stabilirsi, con vari meccanismi, attraverso la materia in tutti i suoi diversi stati di aggregazione, e cioè nei solidi, nei liquidi e nei gas, è utile chiarire che cosa causa il movimento delle cariche elettriche, cioè che cos'è la differenza di potenziale.
Si dice che un conduttore, preventivamente caricato, si trova a un certo potenziale quando le cariche elettriche depositate su di esso lo possono abbandonare non appena il corpo venga collegato al suolo ("a terra") tramite un altro conduttore: tanto più il corpo è carico tanto più è elevato il suo potenziale.
Analogamente si dice che tra due corpi esiste una differenza di potenziale quando ciascuno di essi si trova a potenziale diverso.
La differenza di potenziale elettrico può essere paragonata alla differenza di livello di un liquido contenuto in recipienti diversi.
Se i due corpi vengono posti a contatto per mezzo di un conduttore, si stabilirà tra di essi una corrente che si estinguerà non appena la carica sia divenuta uguale su ciascun corpo.
Esistono dei corpi conduttori capaci di mantenere ai loro estremi una differenza di potenziale anche quando tali estremi sono collegati da un conduttore: questi corpi vengono detti generatori.
Supponiamo di stabilire una differenza di potenziale tra due lastre, o meglio tra due elettrodi di metallo, e di interporre tra essi un conduttore (i conduttori hanno la caratteristica che quasi tutti i loro atomi hanno almeno un elettrone molto poco «legato» al nucleo e quindi praticamente libero di muoversi verso l'elettrodo positivo. Si avrà così un passaggio di corrente.
Se tra gli elettrodi si interpone invece un isolante, come il vetro, la porcellana ecc., non vi sarà passaggio di corrente ma un fenomeno, chiamato polarizzazione: gli atomi si «tendono» come elastici ma gli elettroni non riescono ad abbandonare il nucleo.
Anche un liquido può condurre la corrente. Per provarlo immergiamo gli elettrodi in una bacinella contenente acqua salata. Ricordiamo che le molecole di sale sono composte da un atomo di sodio che ha perso un elettrone (ione positivo) e da uno di cloro, che invece ha un elettrone in più (ione negativo).
Quando il sale entra in soluzione nell'acqua, gli ioni di sodio e di cloro si separano e, poiché sono carichi, migrano verso gli elettrodi di segno opposto al loro, determinando passaggio di corrente elettrica.
LA PILA E IL CIRCUITO ELETTRICO
Fino quasi alla fine del 1700 l'unica forma di elettricità che si sapeva ottenere era l'elettricità statica, cioè quella che veniva generata per strofinio. Non si era in grado cioè di produrre correnti elettriche durevoli.
Fu Luigi Galvani (1737-1798), professore di anatomia all'università di Bologna, ad osservare per primo, durante i suoi studi sulla propagazione degli impulsi nervosi, che quando si toccavano i nervi scoperti di una rana con due metalli diversi - rame e argento oppure zinco e rame - si produceva una piccola scarica che faceva contrarre i muscoli dell'animale.
Quest'effetto (detto elettricità animale) venne subito messo in relazione con i diversi metalli impiegati e sfruttato da Alessandro Volta per realizzare uno strumento di grande utilità per gli studi successivi, la pila, per mezzo della quale era possibile produrre una scarica di notevole durata.
Nella pila di Volta vi erano un disco di rame e un disco di zinco, separati da un disco di panno imbevuto in una soluzione acquosa di acido solforico: questi tre dischi ne formavano un elemento. La pila era formata da parecchi di questi elementi appoggiati uno sopra l'altro. Alle sue estremità, o poli, vi era da una parte un disco di rame (polo positivo o anodo, +) e dall'altra un disco di zinco (polo negativo o catodo, -).
Il contatto tra i due poli era stabilito mediante due fili
di rame attaccati rispettivamente uno allo zinco all'estremità inferiore della
pila e l'altro al rame all'estremità superiore.
Quando il circuito veniva "chiuso", si aveva il passaggio continuo di
elettricità.
Si determinava cioè la comparsa di una corrente elettrica, che circolava dal
polo positivo al polo negativo per ritornare al polo positivo di partenza, dopo
avere attraversato l'interno della pila.
Mettendo dunque a contatto due metalli diversi si origina elettricità: la pila
di Volta era il primo generatore di corrente.
Le comuni pile sono altrettanti generatori di corrente. Esse sono contrassegnate con i segni «più» e «meno» in corrispondenza di due zone, chiamate poli, nelle quali l'equilibrio elettrico è stato turbato.
Più precisamente, si sono costretti elettroni a spostarsi da un polo all'altro, così che dove risultano in eccesso prevale la carica negativa, dove ne mancano prevale la carica positiva: i poli hanno potenziale elettrico diverso.
Quando si collegano i poli di una pila con un conduttore, si genera in questo un flusso di elettroni, cioè una corrente elettrica
L'insieme costituito dal generatore, cioè dalla pila, e dal filo conduttore collegato ai suoi poli si chiama circuito elettrico.
Come in un circuito idraulico l'energia dell'acqua è sfruttata per mettere in moto le pale di un mulino o di una turbina, così in un circuito elettrico l'energia degli elettroni in movimento è sfruttata dai cosiddetti apparecchi utilizzatori quali: le comuni lampadine da illuminazione, gli apparecchi riscaldatori, alcuni tipi di motori, gli elettrodomestici.
Opportuni dispositivi, detti interruttori, consentono o
meno il passaggio della corrente nel circuito a seconda della necessità di una
sua utilizzazione.
La presenza degli interruttori fa sì che nel circuito si vengano a determinare
due possibili situazioni:
l'interruttore è inserito: i due fili collegano i due poli della pila con le due parti metalliche della lampadina; nel circuito passa la corrente, come viene rivelato dall'accensione della lampadina. In questo caso il circuito si dice chiuso;
l'interruttore è disinserito: il collegamento tra pila e lampadina è interrotto; non passa corrente e la lampadina è spenta. In questo caso il circuito si dice aperto.
EFFETTI DELLA CORRENTE ELETTRICA E SUA MISURA
Abbiamo già osservato il meccanismo di conduzione della corrente nei liquidi a proposito del sale da cucina (NaCl). Ora vogliamo vedere il fenomeno sotto un altro aspetto. Quando lo ione Cl arriva all'elettrodo positivo, cede il suo elettrone in più all'elettrodo stesso, diventando neutro. Così succede per lo ione Na che, una volta arrivato all'elettrodo negativo, riacquista l'elettrone che gli mancava diventando anch'esso neutro.
Cloro e sodio rimangono dunque depositati intorno al rispettivo elettrodo. Qual è il risultato del passaggio di corrente?
E molto semplice: la molecola di sale NaCI è stata scomposta nei suoi due componenti sodio e cloro che possono essere recuperati agli elettrodi.
L'effetto chimico del passaggio di corrente consiste appunto in questo fenomeno, chiamato elettrolisi.
Un altro effetto della corrente elettrica di notevole importanza per le sue numerose e utili applicazioni è l'effetto termico, che consiste nel riscaldamento di un conduttore quando questo viene attraversata dalla corrente.
Infatti gli elettroni in movimento che formano la corrente urtano continuamente gli atomi del conduttore incontrando una resistenza durante il loro moto.
La resistenza elettrica è paragonabile all'attrito che si manifesta nella zona di contatto tra due corpi in moto reciproco: come una parte dell'energia posseduta dai due corpi viene inevitabilmente dissipata in calore per vincere l'attrito, così una parte dell'energia elettrica che percorre un conduttore viene trasformata in calore.
Spesso, è utile inserire una resistenza in un circuito elettrico, proprio per sfruttare l'energia che gli elettroni, ostacolati nel loro fluire, sono costretti a cedere agli atomi in quel tratto di circuito.
La più comune applicazione di questo effetto è la lampadina a incandescenza, nella quale il riscaldamento prodotto nel filamento a causa del passaggio di corrente è tale da portare il filamento stesso all'incandescenza, così che possa emettere luce.
Le applicazioni dell'effetto termico della corrente sono tantissime. Il ferro da stiro, che viene normalmente utilizzato nelle nostre case, si riscalda grazie a delle resistenze che appunto sfruttano tale effetto. Lo stesso principio viene utilizzato dall' asciugacapelli, dal tostapane e dalla stufa elettrica.
L'ultimo effetto della corrente elettrica è quello magnetico: un conduttore percorso da corrente è in grado di influenzare l'ago di una bussola posta nelle sue vicinanze.
Naturalmente è importante poter misurare l'intensità di una
corrente elettrica, cioè il numero di cariche elettriche (quantità di
elettricità) che nell'unità di tempo (in un secondo) passano attraverso la
sezione di un conduttore.
L'unità di misura dell'intensità di corrente è l'ampere (A). Un
ampere è uguale a 6,25 x 1018 elettroni al secondo.
Come si è appreso, in una pila elettrica vi è un accumulo
di elettroni in corrispondenza di uno dei due poli.
Evidentemente per determinare questo accumulo è stato compiuto del lavoro: ne
consegue che gli elettroni hanno acquistato energia potenziale e il polo ove si
trovano è descritto come una zona ad alto potenziale (+).
Viceversa l'altro polo che non ha accumulato elettroni, è descritto come una
zona di basso potenziale (-).
La differenza di potenziale fra i due elettrodi si chiama voltaggio (o tensione). Il voltaggio è una misura dell'energia disponibile per muovere le cariche di un circuito: il voltaggio si misura in volt (V).
E il voltaggio che fa scorrere le cariche in un circuito: più alto è il voltaggio, maggiore è il numero d'elettroni che può scorrere in un conduttore. Il numero di elettroni che può scorrere in un conduttore può essere paragonato alla quantità d'acqua che può scorrere in una tubazione; il voltaggio del conduttore si può paragonare alla pressione dell'acqua nella tubazione.
La quantità d'acqua che può fluire in una tubazione dipende dalla pressione dell'acqua. In simil modo, il numero di elettroni che può fluire in un conduttore dipende dal voltaggio.
Il numero di elettroni che può scorrere in un conduttore dipende anche dalla resistenza. L'unità di misura della resistenza è l'ohm. Parecchi sono i fattori che influenzano la resistenza di un conduttore:
la temperatura: quando la temperatura di un conduttore aumenta, aumenta anche là sua resistenza;
il diametro de/conduttore: quando il diametro del conduttore è maggiore, la sua resistenza diminuisce, proprio come un tubo per l'acqua di ampie dimensioni consente un flusso maggiore d'acqua rispetto a un tubo di diametro più stretto;
la lunghezza: maggiore è la lunghezza del conduttore, maggiore è la sua resistenza. Questa maggiore resistenza può essere paragonata all'acqua che scorre attraverso un lungo tubo. L'acqua scorre con maggiore difficoltà attraverso un tubo lungo che attraverso un tubo corto;
la natura del conduttore: gli elettroni scorrono più facilmente attraverso i materiali conduttori che attraverso gli isolanti.
Non tutti i conduttori trasportano la stessa quantità di corrente elettrica. Per esempio, un filo collegato a una stufa elettrica trasporta maggior quantità di corrente di uno collegato a una lampadina.
L'intensità della corrente e la resistenza sono due grandezze inversamente proporzionali.
Di quanto è maggiore l'una, di tanto l'altra è minore e
viceversa.
La relazione tra voltaggio (tensione), intensità di corrente e resistenza si
esprime con la legge di Ohm secondo la quale: ad una tensione maggiore
corrisponde un'intensità di corrente maggiore; ad una resistenza maggiore
corrisponde una intensità di corrente minore.
Questa legge è molto importante poiché consente di determinare una delle tre
grandezze, quando sono note le altre due.
Se indichiamo con V la tensione, con I l'intensità e con R la resistenza, si ha la formula
I = V / R
Da essa si possono ricavare le altre due formule:
V = I x R
R= V / I
I GENERATORI DI CORRENTE ELETTRICA
I principali generatori di corrente elettrica sono: le pile, gli accumulatori, le dinamo e gli alterrnatori.
Pile e accumulatori sono generatori chimici: producono energia elettrica, a partire da quella chimica, in base a un processo simile a quello dell' elettrolisi.
Le pile sono utilizzate per far funzionare radioline, giradischi, registratori, orologi elettrici, cineprese e, in generale, tutti gli apparecchi portatili, che funzionano indipendentemente dall'allacciamento alla rete elettrica, e che non richiedono tensioni troppo elevate.
Negli accumulatori a piombo alcune lastre di piombo, alternate a lastre di biossido di piombo, sono immerse in acido solforico diluito con acqua distillata.
Nella fase di scarica l'accumulatore eroga energia elettrica ottenuta dalla trasformazione di energia chimica: le lastre di piombo liberano elettroni che sono acquisiti dalle lastre di biossido. In questo processo l'acido solforico si combina con il biossido di piombo dando solfato di piombo; quando tutto l'acido solforico si è trasformato, l'accumulatore smette di funzionare; si deve allora procedere alla sua carica, fornendo energia elettrica alle piastre (il processo chimico allora s'inverte).
Nella pila, due elettrodi di metallo diverso sono immersi in una soluzione elettrolitica; l'anodo è costituito da un metallo che tende a sovraccaricarsi di elettroni mentre il catodo è l'elettrodo che tende a perdere elettroni; lo spostamento di elettroni dal catodo all'anodo genera la corrente elettrica.
Nelle pile in uso si è sostituita la soluzione (corrosiva e difficilmente trasportabile) con una sostanza gelatinosa resa compatta.
Le pile in uso sono costituite da un catodo di carbone, posto al centro dell'impasto gelatinoso, circondato da un involucro di zinco che funziona da anodo; il tutto è rivestito da un involucro isolante e protettivo da cui escono solo le piastrine per il collegamento.
Con il tempo l'anodo di zinco si ossida diventando inutilizzabile: ecco perché le pile sono generatori limitati nel tempo (devono essere sostituite di frequente).
Sono attualmente in commercio anche pile (pile al cadmio-nichel) che funzionano come accumulatori di piccole dimensioni, perché possono essere ricaricate.
POTENZA ELETTRICA
L'energia elettrica si trasforma in altra forma di energia: luminosa (nelle lampadine), termica (nelle stufe), sonora (negli stereo).
Non tutti i dispositivi elettrici usano la medesima quantità di energia. Supponiamo di voler riscaldare una stanza usando l'energia elettrica: allo scopo userai una stufa elettrica che emette una maggiore quantità di calore di un asciugacapelli e che consumerà anche più corrente dell'asciugacapelli funzionando per lo stesso periodo di tempo.
Quanta più corrente usa un apparecchio elettrico, tanto
maggiore è l'energia elettrica che consuma. La quantità di energia elettrica
consumata nell'unità di tempo (secondo) si chiama potenza elettrica.
La potenza della stufa elettrica è maggiore di quella dell'asciugacapelli
poiché la stufa utilizza una quantità maggiore di energia elettrica al secondo
rispetto all' asciugacapelli
La potenza si misura in watt (W). La potenza è il lavoro che si compie in rapporto al tempo che si impiega a compierlo; poiché il lavoro è energia, possiamo considerare la potenza come l'energia trasformata nell'unità di tempo.
Perciò se una lampadina "consuma' energia elettrica in ragione di 60 Joules al secondo, trasforma ad ogni secondo 60 Joules di energia elettrica in energia luminosa e in energia termica: ha quindi una potenza di 60W.
Più alto è il numero di watt, più intensa è la luce emessa
dalla lampadina e maggiore è l'energia che consuma. Un'unità di potenza
superiore al watt è il kilowatt (kW).
Un kilowatt è un'unità di potenza uguale a 1000 watt, ossia 1000 joule al
secondo.
Conduttori e isolanti Una lampadina è collegata con fili di rame in un circuito aperto. Se si chiude il circuito con oggetti diversi si osserva che la lampadina si accende solo nel caso di determinati oggetti. Si può utilizzare l'accensione o meno della lampadina per classificare gli oggetti usati per la chiusura del circuito come conduttori (che permettono l'accensione) o isolanti (che impediscono l'accensione).
La tensione di alimentazione Tre lampadine identiche sono collegate rispettivamente a tre pile da 4,5 V, 3 V e 1,5 V. L'intensità luminosa prodotta dalle tre lampadine è corrispondentemente decrescente.
L'additività delle tensioni di alimentazione Una lampadina viene collegata alla pila da 4,5 V e un'altra identica ad un sistema di tre pile da 1,5 V in serie: si osserva che la luminosità delle lampadine è uguale.
L'alimentazione in parallelo Si collega una pila da 4,5 V a tre lampadine identiche in parallelo. Accanto, un'unica lampadina viene collegata con una pila da 4,5 V. Tutte le lampadine hanno la stessa luminosità. Si può osservare anche che dopo aver svitato una delle lampadine, le altre restano accese.
Lampadine in serie Si alimentano tre lampadine uguali collegate in serie con una pila da 4,5 V. La luminosità delle lampadine è la stessa e appare circa un terzo di quella di un'unica lampadina collegata con una pila da 4,5 V.
Alimentazione in parallelo per lampadine in serie Due lampadine in serie vengono alimentate con una pila da 4,5 V e successivamente con due pile da 4,5 V in parallelo. La luminosità di ciascuna lampadina è in ogni caso uguale a quella di una singola lampadina alimentata con una pila da 4,5 V.
Il reostato Un lungo filo conduttore avvolto su un cartoncino costituisce l'elemento resistivo (reostato) di un circuito costituito da una lampadina e una pila da 4,5 V. Prelevando con un cursore una lunghezza decrescente di tale filo conduttore si osserva l'accensione della lampadina con intensità crescente. Si comprende così il ruolo di una resistenza variabile in un circuito.
Il deviatore Il circuito costituisce il più semplice esempio di deviatore.
Elementi elettrici lineari
Come abbiamo già detto, un circuito si compone di vari elementi. Tra questi vi sono gli elementi cosiddetti lineari, che si definiscono tali in quanto le loro caratteristiche sono costanti, cioè indipendenti dalla tensione o dalla corrente che gli applichiamo.
Gli elementi elettrici lineari si dividono in elementi attivi, cioè in grado di fornire energia, ed elementi passivi.
|
|
Fig.1: Elementi lineari passivi |
|
Fig.2: Elementi lineari attivi |
|
Vediamo allora quali sono le caratteristiche di questi elementi dandone una breve descrizione (più avanti vedremo meglio e in dettaglio i vari componenti):
-Resistenza
Come abbiamo già visto, la resistenza è un parametro che esprime la tendenza ad
opporsi al passaggio di corrente, e la relazione che c'è tra la tensione e la
corrente in una resistenza è espressa dalla formula:
V = R · I (legge di Ohm)
Senza tornare sull'argomento, già trattato nel capitolo 1, ricordiamo semplicemente che la resistenza si misura in ohm, che il suo inverso è la conduttanza, e che, poichè il passaggio di corrente provoca una dissipazione termica per effetto joule, la potenza dissipata è:
|
P = V·I = R·I2 = |
V2 |
-Capacità
Esprime la proprietà di accumulare una certa quantità di cariche su due
conduttori, detti armature, separati da un materiale isolante, detto
dielettrico.
La capacità C è il rapporto tra la carica Q immagazzinata e la tensione V tra
le due armature
|
C = |
Q |
Per il SI l'unità di misura è il coulomb/volt, che corrisponde al farad (F):
1F = 1C/V
La corrente I che fluisce a causa di una variazione della tensione tra le armature è pari a:
|
I = C |
dV |
mentre l'energia W immagazzinata da una capacità C sottoposta ad una tensione V equivale a:
|
W = C |
V2 |
-Induttanza
Detta anche coefficente di autoinduzione, rappresenta la proprietà di un
dispositivo di generare un campo magnetico quando viene percorso da corrente
elettrica.
La tensione ai capi di una induttanza L è proporzionale alla variazione della
corrente I secondo la relazione
|
V = L |
dI |
mentre l'energia W immagazzinata da una induttanza L percorsa da una corrente I è pari a:
|
W = L |
I2 |
L'unità di misura dell'induttanza è l'henry (H).
-Generatore di tensione
Idealmente un generatore di tensione è un elemento attivo che è in grado di
mantenere ai suoi capi una determinata tensione V, indipendentemente dalla
quantità di corrente erogata e in modo costante nel tempo.
Nella realtà però questi dispositivi presentano ovviamente dei limiti, che vedremo
in seguito.
-Generatore di corrente
Un generatore di corrente è un elemento attivo che, idealmente, è in grado di
erogare una determinata corrente I, qualsiasi sia la tensione ai suoi capi,
ovvero qualunque sia il carico collegato ai suoi capi, e in modo costante nel
tempo.
Anche quì, come per il generatore esistono degli ovvi limiti che analizzeremo
in seguito.
Elementi in serie, elementi in parallelo
-Serie
Due o più elementi elettrici si definiscono collegati in serie se sono percorsi
dalla stessa corrente. Quando degli elementi sono posti in serie è possibile
calcolarne il valore totale, che definiamo valore equivalente, secondo le
seguenti regole:
-il valore della resistenza equivalente Req è data da
Req = R1 + R2 + R3 + ... + Rn
-analogamente il valore della induttanza equivalente Leq è data da
Leq = L1 + L2 + L3 + ... + Ln
-in modo diverso si calcola invece la capacità equivalente Ceq poichè
|
|
|
|
|
|
|
1 |
|
1 |
da cui possiamo ricavare che
|
Ceq = |
|
|
|
|
Fig.3: Un elsempio di elementi in serie |
-Parallelo
Due o più elementi si dicono invece collegati in parallelo se ai loro capi è
applicata la stessa tensione. Anche in questo caso è possibile calcolarne il
valore equivalente in base alle seguenti regole:
-per il valore della resistenza si ha
|
|
|
|
|
|
|
|
|
|
=> |
Req = |
|
-e per l'induttanza
|
1 |
|
1 |
|
1 |
|
1 |
|
|
=> |
Leq = |
|
-mentre, come potete immaginare, per la capacità si ha
Ceq = C1 + C2 + C3 +...+ Cn
E' un modo molto comune indicare il parallelo tra due elementi, in modo simbolico, con due slash tra gli elementi considerati. Per esempio:
Req = R1//R2
Leq = L1//L2
Ceq = C1//C2
|
|
|
Fig.4: Un elsempio di elementi in parallelo |
Vari tipi di segnale
Con il termine segnale intendiamo generalmente indicare tensioni o correnti che seguono una certa evoluzione temporale, e che riscontriamo nei circuiti elettrici che esaminiamo. Definiamo poi con il termine forma d'onda l'insieme dei valori istantanei assunti da un segnale.
Esistono vari tipi di segnali, ma comunque tutti
riconducibili a due principali categorie: i segnali periodici e i segnali
aperiodici (o non periodici). Nel primo caso siamo di fronte a un segnale che
si ripete in modo ciclico, ad intervalli di tempo che chiamiamo perido e
indichiamo con T, e che seguono una determinata legge matematica che ne
determina l'andamento.
Il numero di periodi che si ripetono nell'unità di tempo definisce la frequenza
f del segnale, ovvero
|
f = |
1 |
che si misura in hertz (Hz).
Per descrivere le caratteristiche dei segnali periodici si
ricorre alla definizione di alcuni parametri. La frequenza appena citata è uno
di questi, ma vi sono anche per esempio l'ampiezza massima dell'escursione del
segnale, chiamata ampiezza picco-picco (App), il valore efficace,
definito come il valore che dovrebbe essere applicato ad una resistenza pura
per produrre lo stesso effetto termico, il valore medio, ecc...
Questi parametri sono importanti perchè ci consentono di studiare in modo
matematico il comportamento dei circuiti in presenza di tali segnali.
Esaminiamo ora i segnali che più comunemente vengono usati.
-segnali sinusoidali
I segnali sinusoidali sono segnali alternati, cioè con forma d'onda simmetrica
rispetto allo zero (figura), che vengono descritti dalla seguente relazione:
u = Um · sen( w t + j
dove Um è il valore massimo del segnale, w è la pulsazione, che dipende dalla frequenza secondo la relazione w = 2 p f misurata in rad/sec, e j è la fase iniziale.
Il valore efficace U di un segnale sinusoidale vale
|
U = |
Um |
= 0,707·Um |
In figura è riportato l'andamento tipico di un segnale sinusoidale.
|
|
Fig.5: Un tipico segnale sinusoidale |
-segnali ad onda quadra
Questi tipi di segnali rivestono particolare importanza nell'elettronica
digitale e nella trasmissione dati. La figura x rappresenta un tipico segnale
ad onda quadra.
Un parametro importante per questi segnali è il duty cycle (d.c. o d ), che
rappresenta il rapporto percentuale tra il tempo durante il quale il segnale
presenta il suo valore alto ed il periodo totale:
|
d = |
T1 |
|
Il segnale mostrato in figura 6a, presenta un duty cycle
del 50%.
Quando però il duty cycle assume valori differenti dal 50%, si dovrebbe parlare
più propriamente di segnali rettangolari (figura 6b) e, nel caso in cui il
valore sia molto diverso dal 50%, di segnali impulsivi (figura 6c).
|
|
|
|
a) |
b) |
|
|
|
|
c) |
|
|
Fig.6: a) segnale ad onda quadra; b) aegnale rettangolare; c) segnale impulsivo |
|
Come si puo' intuire, il valore medio e il valore efficace di un segnale di questo tipo, dipende anche dal suo duty cycle, e per i segnali che presentano un d.c. del 50% come quello in figura 6a, essi valgono rispettivamente UH/2 e UH/ Ö 2.
-segnali a dente di sega
L'utilizzo dei segnali a dente di sega è molto diffuso in applicazioni come
ricevitori TV, oscilloscopi, circuiti di temporizzazione, ecc... Prendono
questo nome dalla loro forma tipica, come è evidente in figura 7.
|
|
Vari tipi di segnale
Con il termine segnale intendiamo generalmente indicare tensioni o correnti che seguono una certa evoluzione temporale, e che riscontriamo nei circuiti elettrici che esaminiamo. Definiamo poi con il termine forma d'onda l'insieme dei valori istantanei assunti da un segnale.
Esistono vari tipi di segnali, ma comunque tutti
riconducibili a due principali categorie: i segnali periodici e i segnali
aperiodici (o non periodici). Nel primo caso siamo di fronte a un segnale che
si ripete in modo ciclico, ad intervalli di tempo che chiamiamo perido e
indichiamo con T, e che seguono una determinata legge matematica che ne
determina l'andamento.
Il numero di periodi che si ripetono nell'unità di tempo definisce la frequenza
f del segnale, ovvero
|
f = |
1 |
che si misura in hertz (Hz).
Per descrivere le caratteristiche dei segnali periodici si
ricorre alla definizione di alcuni parametri. La frequenza appena citata è uno
di questi, ma vi sono anche per esempio l'ampiezza massima dell'escursione del
segnale, chiamata ampiezza picco-picco (App), il valore efficace,
definito come il valore che dovrebbe essere applicato ad una resistenza pura
per produrre lo stesso effetto termico, il valore medio, ecc...
Questi parametri sono importanti perchè ci consentono di studiare in modo
matematico il comportamento dei circuiti in presenza di tali segnali.
Esaminiamo ora i segnali che più comunemente vengono usati.
-segnali sinusoidali
I segnali sinusoidali sono segnali alternati, cioè con forma d'onda simmetrica
rispetto allo zero (figura), che vengono descritti dalla seguente relazione:
u = Um · sen( w t + j
dove Um è il valore massimo del segnale, w è la pulsazione, che dipende dalla frequenza secondo la relazione w = 2 p f misurata in rad/sec, e j è la fase iniziale.
Il valore efficace U di un segnale sinusoidale vale
|
U = |
Um |
= 0,707·Um |
In figura è riportato l'andamento tipico di un segnale sinusoidale.
|
|
Fig.5: Un tipico segnale sinusoidale |
-segnali ad onda quadra
Questi tipi di segnali rivestono particolare importanza nell'elettronica
digitale e nella trasmissione dati. La figura x rappresenta un tipico segnale
ad onda quadra.
Un parametro importante per questi segnali è il duty cycle (d.c. o d ), che
rappresenta il rapporto percentuale tra il tempo durante il quale il segnale
presenta il suo valore alto ed il periodo totale:
|
d = |
T1 |
|
Il segnale mostrato in figura 6a, presenta un duty cycle
del 50%.
Quando però il duty cycle assume valori differenti dal 50%, si dovrebbe parlare
più propriamente di segnali rettangolari (figura 6b) e, nel caso in cui il
valore sia molto diverso dal 50%, di segnali impulsivi (figura 6c).
|
|
|
|
a) |
b) |
|
|
|
|
c) |
|
|
Fig.6: a) segnale ad onda quadra; b) aegnale rettangolare; c) segnale impulsivo |
|
Come si puo' intuire, il valore medio e il valore efficace di un segnale di questo tipo, dipende anche dal suo duty cycle, e per i segnali che presentano un d.c. del 50% come quello in figura 6a, essi valgono rispettivamente UH/2 e UH/ Ö 2.
-segnali a dente di sega
L'utilizzo dei segnali a dente di sega è molto diffuso in applicazioni come
ricevitori TV, oscilloscopi, circuiti di temporizzazione, ecc... Prendono
questo nome dalla loro forma tipica, come è evidente in figura 7.
|
|
Il partitore di tensione
Molto spesso nella pratica si usa una formula nota come formula del partitore di tensione. Questa è semplicemente una conseguenza della legge di Ohm generalizzata e dei principi di kirchhoff applicati ad un circuito, detto partitore di tensione, come quello di figura 11
|
|
Fig.11: Un semplice partitore di tensione |
Il nome stesso suggerisce il comportamento del circuito,
cioè quello di "partizionare" la tensione V, ai capi delle due
resistenze, in due tensioni V1 e V2.
Tramite kirchhoff scriviamo l'equazione alla maglia
V - V1 - V2 = 0
da cui
V = R1I + R2I
e poichè la corrente I vale
|
I = |
V |
si ha che
|
V = V |
R1 |
+ V |
R2 |
appare quindi chiaro che V1 e V2 valgono rispettivamente
|
V1 = V |
R1 |
|
V2 = V |
R2 |
che rappresentano, appunto, la formula del partitore di
tensione.
Ciò significa che per calcolare la tensione VR su una resistenza R
facente parte di una serie di resistenze sottoposte a tensione V, è sufficiente
moltiplicare V per il rapporto tra la resistenza stessa e la resistenza totale
del circuito.
Teorema della sovrapposizione degli effetti
-La risposta di una rete lineare alla sollecitazione di più generatori di
tensione o di corrente, equivale alla somma delle risposte causate da ciascun
generatore considerato singolarmente.
Ciò significa che per risolvere una rete elettrica composta
da più generatori, possiamo calcolarne la risposta per ogni singolo generatore
ed infine sommare algebricamente i risultati ottenuti.
Considerare un generatore alla volta significa annullare l'energia introdotta
dagli altri, e cioè considerare nulla la tensione per i generatori di tensione
(che equivale a dire un cortocircuito) e considerare nulla la corrente per i
generatori di corrente (che equivale a dire un circuito aperto).
Prendiamo ad esempio il circuito di figura 12, composto da un generatore di tensione V, un generatore di corrente I, e quattro resistenze R1, R2, R3, R4.
|
|
|
Fig.12 |
Possiamo applicare il teorema della sovrapposizione degli effetti considerando
prima gli effetti del generatore di tensione, poi gli effetti del generatore di
corrente ed infine sommando algebricamente i due risultati per ottenere i valori
delle correnti e delle tensioni del circuito.
Abbiamo detto che i generatori di corrente, quando non considerati, si
traducono in circuiti aperti, quindi, considerando in un primo tempo solamente
il generatore di tensione, il circuito diventa quello di figura 13.
|
|
Fig.13 |
E' evidente che V4 è uguale a zero, dato che in un circuito aperto
non circola corrente. Quindi rimangono solo R1, R2 e R3
in serie al generatore di tensione, perciò la corrente I'1
(coincidente con I'2) vale
|
I'1 = |
V |
= 7,4 mA |
A questo punto passiamo a considerare solo il generatore di corrente cortocircuitando il generatore di tensione, ottenendo così il circuito di figura 14.
|
Fig.14 |
|
Quì il circuito è un po' più complesso. Possiamo allora calcolare la tensione
tra i nodi A e B, e poi ricavare le correnti I''1 e I''2
|
VAB = - ( (R1+R3) // R2 ) · I = - |
(R1+R3)·R2 |
·I = -700 V |
|
I''1 = - |
VAB |
= 666 mA |
|
I''2 = |
VAB |
= -2333,3 mA |
A questo punto sommiamo algebricamente le correnti
I1 = I'1 + I''1 =
7,4+666,6 = 674 mA
I2 = I'2 + I''2 = 0-2333,3 = -2333,3 mA
Appare chiaro che la I2 ha verso opposto a
quello ipotizzato (e quindi anche la V2).
Ora possiamo ricavare tutte le tensioni
V1 = R1·I1 = 33,7 V
V2 = R2·I2 = -699,99 V
V3 = R3·I1 = 674 V
V4 = R4·I = 60 V
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025