CARICA ELETTRICA - CORRENTE ELETTRICA

Ogni grandezza elettrica si abbrevia con una lettera dell'alfabeto. Usiamo la lettera I per indicare la corrente. Esempio volendo dire che vi è una corrente di 10 Ampere scriviamo: I = 10 A, che vuol dire che vi è la corrente I che ha il valore di 10 ampere. Lo strumento che misura la corrente si dice amperometro.

Per la corrente vi sono multipli e sottomultipli, come nella seguente tabella.

I materiali esistenti in natura, li possiamo dividere in conduttori e in isolanti. Materiali conduttori sono quelli che consentono il passaggio della corrente elettrica. Sono conduttori l'argento, il rame, l'oro, l'alluminio, il ferro, l'acqua. Si dicono isolanti i materiali che non consentono il passaggio della corrente elettrica; sono isolanti il marmo, il legno, la gomma, le materie plastiche, la bachelite, il vetro, la carta.

Per far muovere le cariche elettriche occorre una certa forza. Un componente in grado di far muovere le cariche elettriche si dice generatore di tensione. Una pila è un generatore di tensione. Una batteria dell'auto è un generatore di tensione. La tensione si misura in volt, che si abbrevia con la lettera V. La tensione di solito la indichiamo con la lettera E. Esempio E = 12 V, vuol dire che esiste una tensione E, che ha il valore di 12 volt. Lo strumento che misura la tensione elettrica si dice voltmetro.

Per la tensione vi sono multipli e sottomultipli, come nella seguente tabella.

Il generatore di tensione è in grado di separare le cariche elettriche, facendo in modo che tutte le cariche elettriche positive si trovino da un lato del generatore, invece tutte le cariche elettriche negative si trovano dal lato opposto del generatore.

Possiamo notare una pila stilo da 1,5 V, col polo positivo verso l'alto; e una pila a ossido di argento col positivo sul lato posteriore. (I marchi visibili sono di proprietà delle relative ditte costruttrici)

Il simbolo del generatore di tensione è il seguente.

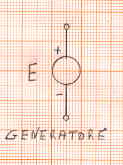
Si dice morsetto o polo del generatore una delle due parti terminali di un generatore di tensione. Quindi il generatore ha due morsetti. Il morsetto si indica col simbolo:

Nel generatore vi è un morsetto positivo, che indichiamo col segno +, dove sono concentrate solo cariche positive. Vi è inoltre un morsetto negativo, che indichiamo col segno , dove sono concentrate tutte le cariche negative.

CIRCUITO ELETTRICO

Si dice circuito elettrico un percorso chiuso, partendo da un punto qualsiasi e tornando allo stesso punto. Ovviamente nel circuito vi deve essere almeno un componente elettrico. Il generatore di tensione è un componente elettrico. Una lampada è un componente elettrico e si indica col simbolo.

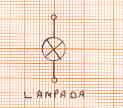
Un interruttore è un componente elettrico, e si indica col simbolo.

Se l'interruttore è aperto

non passa corrente.

Se l'interruttore è chiuso la corrente passa. Quindi dato un semplice circuito:

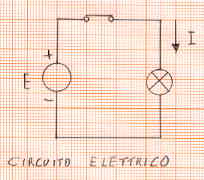
composto da generatore di tensione, interruttore e lampada, quando l'interruttore è chiuso nel circuito circola una certa corrente e la lampada si accende. Quando l'interruttore è aperto la corrente non può circolare nel circuito e la lampada si spegne. La linea che unisce i vari componenti rappresenta il filo elettrico. Il filo elettrico è fatto di rame, che è un materiale conduttore; l'esterno del filo è rivestito di materiale isolante, di solito polivinilcloruro, per evitare pericoli per l'utente.

RESISTENZA

Quando la corrente circola in un circuito incontra un certo ostacolo durante il percorso. Vale a dire che nonostante percorre il circuito alla velocità della luce, la corrente che può passare dipende da come è costruito il componente, cioè dalla sua lunghezza, dalla sua sezione, dal materiale utilizzato. Si dice resistenza di un componente elettrico l'ostacolo che esso oppone al passaggio della corrente elettrica. Unità di misura della resistenza è l'ohm, che si abbrevia col simbolo  , che si legge ohm. La resistenza di solito la indichiamo con la lettera R. Esempio R= 1.000  , vuol dire che esiste una resistenza R, che ha il valore di 1.000 ohm. Lo strumento che misura la resistenza si dice ohmmetro.

Per la resistenza esistono i multipli, secondo la seguente tabella:

Notiamo, da sinistra, un resistore a filo da 50  un resistore ad impasto, un resistore variabile, detto potenziometro.

Ricordiamo che resistore è un componente, resistenza è la proprietà che ha il resistore. 

Il simbolo elettrico del resistore è:

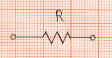
La resistenza di un filo si calcola con la seguente formula:

R = L

   S

Dove R è la resistenza, misurata in  ,  è la resistività del materiale misurata in ^mm² / m , L è la lunghezza del filo misurata in metri, S è la sezione del filo misurata in mm². Il  del rame è 0,0177 ^mm² / m. Ogni materiale ha la sua resistività. Un buon conduttore ha una bassa resistività, cioè oppone poca resistenza al passaggio della corrente, invece un isolante ha una elevata resistività.

LEGGE DI OHM

La legge di Ohm è una legge fondamentale dell'elettrotecnica. Essa indica la relazione fra la tensione e la corrente di un qualunque componente elettrico. La formula è la seguente:

V = R I

Dove V è la tensione ai capi del componente considerato, R è la resistenza del componente, I è la corrente del componente. Tale formula ci dice che vi è una proporzionalità diretta tra tensione e corrente del componente. Infatti, tenendo costante la resistenza del componente, all'aumentare della tensione applicata ai capi del componente aumenta la corrente che circola nel componente stesso.

Campo magnetico

E' così chiamato il campo di forza prodotto da un magnete, oppure da una corrente elettrica, oppure da un campo elettrico variabile nel tempo. Con campo magnetico si intende anche la grandezza fisica, simbolo H [A / m] , che indica la forza che agisce nel campo su un polo magnetico di intensità unitaria.

Cominciamo col prendere in considerazione il campo magnetico generato da un magnete avente forma di barretta. Si possono individuare due poli, più precisamente il polo Nord dal quale escono le linee di forza del campo magnetico ed il polo Sud nel quale entrano le linee di forza del campo magnetico. Si osserva che, a differenza dei campi elettrici, nel caso dei campi magnetici le linee di forza sono chiuse. I due poli sono così chiamati perché, se il magnete è lasciato libero di orientarsi nello spazio, rivolge sempre l'estremità individuata come polo Nord verso il Nord geografico e l'altra verso il Sud geografico. Ciò accade perché la Terra è per sua natura un gigantesco magnete, avente il polo Sud magnetico quasi in corrispondenza del polo Nord geografico, che agisce nello spazio circostante attraverso un suo campo magnetico e due magneti tendono ad attrarsi se sono affacciati coi poli opposti.

Una ulteriore proprietà dei magneti è quella che, se sminuzzati, tendono a formare ulteriori magneti di dimensioni più piccole, questo perché i poli magnetici Nord e Sud non possono essere divisi in alcun modo.

Ancora si deve dire che i materiali ferrosi, se avvicinati ad un magnete in modo tale da entrare nel suo campo magnetico, subiscono il fenomeno della magnetizzazione, ovvero anche essi diventano magnetici e presentano dal lato col quale sono accostati una polarità magnetica opposta a quella del magnete permanente. Questo è il motivo per il quale il ferro viene attratto dai magneti. Se poi i materiali ferrosi sono allontanati dal campo magnetico del magnete permanente accade che essi perdono quasi tutto il magnetismo precedentemente acquisito.

Prendiamo ora in considerazione il campo magnetico prodotto dalle correnti elettriche

In un conduttore rettilineo percorso da una corrente di intensità I, il campo magnetico nello spazio circostante avrà le linee di forza come in figura e la sua intensità in un punto distante d dalla corrente varrà H = I / (2··d) [A /m] ( legge di Biot-Savart ).

Consideriamo come ulteriore esempio un solenoide (avvolgimento avente forma di bobina), di lunghezza l molto maggiore del diametro, composto di N spire e percorso dalla corrente di intensità I . Per tale sistema si può dire che il campo all'interno è praticamente uniforme e di intensità H = N·I / l [A / m] .

Infine consideriamo un solenoide toroidale la cui principale caratteristica è quella di contenere tutto il campo al proprio i 212b17c nterno. Se N è il numero di spire, r è la lunghezza del raggio medio ed I l'intensità della corrente, sarà H = N·I / (2··r) [A / m] .

In ogni caso, qualsiasi sia il circuito, tra il verso della corrente nel circuito ed il verso del campo magnetico generato dalla corrente, esiste sempre la stessa relazione che si riscontra tra il verso di rotazione di una vite ed il verso di avanzamento della vite stessa.

Induzione magnetica, permeabilità magnatica

Gli effetti dovuti alla presenza di campo magnetico dipendono, oltre che dal valore del campo, anche dalla natura del mezzo entro il quale il campo si sviluppa. Rispetto al loro comportamento nei confronti dei campi magnetici, le sostanze si possono classificare in :

diamagnetiche pure : sono così chiamate perché presentano solo diamagnetismo (proprietà riconducibile alla precessione di Larmor degli elettroni nel campo magnetico, comune a tutte le sostanze). Il diamagnetismo è indipendente dallo stato fisico del mezzo, tali sostanze si magnetizzano solo in presenza di un campo magnetico esterno assumendo una polarità opposta a quella del campo esterno. Per tale motivo, in un campo magnetico non omogeneo, agisce su di un corpo diamagnetico una forza che cerca di spingerlo fuori dal campo magnetico, mentre in un campo magnetico omogeneo la presenza di un corpo diamagnetico produce la deformazione delle linee di campo rappresentata in figura. Sono sostanze diamagnetiche i gas nobili, l'azoto, l'idrogeno, la grafite, l'oro, la salgemma e l'acqua.

paramagnetiche : sono così chiamate quelle sostanze che, a causa della presenza di livelli elettronici non chiusi, tendono a costituire molecole magneticamente dipolari (assimilabili a magnetini elementari). Per tali sostanze la magnetizzazione provocata da un campo magnetico esterno è in linea e concorde con questo e le sostanze paramagnetiche vengono attirate da un campo esterno non omogeneo verso le zone con maggiore intensità di campo. In un campo magnetico omogeneo la presenza di un corpo paramagnetico produce la deformazione delle linee di campo rappresentata in figura. Il paramagnetismo diminuisce coll'aumentare della temperatura e già alla temperatura ambiente i magnetini elementari si trovano in disordine statistico a causa del movimento termico. Sono sostanze paramagnetiche l'alluminio, il magnesio, il manganese, il cromo, il sodio, il potassio, l'ossigeno e l'aria.

ferromagnetiche : sono così chiamate quelle sostanze che, a causa del loro particolare stato cristallino, presentano delle aree con magnetizzazione costante (domini di Weiss) nelle quali i magnetini elementari sono orientati parallelamente tra di loro. Godono delle stesse proprietà dei materiali paramagnetici con l'aggiunta di poter essere, già alla temperatura ambiente, loro stesse sorgenti di campo magnetico qualora siano state precedentemente immerse in un campo magnetico. Le sostanze ferromagnetiche perdono le loro proprietà e diventano paramagnetiche se sottoposte ad una temperatura uguale o maggiore alla temperatura di Curie ( 768 [°C] per il ferro). Sono sostanze ferromagnetiche il ferro, il nickel, il cobalto e speciali leghe.

Nelle sostanze ferromagnetiche la tendenza a "catturare" le linee di campo magnetico, propria anche delle sostanze paramagnetiche, è particolarmente accentuata (vedi figura). Tale fatto viene utilizzato al fine di creare degli schermi magnetici che rendono lo spazio al loro interno praticamente insensibile ai campi magnetici esterni. Sono varie le applicazioni degli schermi magnetici, ad esempio in alcuni strumenti la schermatura serve ad evitare che il campo magnetico terrestre od i campi magnetici spuri prodotti nel laboratorio possano alterare i valori misurati.

Si chiama induzione magnetica (o densità di flusso magnetico) il vettore associato al campo magnetico la cui grandezza rappresenta una misura dell'intensità dell'azione di un campo magnetico; in essa viene compreso l'influsso del materiale attraversato dal campo e del relativo stato di magnetizzazione. Così che l'induzione magnetica, a parità di campo magnetico inducente, ad esempio è maggiore nel ferro piuttosto che nell'aria:

B = ·H [Wb / m²] , nel vuoto si ha o = 1,257·10^-6 [H / m]

Per i mezzi diversi dal vuoto, la permeabilità magnetica assoluta si esprime relativamente a quella del vuoto r · o dove r è un numero puro chiamato permeabilità relativa. Per le sostanze diamagnetiche si ha che r è di pochissimo inferiore ad uno, per le sostanze paramagnetiche r è di pochissimo superiore ad uno, per le sostanze ferromagnetiche r è di molto più grande di uno (può arrivare anche a 100.000).

Induttanza elettrica di un circuito

E', più correttamente, chiamata coefficiente di autoinduzione. Rappresenta l'attitudine di un circuito elettrico a concatenarsi col flusso di campo magnetico ac originato dalla corrente elettrica I che percorre il circuito stesso :

L = ac / I [H]

Tale parametro dipende dalla forma e dalle dimensioni geometriche del circuito elettrico oltre che dalla permeabilità magnetica  del mezzo entro il quale si sviluppa il campo magnetico prodotto dalla corrente che percorre il circuito stesso. Tende ad essere grande per i circuiti con forma ad avvolgimento ed avvolti su nuclei ferromagnetici. Ad esempio, per un solenoide rettilineo di lunghezza l superiore di almeno 10 volte del diametro, di sezione S e composto da N spire, l'induttanza vale :

L = ·S·N² / l [H]

La stessa espressione vale pure per il solenoide toroidale già visto.

I dispositivi che realizzano valori concentrati elevati di induttanza sono chiamati induttori. Possono essere collegati in serie od in parallelo, se collegati in serie l'induttanza complessiva è pari alla somma delle singole induttanze, se collegati in parallelo l'inverso dell'induttanza complessiva è pari alla somma degli inversi delle singole induttanze.

Legge generale dell'induzione elettromagnetica

E' alla base del principio di funzionamento di gran parte delle macchine e applicazioni elettriche (generatori, motori, trasduttori, ecc.) e prende anche il nome di legge di Faraday-Neuman-Lenz. Essa dice che ogniqualvolta varia nel tempo il flusso concatenato con un circuito elettrico, nel circuito elettrico scaturisce una forza elettromotrice indotta di intensità proporzionale alla velocità di variazione del flusso concatenato.

Con riferimento ad un intervallo finito di tempo t , il valore medio della f.e.m.i. vale :

Il verso della f.e.m.i. è tale da opporsi alla variazione di flusso concatenato che l'ha generata, ovvero se nel circuito, grazie alla e_{i ,} può circolare una corrente essa avrà verso tale da dar luogo ad un campo magnetico concorde con quello concatenato che sta variando se questi sta diminuendo, opposto se questi sta aumentando.

Se il flusso concatenato che varia è quello dovuto alla induttanza stessa del circuito elettrico, si parla di forza elettromotrice autoindotta :

Quale esempio consideriamo quello del circuito di figura, costituito da tre lati indeformabili ed un lato MN di lunghezza l che può scorrere verticalmente. Supponiamo che tale movimento avvenga senza attrito. Sia R la resistenza complessiva de circuito. Il circuito sia concatenato con un campo magnetico di induzione B uniforme, le cui linee di forza siano perpendicolari ed entranti nel piano su cui giace il circuito. Si consideri il lato MN in movimento verso il basso con una velocità costante ve . Se all'istante t la posizione occupata dal lato in movimento è quella indicata a tratto pieno,dopo un intervallo di tempo t , e quindi all'istante (t + t) , la posizione occupata sarà quella indicata in tratteggio essendo lo spazio percorso x = ve·t . Nell'intervallo di tempo t , a causa dell'aumento della superficie del circuito intersecata dalle linee di campo magnetico, sarà aumentato il flusso concatenato di una quantità pari a c = B·l·x e, quindi, per la legge generale della induzione elettromagnetica si sarà sviluppata una f.e.m.i. di valore :

Il verso di tale f.e.m.i. dovrà essere tale da opporsi alla variazione di flusso concatenato e, quindi, considerando che il flusso concatenato aumenta, la e_i dovrà tendere a far circolare una corrente da M verso N così che il flusso generato da tale corrente si opponga a quello preesistente dovuto all'induzione B . Molto semplicemente il verso della f.e.m.i. si può determinare con la regola delle tre dita della mano destra, orientate a formare una terna cartesiana ortogonale ( col pollice nel verso della velocità del conduttore rispetto al campo, l'indice nel verso dell'induzione magnetica, il medio nel verso della f.e.m.i.).

Nel caso in cui il conduttore di lunghezza l sia soggetto ad una velocità formante un generico angolo  con l'asse del conduttore stesso, sarà:

Circuiti magnetici, legge di Hopkinson

Si chiama tubo di flusso del vettore induzione magnetica lo spazio tubolare racchiuso dalla superficie descritta dalle linee di forza passanti per i punti di una qualsiasi linea chiusa tracciata nel campo.

Si definisce circuito magnetico una qualunque regione dello spazio costituita da un tubo di flusso del vettore induzione magnetica. Un tronco di circuito magnetico si dice omogeneo se in esso sono costanti la sezione, la permeabilità magnetica e l'induzione magnetica.

Considerando un circuito magnetico composto da k tronchi omogenei sui quali agiscono m avvolgimenti, la legge di Hopkinson afferma che:

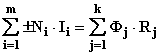
dove:

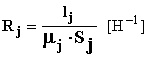
è chiamata riluttanza magnetica.

Nelle espressioni sopra scritte, con lj si intende la lunghezza del tronco generico j misurata in [m] e con Sj la sua sezione misurata in [m ²].

La legge di Hopkinson viene usata per il calcolo dei circuiti magnetici mediante il metodo delle riluttanze. Tale legge è analoga formalmente alla legge di Ohm per i circuiti elettrici. L'analogia riveste notevole importanza in quanto si mantengono formalmente valide, con le opportune schematizzazioni, le leggi relative ai collegamenti delle resistenze elettriche ed i due principi di Kirchhoff con le seguenti corrispondenze:

intensità di corrente I [A]  flusso  [Wb]

densità di corrente  [A/m²] campo magnetico B [Wb/m²]

f.e.m. Eo [V] forza magnetomotrice N·I [A]

resistenza elettrica R [] riluttanza magnetica R [H^-1]

caduta di tensione R·I [V] caduta di tensione magnetica R·= H·l [A]

d.d.p. V_MN [V] tensione magnetica (H·l)_MN [A]

resistività elettrica  [·m] inverso della permeabilità magnetica, ^ [H^-1·m]

Circuiti magnetici a più maglie

La risoluzione dei circuiti magnetici è relativamente semplice se i circuiti sono del tipo tutto serie (ovvero con i tronchi omogenei che si succedono l'uno all'altro così che il flusso sia costante in tutte le sezioni del circuito).

Nel caso di circuiti formati da più maglie, ovvero con tronchi percorsi da flussi anche tra di loro diversi, la risoluzione è alquanto più complessa. Capita infatti che anche nel caso di problemi del tipo diretto, a causa della non linearità del mezzo ferromagnetico non si possa prevedere il flusso nei vari rami e, quindi, si debba procedere per tentavi. Solo la presenza di simmetrie nel circuito può, in certi casi, semplificare la risoluzione permettendo il calcolo diretto dei flussi nei vari rami.

Tensione magnetica, legge della circuitazione magnetica

Si consideri una linea di campo magnetico e si individuino diversi tratti l per ciascuno dei quali si possano ritenere costanti la permeabilità magnetica, il campo magnetico e, quindi, l'induzione magnetica.

Per ciascuno di questi tratti, il prodotto H·l [A] viene chiamato tensione magnetica (per analogia col caso elettrostatico, ove il prodotto del campo elettrico per la lunghezza fornisce una tensione elettrica). Se si desidera la tensione magnetica tra i punti M e K si dovrà considerare:

(H·l)_MH = H₁·l₁ + H₂·l₂ + H₃·l₃

La legge della circuitazione (nota anche come legge di Ampere) dice che se si estende la sommatoria all'intera linea chiusa di campo magnetico si ha :

H₁·l₁ + H₂·l₂ + H₃·l₃ + . . . = N·I

dove N rappresenta il numero di volte per il quale la linea di campo magnetico di concatena col circuito percorso dalla corrente di intensità I .

Se la stessa linea di forza è concatenata con più circuiti elettrici si avrà :

H₁·l₁ + H₂·l₂ + H₃·l₃ + . . . = ± Na·Ia ± Nb·Ib ± Nc·Ic ± . . .

dove a , b , c , . . . sono i vari circuiti concatenati con la stessa linea di forza. I vari termini ± N·I [A] si chiamano forze magnetomotrici (per analogia con le forze elettromotrici dei circuiti elettrici). Le forze magnetomotrici si assumono positive se favoriscono un campo magnetico concorde col verso della linea chiusa, altrimenti si considerano negative.

Introduzione, legge di Coulomb

Quanto esposto in questi appunti ha lo scopo di riassumere quelle conoscenze della elettrostatica già note dal corso di fisica del biennio e di proporre quelle integrazioni che più direttamente fanno riferimento alle applicazioni elettrotecniche. Nelle espressioni, le grandezze vettoriali sono indicate mediante sottolineatura.

Con elettrostatica si intende la teoria che studia l'effetto di forza dovuto a cariche elettriche immobili.

Si chiama carica elettrica la quantità di elettricità positiva o negativa di un corpo, essa è sempre un multiplo intero della carica elementare (quanto elementare) e = 1,602·10^-19 [C] (la più piccola quantità di carica elettrica esistente è la carica dell'elettrone, pari a -e ).

Una delle proprietà più importanti delle cariche elettriche è descritta dalla legge di Coulomb : la forza elettrica F di attrazione (cariche di segno opposto) o di repulsione (cariche di uguale segno) fra due cariche puntiformi Q₁ e Q₂ immerse in un mezzo isolante è proporzionale al prodotto delle cariche ed inversamente proporzionale al quadrato della loro distanza :

La direzione della forza è la retta passante per le due cariche. La grandezza  è chiamata costante dielettrica assoluta delmezzo isolante e, per il vuoto, essa vale :

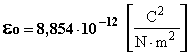
Per un mezzo diverso dal vuoto si è soliti esprimerla come prodotto tra la costante dielettrica del vuoto e la costante dielettrica relativa del mezzo  = o · r .

Campo elettrico

E' così chiamata ogni regione dello spazio ove si esercitano forze elettriche su cariche elettriche. Il campo elettrico è determinato in ogni punto dalla grandezza vettoriale E , quindi è definito in ogni punto da una intensità, una direzione ed un verso. L'intensità, la direzione ed il verso sono pari a quelli della forza elettrica che agisce su un'unità di carica positiva posta in quel punto. Se ne ha una rappresentazione visibile mediante le linee di forza e le superfici equipotenziali. Le linee di forza sono linee orientate secondo il verso di E le cui tangenti coincidono in ogni punto del campo con la direzione del vettore E .

Con potenziale di un punto del campo elettrico si intende il valore di energia potenziale che l'unità di carica positiva possiede in quel punto. Si sceglie a piacere un punto come punto zero dell'energia potenziale. I punti di eguale potenziale sono posti su superfici equipotenziali, tali superfici sono perpendicolari alle linee di forza. Una carica elettrica positiva può essere mossa su di una superficie equipotenziale senza perdita ne guadagno di energia, mentre per essere mossa da una superficie a minor potenziale verso una a maggior potenziale richiede un lavoro che, infine, si ritrova sotto forma di maggior energia potenziale posseduta dalla carica. Qualunque carica positiva collocata in un punto del campo elettrico tende a muoversi nel verso della linea di forza passante per quel punto, così facendo vede diminuire il proprio potenziale.

Si definisce differenza di potenziale tra due punti M, N del campo elettrico la differenza tra il potenziale nel primo punto ed il potenziale nel secondo punto : V_MN = V_M - V_N .

Nota Bene.: quello di campo è un concetto fondamentale per la descrizione di stati ed effetti nello spazio, risalente a Faraday. I campi di forza (campi vettoriali), quali quelli di forza elettrica, di forza magnetica, di forza gravitazionale, sono definiti dalla intensità, dalla direzione e dal verso di una forza per ogni punto dello spazio. I campi scalari indicano invece la distribuzione nello spazio di valori numerici, ad esempio di temperatura o densità.

Se in un punto dello spazio caratterizzato da una intensità di campo elettrico pari ad E vi è una carica pari a Q, si avrà agente sulla carica una forza elettrica pari a F = E·Q , da cui si ricava che l'unità di misura del campo elettrico è il [N / C] . La direzione di questa forza è la stessa del campo, il verso è quello del campo se la carica è positiva, altrimenti è ad esso opposto.

Il potenziale elettrico, essendo un'energia per unità di carica, si misura in [J/C]. Così è pure per la differenza di potenziale. Se in un punto di un campo elettrico ove il potenziale vale V è presente una carica Q , tale carica possederà una energia potenziale elettrica pari a W = Q·V [Joule]. Il [J/C] è chiamato volt [V].

Consideriamo ora un campo elettrico stazionario (cioè non variabile nel tempo) ed uniforme (cioè non variabile al variare del punto considerato). Prendiamo due punti M, N sulla stessa linea di forza, distanti tra di loro d , ed immaginiamo una carica positiva Q che passi dal punto M al punto N . Tale carica perderà energia potenziale e compirà un lavoro se V_M > V_N perché sarà la forza elettrica a determinarne lo spostamento, viceversa acquisterà energia potenziale e su di essa bisognerà compiere un lavoro se V_M < V_N perché si dovrà vincere la forza elettrica con una forza esterna. In ogni caso, per il principio di conservazione dell'energia, dovrà essere il lavoro uguale alla variazione di energia potenziale :

F·d = Q·V_M - Q·V_N = Q·V_MN  E·Q·d = Q·V_MN 

La situazione appena descritta è quella che si verifica nel dielettrico (isolante) posto tra le armature piane e parallele di un condensatore.

Nel caso di campi elettrici non uniformi, quanto detto rimane ancora valido solo che si dovranno considerare punti M ed N a distanza tra di loro talmente piccola da potersi ritenere in tale tratto uniforme il campo.

Per i campi elettrici si può inoltre dire che il lavoro connesso al movimento di una carica tra due punti M ed N (situati anche su diverse linee di forza) non dipende dal percorso seguito dalla carica per passare da M ad N , ma dipende solo dalla posizione dei punti M ed N ( i campi che godono di tale proprietà sono detti campi conservativi e tale è anche il campo gravitazionale

Condensatore elettrico

E' così chiamato il dispositivo atto a realizzare un adeguato valore concentrato di capacità elettrica. Per capacità elettrica si intende l'attitudine di un circuito ad accumulare carica elettrica. La capacità elettrica è definita dalla legge C = Q / V e si misura in [Farad]. Un condensatore si realizza generalmente mediante due superfici di materiale conduttore con interposto un mezzo dielettrico (isolante). Applicando una differenza di potenziale tra le armature si crea un campo elettrico nel dielettrico e, grazie al lavoro del generatore, un accumulo di carica sulle stesse (carica positiva sull'una e negativa sull'altra), tanto più grande quanto più è grande la capacità del condensatore. Una volta che il condensatore si è caricato, per i circuiti in corrente continua si ha che nel ramo ove è inserito il condensatore non può più passare la corrente elettrica.

La capacità di un condensatore ad armature piane e parallele dipende dalla superficie delle armature S [m²], dalla loro distanza d [m] e dalla costante dielettrica del dielettrico interposto e [F/m] secondo la seguente relazione:

Se si hanno diversi condensatori in parallelo, ovvero sottoposti alla stessa differenza di potenziale, la capacità totale è pari alla somma aritmetica delle singole capacità:

si hanno diversi condensatori in serie, ovvero tutti aventi la stessa quantità di carica elettrica, la capacità totale è pari all'inverso della somma aritmetica degli inversi delle singole capacità:

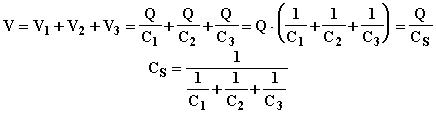
Anche per i condensatori sono possibili le trasformazioni triangolo - stella e viceversa così come per le resistenze. Le relazioni da usare sono le seguenti:

Comportamento elettrostatico dei corpi conduttori

Nei corpi conduttori elettrizzati (cioè che abbiano acquisito carica elettrica, ad esempio sotto forma di elettroni se si tratta di metalli) si verifica quanto segue :

a) in condizione di equilibrio le cariche elettriche libere sono distribuite unicamente sulla superficie esterna del corpo conduttore perché, data la mobilità delle cariche elettriche libere, le interazioni coulombiane che si esercitano tra di esse, essendo le cariche libere tutte dello stesso segno, portano tutte le cariche a raggiungere la superficie limite del corpo conduttore.

b) le cariche elettriche libere in equilibrio sulla superficie del conduttore devono assumere una distribuzione tale che il potenziale di ciascun punto P1 , P2 , P3 , ecc. rispetto ad un riferimento O sia sempre lo stesso, ovvero V_P1 = V_P2 = V_P3 = ecc. Si dice così che la superficie è equipotenziale. Se fosse diversamente avremmo tra due punti, ad esempio P1 e P2 , una differenza di potenziale che provocherebbe uno spostamento degli elettroni liberi verso il punto a potenziale maggiore, contraddicendo così la condizione di equilibrio statico.

c)le cariche elettriche libere in equilibrio sulla superficie dei conduttori producono un campo elettrico E sempre perpendicolare alla superficie stessa del conduttore, se così non fosse si avrebbe, oltre alla componente normale En , una componente tangenziale Et a causa della quale una carica elettrica libera superficiale Q si muoverebbe essendo sotto l'azione di una forza elettrica Ft = Et·Q la qual cosa contraddice la condizione di equilibrio statico.

d) il campo elettrico all'interno di un corpo conduttore in equilibrio statico è sempre nullo in quanto, se fosse diverso da zero, gli elettroni liberi sarebbero in movimento la qual cosa contraddice la condizione di equilibrio statico. Ne risulta in particolare che l'equilibrio elettrico di un conduttore elettrizzato non viene alterato se si immagina di scavare internamente il conduttore stesso fino a ridurlo ad un involucro, anche sottilissimo, costituito da una pellicola metallica corrispondente alla superficie esterna. Nei fenomeni elettrostatici, quindi, il comportamento di un conduttore massiccio non differisce da quello di un conduttore internamente cavo avente eguale forma e dimensioni. Nell'interno di questi conduttori cavi (praticamente sono degli involucri metallici) il campo elettrico rimane sempre nullo , qualunque sia la carica elettrica distribuita sulla superficie esterna, e cioè qualunque sia l'intensità del campo elettrico nello spazio esterno al conduttore cavo. Si intende che, se nell'interno dell'involucro sono racchiusi dei conduttori isolati dalle pareti del l'involucro ed elettrizzati, questi vi producono un campo elettrico il quale rimane del tutto indipendente da tutte le eventuali cariche elettriche situate all'esterno. Si può dire che un involucro metallico completamente chiuso costituisce uno schermo elettrostatico che protegge l'intera regione interna dalle azioni di tutti i campi elettrici esterni (schermo di Faraday).

Induzione elettrostatica e spostamento elettrico

Per induzione elettrostatica si intende l'azione di un campo elettrico esterno su un conduttore isolato. Le cariche elettriche alla superficie vengono separate dalle forze di Coulomb. Poiché il bilancio di carica del conduttore non è alterato dall'induzione, il conduttore resta nel complesso elettricamente neutro.

Con spostamento dielettrico (eccitazione dielettrica) si intende il vettore D = ·E , esso corrisponde alla carica prodotta nell'unità di superficie per induzione elettrostatica e si misura in [C / m²] .

Unità Elettrotecniche

Multipli e Sottomultipli

La legge di Ohm

La legge di ohm stabilisce una diretta proporzionalità tra corrente e tensione.

V = R * I

R = V / I

I = V / R

Sistemi di Distribuzione

I sistemi di distribuzione vengono identificati con delle lettere:

Prima lettera

- situazione del sistema elettrico di alimentazione rispetto alla terra

Seconda lettera

- situazione delle masse dell'impianto rispetto alla terra

Lettere successive

- situazione dei conduttori di neutro (N) e di protezione (PE)

Designazione dei componenti degli equipaggiamenti elettrici delle macchine industriali

(CEI 44-6)

Tensioni Standard in Italia

• Sistemi monofasi
• 230 V in corrente alternata 50 Hz
• Sistemi trifase
• 400 V in corrente alternata 50 Hz

Correnti Continue e Alternate

Correnti continue

• Caratterizzate dall'avere i valori di corrente e tensione definiti da un valore preciso, costante nel tempo.

Correnti alternate

• Valore istantaneo: e il valore che assume la grandezza in un determinato istante, si indica con una lettera minuscola (es. i per la corrente o u per la tensione)
• Valore massiomo o di picco o di cresta A_M é il valore massimo che la grandezza può assumere (può essere sia positivo che negativo)
• Valore efficace (RMS) A: è il valore che dovrebbe avere una corrente continua per produrre gli stessi effetti termici; e corrisponde a:

A = A_M / = 0.707 A_M

• Periodo T: è l'intervallo di tempo che intercorre fra l'istante in cui la grandezza assume un dato valore e la successiva volta che assume lo stesso valore, dopo aver assunto tutti i valori possibili sia negativi che positivi.
• Frequenza f: è il numero di periodi che si verificano in un secondo, e risulta pari a:

f = 1 / T

• Pulsazione: esprime la velocità angolare (in radianti al secondo) del vettore ( di ampiezza A_M ) che con la sua rotazione genera la sinusoide.

= 2 / T = 2 f t

Trasformatori e Autotrasformatori

• Il trasformatore è una macchina statica funzionante solo in corrente alternata, in grado di trasformare un sistema di corrente e tensione in un altro sistema con differenti valori di corrente e tensione.
• I trasformatori possosno essere sia monofasi che trifasi

Classi di Isolamento

Collegamenti principali

Motori

Motori ad una velocità

Gli avvolgimenti dei motori standar possono essere collegati nei due modi sotto indicati:

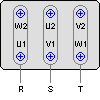
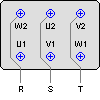
Collegamento a Stella

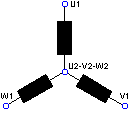
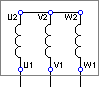
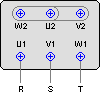
La tensione sugli avvolgimenti corrisponde: V_ph = V_n

La corrente che scorre sugli avvolgimenti corrisponde: I_ph = I_n

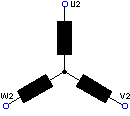
Collegamento a Triangolo

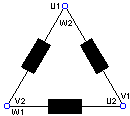
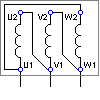
La tensione sugli avvolgimenti corrisponde: V_ph = V_n

La corrente che scorre sugli avvolgimenti corrisponde: I_ph = I_n

Numero poli: 2,4,6,8 ...

Velocita di sincronismo a 50 Hz (giri/min): 3000, 1500, 1000, 750 ...

Esempio di collegamento

Collegamento per motori a due velocità con due avvolgimenti

Velocità alta

Velocità bassa

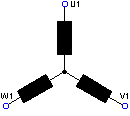
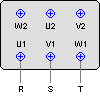
Numero poli: 2/6, 2/8, 4/6, 6/8

Velocita di sincronismo a 50 Hz (giri/min): 3000/1000, 3000/750, 1500/1000, 1000/750

Collegamento Dahander per motori a due velocità a coppia costante

velocità alta

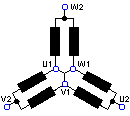
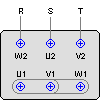
velocità bassa

Sistemi di protezione

Per proteggere l'avvolgimento di un motore trifase a induzione contro le sovratemperature causate da sovraccarichi, funzionamento senza una fase, rotore bloccato ecc..., è possibile adottare uno dei seguenti sistemi:

Colori dei Pulsanti e loro significato (CEI 44-5)

Segni grafici per i Pulsanti (CEI 44-5)

Colori degli Indicatori Luminosi e loro significato (CEI 44-5)

INTRODUZIONE

Gli effetti del passaggio della corrente elettrica nel corpo umano sono derivati da un ampio studio basato su osservazioni cliniche, ricerche bibliografiche ed esperimenti effettuati su animali, persone defunte e, in qualche caso, con correnti di breve durata, su persone vive consenzienti. In particolare sono stati studiati gli effetti sul corpo umano dell'intensità della corrente elettrica anche in funzione della sua durata, del suo percorso all'interno del corpo, delle caratteristiche elettriche dei tessuti interessati al passaggio della corrente e della forma dell'onda. In queste note si farà riferimento esclusivamente ai rischi che possono derivare dall'uso di macchine ed impianti elettrici sui posti di lavoro tenuto conto delle caratteristiche dell'energia elettrica usata in Italia.

EFFETTI SULLA SALUTE

Il comportamento del corpo umano al passaggio della corrente elettrica

I movimenti muscolari del corpo sono originati da impulsi elettrici generati dal cervello. I muscoli, stimolati da questi impulsi, reagiscono contraendosi; al di là di una visione meccanicistica del corpo, tutta la possibilità di movimento dell'uomo è correlata con la capacità fine che hanno i muscoli di reagire agli stimoli provenienti dal cervello.

Le fasce muscolari, quando vengono interessate da correnti che hanno origine da sorgenti esterne al corpo, ad esempio quando si prende la "scossa", si contraggono obbedendo anche ad esse; se la corrente "esterna" è più intensa di quella "interna" possono ingenerarsi situazioni di pericolo e le conseguenze, sul corpo umano, possono essere le più varie. Di seguito si riportano solo i fenomeni più importanti.

La contrazione muscolare

E' quel fenomeno per cui i muscoli, se attraversati dalla corrente, si irrigidiscono. In sintesi si può dire che quando le correnti sono di modesta intensità i muscoli maggiormente interessati alla contrazione sono quelli posti in prossimità del punto di ingresso della corrente. Se l'ingresso della corrente elettrica avviene attraverso una mano, come normalmente succede, la contrattura dei muscoli fa stringere la mano sull'elemento in tensione (tetanizzazione). L'infortunato, pur nella consapevolezza del rischio corso, non riesce a fare nulla per distaccarsi dalla parte in tensione. Quando si è investiti da correnti elevate, invece, tutti i muscoli, normalmente anche quelli più lontani, vengono interessati al fenomeno; fra questi anche quelli delle fasce lombari e delle cosce (eccitazione motoria). La contrazione dei muscoli degli arti inferiori comporta violenti movimenti involontari che possono causare salti dell'infortunato con caduta lontano dal punto di contatto.

L'arresto respiratorio

L' arresto viene provocato dall'entrata in contrazione dei muscoli respiratori (diaframmatici, intercostali, pettorali) con conseguente paralisi della gabbia toracica ed impedimento dei normali movimenti respiratori. In questi casi si presentano fenomeni di asfissia con progressivo impoverimento dell'ossigeno presente nei polmoni e comparsa di cianosi. Le conseguenze possono arrivare fino alla perdita di coscienza e, nei casi, più gravi alla morte dell'infortunato.

L'arresto cardiaco

Per comprendere il fenomeno occorre ricordare che il muscolo cardiaco si contrae ritmicamente sostenendo, in tal maniera, la circolazione del sangue nel corpo; banalizzando il discorso si può dire che il cuore si comporta come se fosse un motore. A differenza degli altri muscoli che vengono stimolati dalla attività elettrica del cervello, la contrazione dei muscoli cardiaci è provocata dal cuore stesso. Quando per un motivo qualsiasi si guasta e non è più in grado di elaborare gli stimoli elettrici necessari, il cuore si ferma e la circolazione del sangue nel corpo si arresta con tutte le gravi conseguenze che ne derivano. Si comprende facilmente come un passaggio di una corrente elettrica esterna, andando a sovrapporsi alla attività elettrica propria del cuore, getti le fasce muscolari cardiache in uno stato di confusione impedendo loro di svolgere la propria funzione.

Le ustioni

Alla stregua di qualsiasi circuito elettrico anche il corpo umano quando viene attraversato dalla corrente si riscalda; se la quantità di calore sviluppata è molto alta possono aversi bruciature nei tessuti attraversati dalla corrente. E' il famoso effetto Joule. La quantità di calore sviluppato è direttamente proporzionale all'intensità di corrente che attraversa il corpo, alla sua resistenza ed alla durata del fenomeno. La parte del corpo umano maggiormente interessato a questo fenomeno è la pelle. Ma quando le intensità di corrente sono molto alte si possono verificare ustioni profonde in molti tessuti e possono essere danneggiati interi arti (braccia, spalle, arti inferiori, ecc.).

Le ustioni possono essere causate anche da archi provocati da scariche elettriche prodotte da apparecchiature sotto tensione. Particolarmente pericolosi sono gli archi provenienti da apparecchiature elettriche alimentate in alta tensione.

I PRINCIPI DELLA PREVENZIONE

I rischi connessi con l'uso dell'energia elettrica sono essenzialmente:

rischi dovuti a contatti elettrici diretti (sono quelli derivati da contatti con elementi normalmente in tensione ad esempio l'alveolo di una presa, un conduttore nudo, ecc);

• rischi dovuti a contatti elettrici indiretti (sono quelli derivati da contatti che avvengono con elementi finiti sotto tensione a causa del guasto (ad esempio la scossa presa quando si apre un frigorifero o si tocca un tornio o una qualsiasi altra macchina);
• rischi di incendio dovuti a cortocircuiti o sovracorrenti;
• rischi di esplosione (sono quelli dovuti al funzionamento degli impianti elettrici installati in ambienti particolari nei quali è possibile la presenza di miscele esplosive come ad esempio nelle raffinerie, industrie chimiche, in talune centrali termiche funzionanti a gas, nei mulini, ecc).

Tutti questi rischi sono stati studiati e la prevenzione degli infortuni in questi casi si basa sull'uso di macchine ed impianti realizzati a regola d'arte, su una loro adeguata manutenzione e su un loro uso corretto.

Gli impianti e le macchine

Per legge le norme CEI forniscono una presunzione assoluta, anche se non esclusiva, di regola d'arte e quindi le apparecchiature e gli impianti realizzati e mantenuti secondo le indicazioni delle norme CEI sono da considerare sicuri. Gli impianti, inoltre, devono essere realizzati secondo i principi individuati dalla legge 46/90; in particolare devono essere:

realizzati da ditte iscritte nell'apposito albo delle imprese artigiane o nel registro delle ditte presso le Camere di Commercio;

• progettati a partire dai limiti previsti dalla legislazione vigente;
• realizzati secondo le norme CEI o normativa equivalente;
• realizzati con materiali anch'essi realizzati a regola d'arte;
• verificati ai fini della sicurezza e funzionalità;
• forniti di dichiarazione di conformità rilasciata dall'installatore completa di tutti gli allegati obbligatori.

Per quanto riguarda le macchine o i componenti elettrici non è ammesso l'uso apparecchiature "anonime" per le quali non sia possibile risalire al costruttore. In particolare ogni componente elettrico deve essere fornito degli elementi che lo identificano compiutamente (targa del costruttore, contrassegni, marcature o marchi, libretti di manutenzione ed uso, ecc.).

La manutenzione

Al fine di evitare rischi connessi con l'uso di apparecchiature rotte o deteriorate occorre controllare periodicamente lo stato di conservazione delle attrezzature che si usano segnalando al servizio di manutenzione la loro sostituzione o riparazione. L'uso di componenti elettrici deteriorati (cavi spellati, custodie rotte, connessioni elettriche approssimate, prese a spina spaccate, ecc.) fa aumentare considerevolmente il rischio di contatti elettrici.

Usi impropri

Particolare cura deve essere posta nell'uso proprio di apparecchiature elettriche. Un impianto o un apparecchio elettrico anche ben costruiti possono diventare pericolosi se utilizzati o conservati in maniera impropria. Valgono le seguenti avvertenze:

non effettuare mai riparazioni sugli impianti elettrici o sulle macchine se non si è in possesso delle caratteristiche di professionalità previste dalla legislazione vigente. Un impianto elettrico o una apparecchiatura nati sicuri possono, per errata riparazione, diventare pericolosi. Inoltre la manomissione di un impianto o di un componente fa perdere agli stessi la garanzia del costruttore;

• non utilizzare componenti non conformi alle norme. Tutta la sicurezza di un impianto finisce quando si usano utilizzatori elettrici (ad esempio spine, adattatori, prese multiple, prolunghe, lampade portatili, ecc) non rispondenti alle norme;
• non utilizzare componenti elettrici o macchine per scopi non previsti dal costruttore. In questi casi l'uso improprio del componente può ingenerare situazioni di rischio, elettrico o meccanico, non previsti all'atto della sua costruzione;
• non usare apparecchiature elettriche in condizioni di rischio elettrico accresciuto (ad esempio con le mani bagnate, con i piedi immersi nell'acqua o in ambienti umidi). In questi casi possono diventare pericolose anche tensioni abitualmente non pericolose;
• non lasciare apparecchiature elettriche (cavi, prolunghe, trapani, ecc.) abbandonate sulle vie di transito. In questi casi, oltre ad essere occasione di inciampo e di caduta di persone, i componenti sono soggetti a deterioramento meccanico non previsto dal costruttore con conseguenti situazioni di rischio.

NORMATIVA

Le più importanti leggi da rispettare nella prevenzione degli infortuni di origine elettrica sono le seguenti:

DPR 27 aprile 1955 n. 547 "Norme generali per la prevenzione degli infortuni sul lavoro";

• legge 1 marzo 1968 n. 186 "Disposizioni concernenti la produzione di materiali, apparecchiature, macchinari, installazioni ed impianti elettrici ed elettronici";
• legge 18 ottobre 1977 n. 791 "Attuazione della direttiva del Consiglio delle comunità europee (n. 73/23 CEE) relativa alle garanzie di sicurezza che deve possedere il materiale elettrico destinato ad essere utilizzato entro alcuni limiti di tensione";
• legge 5 marzo 1990 n. 46 "Norme per la sicurezza degli impianti";
• decreto legislativo 4 dicembre 1992 n. 476 "Attuazione della direttiva 89/336 CEE del Consiglio del 3 maggio 1989, in materia di ravvicinamento delle legislazioni degli stati membri relative alla compatibilità elettromagnetica, modificata dalla direttiva 93/31 CEE del Consiglio del 29 aprile 1992".

Gas: delibera 40/04 e nuovi documenti

A partire dal 1 ottobre 2004, è entrato in vigore il Titolo II della delibera riguardante gli impianti di utenza di nuova realizzazione. Da questa data sono cambiate le procedure per la compilazione della documentazione che gli installatori devono rilasciare al cliente, affinché questo possa ottenere la fornitura dall'azienda del gas.

Le procedure imposte dalla delibera, coinvolgono anche i clienti, i quali per richiedere la fornitura, devono compilare alcuni dei modelli allegati alla stessa.

Nell'esposizione dell'argomento, vedremo come e quando l'installatore ed il comune cittadino, dovranno compilare i diversi allegati alla Delibera, così come vedremo i tempi, in cui la documentazione deve essere consegnata dall'installatore al cliente e dal cliente all'azienda del gas.

In particolare, vedremo come l'installatore, deve compilare i documenti di sua competenza.

Nell'articolo, ci limiteremo a considerare degli esempi di accertamento eseguiti su impianti di nuova costruzione distinguendo tra i casi di impianti soggetti e non alla legge 46/90, ed ancora vedremo quali documenti dovranno essere presentati se una azienda sceglie la procedura di accertamento  "semplificata" o quella "completa" contemplate dalla Delibera.

Il rischio di folgorazione

Con il termine folgorazione si intende l'insieme degli effetti (dannosi) che il passaggio di una corrente elettrica può  provocare sull'organismo umano.

Appare curioso notare che tutto nacque quasi per caso allorché Galvani osservò il contrarsi dei muscoli di una rana morta posta in contatto con un bimetallo (si era circa nel 1790).

A dire il vero, l'interpretazione iniziale data dal grande studioso fu del tutto errata dato che egli ipotizzò che la contrazione fosse dovuta ad "elettricità animale che si scarica attraverso il conduttore bimetallico". Fu Alessandro Volta a fornire, qualche tempo dopo, la corretta spiegazione dei fatti.

Egli asserì che la rana costituiva un conduttore elettrolitico in grado di chiudere il circuito tra due metalli di natura diversa.

Oggi quasi tutti guardano a tale interpretazione come a quella che diede origine alla pila.

Tuttavia dal punto di vista del comportamento della rana, la stessa interpretazione portò parallelamente anche alla nascita di una importante scienza oggi nota come elettrofisiologia, cioè studio dei rapporti intercorrenti tra corrente elettrica ed organismo umano.

Era stato infatti per la prima volta osservato che il tessuto muscolare è in grado di condurre corrente elettrica.

MISURA DELLA TENSIONE

In onore del fisico italiano Alessandro Volta, è stata assunta, come unità di misura della tensione il "volt", in forma abbreviata "V". Ma di esso sono pure noti valori multipli e sottomultipli, tra i quali i più comuni sono:

Kilovolt = mille volt (simbolo: KV)

Millivolt = un millesimo di volt (simbolo: mV)

Microvolt = un milionesimo di volt (simbolo: uV)

La tensione elettrica si misura tramite uno strumento che prende il nome di "voltmetro", che viene usato principalmente da elettrotecnici ed elettricisti, mentre gli elettronici si servono di uno strumento che prende il nome di "tester", il quale è un analizzatore universale, in grado di rilevare valori di alcune grandezze fisiche, oltre che quella della tensione. Per esempio, la misura della corrente, quella dei valori capacitivi dei condensatori, delle resistenze elettriche ed altre ancora.

IL tester è dotato di due puntali, che vanno applicati sui punti circuitali in cui si presume sia presente una differenza di potenziale, oppure là dove si vuol rilevare un preciso valore di tensione. Una manopola di comando consente di commutare lo strumento sulla funzione desiderata, che può essere quella della misura della tensione continua (DCV), della tensione alternata (ACV), della corrente continua (DCmA) o della resistenza (OHM). Ma tali notizie sono superflue per chi acquista l'apparecchio, perché ogni esemplare è corredato di apposito manuale recante tutte le istruzioni per l'uso corretto dello strumento

Un esempio pratico di applicazione del tester nella misura della tensione continua, erogata da due pile piatte collegate in serie, viene offerto dalla figura 3, nella quale si può notare come il puntale nero, che fa capo all'estremità opposta con la boccola negativa del tester, sia applicato al polo negativo libero della batteria di pile, mentre quello rosso fa contatto con uno dei terminali attivi dell'interruttore chiuso. Questo puntale poteva essere applicato al morsetto positivo libero della batteria con il medesimo risultato. Si è preferito il riferimento con l'interruttore soltanto per motivi di chiarezza di disegno. Con finalità orientative nel vasto mondo delle tensioni elettriche, riportiamo alcuni valori emblematici:

cellula solare: 0,5 V

pila normale: 1,5 V

batteria d'auto: 12 V

batteria di camion: 24 V

A queste grandezze tipiche delle tensioni continue si possono aggiungere quelle delle tensioni alternate, peraltro non ancora prese in considerazione in questo corso di elettronica. Esse sono:

rete-luce domestica: 220 V

forza motrice: 380 V

rete ENEL (media): 15.000 V

rete ENEL (elevata): 200.000 V

La tensione sviluppata da un fulmine può raggiungere l'ordine di grandezza di alcuni milioni di volt.

ENERGIA ELETTRICA

Sui due poli della pila sono condensate le cariche elettriche positive, da una parte e quelle negative dall'altra. Queste cariche tendono ad attrarsi perché possiedono una certa energia potenziale, ossia una particolare attitudine a compiere del lavoro elettrico. Altrettanto accade quando si fa riferimento ad un individuo col dire che è un uomo molto energico, soltanto per segnalare la sua disposizione a lavorare intensamente. Pertanto, con le espressioni "tensione elettrica" o "differenza di potenziale" tra i due poli di una pila o, più in generale, di un generatore elettrico, si intende designare l'energia che è disponibile allo stato potenziale nelle cariche elettriche che si trovano dislocate sui due morsetti. La tensione elettrica rappresenta una grandezza fisica fondamentale nello studio di tutta l'elettronica, la cui conoscenza è agevolata da quella della struttura dell'atomo. Quando in un atomo vengono a mancare uno 0 più elettroni, questo si arricchisce di una forza di attrazione nei confronti degli elettroni stessi allo stato libero. Tale forza interpreta, a partire dallo stato infimo della materia, il concetto di tensione elettrica, perché tra atomo ed elettroni si crea una vera e propria forza di tensione, che si annulla soltanto quando gli elettroni vengono captati e ricondotti nelle orbite atomiche. L'atomo, impoverito di uno o più elettroni, diviene una carica elettrica positiva; quando invece in esso vengono introdotti altri elettroni, l'atomo diventa una carica elettrica negativa. E in presenza delle forze di attrazione, che si manifestano tra le cariche, si crea una tensione elettrica. Le cariche elettriche dello stesso nome si respingono, mentre quelle di nome diverso si attraggono. E in virtù di queste forze di attrazione e repulsione, prende avvio la corrente elettrica.

TENSIONE ELETTRICA

La tensione elettrica, cioè la forza di attrazione o repulsione che si esercita tra le cariche elettriche, prende pure i nomi di "forza elettromotrice" e "differenza di potenziale". Molti operai elettricisti la chiamano più semplicemente "la forza". In pratica, dunque, la tensione elettrica è quella forza che, appena può, mette in movimento gli elettroni, ossia genera la corrente elettrica. In tutti i fenomeni elettrici, quindi, la tensione rappresenta la causa, mentre la corrente ne costituisce l'effetto. Quando con due dita si toccano i conduttori di rete, si offre l'opportunità alla tensione elettrica di mettere in movimento gli elettroni, ovvero di dar luogo al fenomeno della corrente elettrica che, attraversando le dita della mano, provoca quella sgradevole sensazione che viene comunemente chiamata "scossa elettrica". Se vogliamo offrire un'immagine analogica di quanto appena detto, vale a dire della tensione e della corrente, possiamo far riferimento alla figura 1, nella quale è presentato un paragone idraulico. In tal caso, l'energia elettrica equivale all'energia idrica, che è una forma di energia meccanica. La pressione dell'acqua si identifica con la tensione elettrica, la portata con la corrente. 

CORRENTE ELETTRICA

È stato detto che la corrente elettrica costituisce l'effetto della tensione elettrica, che ne è la causa. Essa è rappresentata da un movimento, più o meno intenso, più o meno ordinato, di elettroni. Un movimento che può verificarsi attraverso i corpi conduttori, quelli poco conduttori ed anche nel vuoto. Un esempio di quest'ultimo tipo di corrente elettrica poteva essere ampiamente offerto dalle valvole termoioniche che, un tempo, facevano funzionare gli apparecchi radio. In ogni caso, il movimento degli elettroni, ossia la corrente elettrica, viene sollecitata da un generatore di tensione o, meglio, di energia elettrica. Fin d'ora possiamo anticipare una notizia relativa alla corrente elettrica, ricordando che, quando gli elettroni si muovono tutti in uno stesso verso, in modo uniforme, essi rappresentano la corrente continua. Quando invece il moto elettronico è disordinato e variabile, la corrente è pur essa variabile. Attraverso i fili conduttori installati nelle nostre case, quelli che fanno accendere le lampadine per l'illuminazione e fanno funzionare gli elettrodomestici, corrono gli elettroni, cioè le cariche elettriche elementari, movendosi in entrambi i sensi, in avanti e all'indietro, dando luogo a quel tipo particolare di corrente elettrica che prende il nome di corrente alternata.

MISURA DELLA CORRENTE

L'intensità di corrente, ossia il numero di elettroni che attraversano la sezione di un conduttore elettrico in un minuto secondo, costituisce una grandezza fisica la cui unità di misura è 1'ampère, in modo abbreviato indicata con la lettera A. I filamenti delle comuni lampadine ad incandescenza sono percorsi da correnti elettriche alternate la cui intensità può variare da alcuni decimi di ampère sino ad alcuni ampère. I motori elettrici delle vetture tramviarie possono assorbire una corrente di valore compreso fra i 50 e i 100 ampère. L'ampère è un'unità di misura della corrente poco usata in elettronica, dove si ha a che fare, quasi sempre, con correnti la cui intensità è inferiore all'ampère. Si fa dunque uso di valori che sono sottomultipli dell'ampère. Essi sono:

Milliampère = un millesimo di ampère (simbolo: mA)

Microampère: un milionesimo di ampère (simbolo: uA)

Lo strumento elettrico atto a rilevare le misure dell'intensità di corrente prende il nome di amperometro, ma questo viene principalmente usato nel settore elettrotecnico per la misura di correnti particolarmente intense. Per la misura di correnti più deboli si usa il milliamperometro ed il microamperometro. In elettronica si fa uso del tester.

I PERICOLI DELLA CORRENTE

I circuiti elettronici, qualche volta, possono essere fonte di pericolose scosse elettriche. È necessario quindi essere preparati teoricamente su tale argomento, in modo da poter agire con la massima disinvoltura e sapere quando è possibile distrarsi e quando invece si deve conservare la massima attenzione onde evitare spiacevoli inconvenienti.
Contrariamente a quanto si può credere, non sono le tensioni elevate le cause prime di conseguenze fisiologiche anche gravi, mentre le colpe debbono attribuirsi sempre alle correnti che attraversano parzialmente o totalmente il corpo umano. Il quale accusa già la scossa elettrica quando è attraversato da una corrente inferiore al milliampere. A1 contrario, l'effetto della tensione è nullo se il contatto avviene in modo che sia nulla la corrente che attraversa l'organismo. Facciamo un esempio. Sulla bobina ad alta tensione, dell'impianto elettrico dell'autovettura, è presente un voltaggio dell'ordine di alcune migliaia di volt. Ma questa, se applicata al corpo umano, non costituisce alcun pericolo mortale, perché la corrente che da essa si può assorbire è di debole intensità. Se le tensioni rappresentano un pericolo per l'incolumità fisica, ciò deriva dal fatto che i valori elevati di queste hanno maggiori possibilità di mettere in movimento una grande quantità di elettroni, cioè di avviare correnti elettriche molto intense..

Principali grandezze elettriche

Carica elettrica : è la quantità di elettricità positiva o negativa di un corpo, essa è sempre un multiplo intero della carica elementare (quanto elementare pari alla carica di un elettrone). L'unità di misura della quantità di carica elettrica è il coulomb. 1 [C] è, a meno del segno, la carica posseduta da 6,242·10¹⁸ elettroni. Nello studio delle reti che noi faremo, trascureremo la natura corpuscolare della carica elettrica ed immagineremo che tale grandezza fisica vari con continuità.

Intensità di corrente : è il rapporto tra la quantità di carica elettrica che attraversa la sezione di un conduttore ed il tempo impiegato per tale attraversamento. Se il tempo impiegato ha valore finito si parla di intensità media:

[A]

se il tempo impiegato ha valore infinitesimo si parla di intensità istantanea:

[A]

Si dice che l'intensità di corrente vale 1 [A] se nel tempo di 1 [s] la sezione del conduttore è attraversata da 1 [C] di carica elettrica.

Per convenzione, si assume quale verso di riferimento della corrente quello relativo al movimento di carica positiva, anche se nella maggior parte dei conduttori le cariche libere il cui flusso costituisce corrente sono elettroni (cariche negative).

Corrente impressa : è l'intensità di corrente che un generatore ideale di corrente imprime nel ramo ove esso si trova inserito.

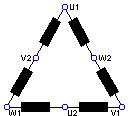
Differenza di potenziale (tensione elettrica) : si intende sempre valutata tra due punti, ad esempio A e B , si indica con V_AB [V] ed è espressa dal rapporto tra il lavoro W [J] necessario per trasferire la carica positiva Q [C] dal punto A al punto B e la carica stessa:

[V]

Si considera positiva se, nel passare da A a B, la carica positiva compie lavoro cedendo all'esterno parte della propria energia potenziale elettrica che si trasformerà in altra forma, si considera negativa se è dall'esterno che si deve compiere lavoro aumentando così l'energia potenziale elettrica della carica. L'unità di misura della differenza di potenziale è il volt. Si dice che tra due punti vi è la d.d.p. di 1 [V] se lo spostamento di 1 [C] di carica tra essi comporta un lavoro di 1 [Joule].

Potenziale : si intende sempre valutato in un punto, ad esempio A , si indica con V_A [V], e rappresenta la d.d.p. tra il punto considerato ed un punto di riferimento ( chiamato punto di massa ) al quale si assegna il valore nullo di potenziale. Il potenziale è legato alla differenza di potenziale dalla seguente relazione V_AB = V_A - V_B [V].

Caduta di tensione : è la d.d.p. valutata ai capi di un utilizzatore o di un generico dispositivo passivo. Rappresenta il lavoro compiuto da un coulomb di carica elettrica che attraversi l'utilizzatore.

Forza elettromotrice : è la d.d.p. che un generatore ideale di tensione impone tra i due punti attraverso i quali esso è inserito nella rete. Rappresenta l'energia potenziale elettrica posseduta da un coulomb di carica elettrica separata e raccolta sui poli del generatore.

Potenza elettrica : è, in un certo istante t e con riferimento ad un bipolo di morsetti A e B , il prodotto tra i valori istantanei della corrente i(t) entrante nel morsetto A del bipolo e della tensione v_AB(t) presente tra i capi A e B del bipolo:

Infatti al passaggio da A a B della quantità di carica dq [C] corrisponde un lavoro pari a:

Se tale passaggio avviene nel tempo dt [s] la potenza associata al lavoro vale:

Se il risultato del prodotto è positivo si ha che nel bipolo avviene una trasformazione da energia elettrica in altra forma, se il risultato è negativo avviene la trasformazione inversa.

Leggi e principi fondamentali

Legge di Ohm per i conduttori filiformi

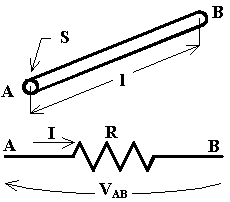
La resistenza elettrica R [] di un conduttore metallico filiforme dipende dalla natura del conduttore e dalle sue dimensioni secondo la relazione:

R = ( · l) / S

con  in [·mm²/m] , l in [m] , S in [mm²] , si ricorda che la resistività elettrica  dipende dalla temperatura.

La caduta di tensione ai capi di un utilizzatore dipende dalla resistenza dell'utilizzatore ed è direttamente proporzionale alla corrente che lo attraversa ( legge di Ohm ):

V_AB = R · I [V] , V_BA = - V_AB = -R · I [V]

la corrente percorrendo l'utilizzatore determina la riduzione dell'energia potenziale posseduta dalla carica elettrica il cui flusso costituisce la corrente stessa, tale energia potenziale elettrica si trasforma in calore (o lavoro meccanico, o lavoro chimico secondo il tipo di utilizzatore) e viene così ceduta all'esterno del sistema "rete elettrica". Da tale fatto dipende la relazione tra il verso della corrente ed il verso della caduta di tensione ai capi dell'utilizzatore, i due versi sono ovviamente opposti.

Variazione della resistività elettrica con la temperatura

Se t [·mm²/m] e t [°C^-1] sono la resistività elettrica ed il coefficiente di temperatura di un determinato conduttore alla temperatura t [°C] , la resistività elettrica alla temperatura T varrà:

_T = t·(1 + t·(T-t)) [·mm²/m]

Inoltre vale la relazione:

con H = 234,5 [°C] per il rame ed H = 230 [°C] per l'alluminio. T , t , R_T , R_t sono due diverse temperature e le rispettive resistenze.

Legge di Ohm generalizzata applicata ad un circuito chiuso

Dato un circuito elettrico, tutto serie, composto di un'unica maglia e quindi interessato da un'unica corrente, la somma algebrica delle f.e.m. dei generatori presenti è uguale alla somma aritmetica delle c.d.t. nei vari utilizzatori :

dove le f.e.m. vanno prese positive se concordi col verso della corrente.

Vediamo un esempio riferito ad un circuito in corrente continua :

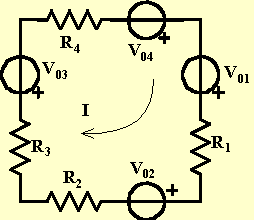
+V₀₁ -V₀₂ -V₀₃ +V₀₄ = R₁·I + R₂·I + R₃·I + R₄·I = I·( R₁+ R₂+ R₃+ R₄ )

Legge di Ohm generalizzata applicata ad un tronco di circuito

La d.d.p. ai capi di un tronco di circuito, anche costituito da più rami, è pari alla somma algebrica delle f.e.m. dei generatori e delle c.d.t. negli utilizzatori presenti lungo il tronco :

Le une e le altre devono essere prese positive se contribuiscono a rendere positiva l'estremità del tronco ( A ) assunta a potenziale maggiore.

Per quanto riguarda la c.d.t. negli utilizzatori, è bene ricordare che essa presenta la polarità positiva nel morsetto ove entra la corrente, negativa ove la corrente esce.

Vediamo un esempio riferito ad un circuito in corrente continua :

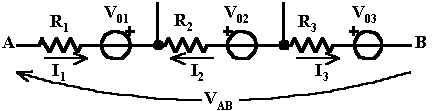
Se decidiamo di determinare V_AB , significa che supponiamo V_A > V_B e quindi scriveremo:

V_AB = -V₀₁ + V₀₂ + V₀₃ + R₁·I₁ - R₂·I₂ + R₃·I₃ [V]

Primo principio di Kirchhoff

La somma delle correnti entranti in un nodo è uguale alla somma delle correnti uscenti dal nodo :

Il principio è valido pure per un nodo esteso, dove con nodo esteso si intende una porzione di rete elettrica delimitata da una sezione chiusa della rete medesima.

Vediamo un esempio riferito ad un circuito in corrente continua :

I₁ + I₄ = I₂ + I₃ + I₅

Secondo principio di Kirchhoff

La somma algebrica di tutte le d.d.p. (f.e.m. e c.d.t.) che si incontrano percorrendo una qualsiasi maglia chiusa di una rete elettrica è pari a zero. Tale fatto risulta ovvio, infatti il punto di partenza coincide col punto di arrivo e, quindi, non vi può essere variazione di potenziale elettrico :

Per applicare tale legge conviene scegliere innanzitutto un verso positivo ( + ) di percorrenza della maglia e confrontare le varie d.d.p. con tale verso al fine di stabilire se i singoli contributi sono da considerarsi positivi o negativi (è bene tenere conto del fatto che le c.d.t. sulle resistenze hanno verso opposto alle correnti che le producono).

Vediamo un esempio riferito ad un circuito in corrente continua :

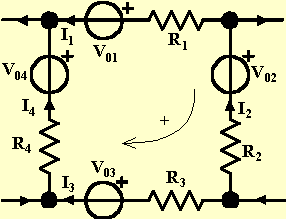
+ V₀₁ + R₁·I₁ - V₀₂ + R₂·I₂ - V₀₃ - R₃·I₃ + V₀₄ - R₄·I₄ = 0

Riduzione di resistenze in serie o parallelo

Più resistenze si dicono in serie quando sono percorse dalla stessa corrente, in tal caso la resistenza equivalente vale:

R_S = R₁ + R₂ + R₃ + ...

Più resistenze si dicono in parallelo quando ai loro capi presentano la stessa tensione, in tal caso la resistenza equivalente vale:

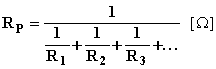
Trasformazione triangolo - stella e viceversa

Con riferimento ad un circuito in corrente continua :

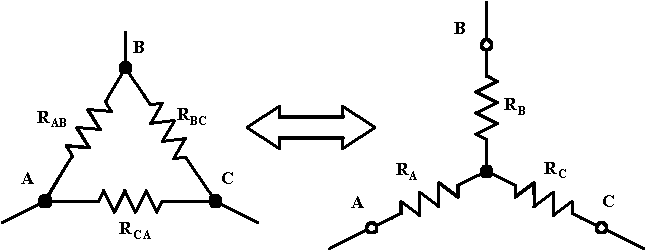
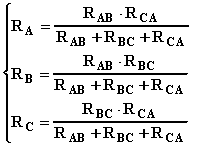
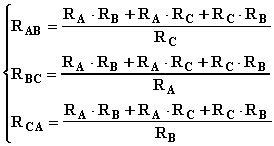
Trasformazione di generatori reali

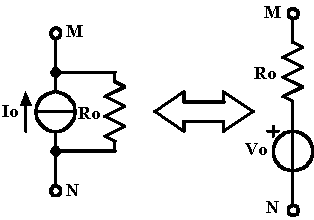
I modelli di generatore elettrico si dicono reali se tengono conto delle dissipazioni di potenza e delle cadute di tensione che si hanno internamente ai generatori stessi, in tal caso il circuito equivalente presenta il parametro resistenza interna Ro. Con riferimento ai generatori reali di tensione e corrente continua si ha:

Osservazione : se in una rete elettrica è presente un generatore ideale di tensione, allora è nota la d.d.p. tra i due punti ai quali è applicato il generatore e tale d.d.p. è pari alla f.e.m. del generatore ideale di tensione. Se in una rete elettrica è presente un generatore ideale di corrente, allora è nota la corrente nel ramo in serie al quale è inserito il generatore e tale corrente è pari alla corrente impressa del generatore ideale di corrente.

Legge di Joule

Quando una resistenza elettrica è attraversata da una corrente accade che parte dell'energia elettrica potenziale posseduta dalla carica elettrica (il cui flusso costituisce la corrente stessa) si trasforma in calore (infatti il potenziale elettrico diminuisce mano a mano che la corrente attraversa la resistenza). La quantità di calore sviluppato si calcola moltiplicando la potenza elettrica per il tempo. Con riferimento ad un circuito in corrente continua (ma la cosa è analoga in corrente alternata) si ha:

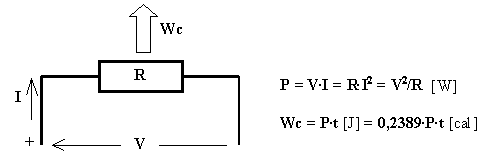
Additività delle potenze elettriche

In una rete elettrica qualsiasi (purché non interconnessa con altre reti), la somma delle potenze generate dai generatori elettrici (calcolate come prodotto della f.e.m. per la corrente erogata) è sempre uguale alla somma delle potenze dissipate per effetto Joule nelle resistenze elettriche presenti nella rete.

Resistività e coefficienti di temperatura dei materiali più comuni: tabella

La tabella sottostante riporta la resistività elettrica ed il coefficiente di temperatura di alcuni materiali riferiti alla temperatura di 0 [°C]

Se servono la resistività ed il coefficiente di temperatura ad una temperatura t [°C] diversa da 0 [°C], si possono calcolare con le seguenti espressioni:

Risoluzione mediante i principi di Kirchhoff

In una rete elettrica, indicando con n il numero dei nodi, con m il numero delle maglie indipendenti e con r il numero dei rami, si ha sempre (r = n - 1 + m) . La risoluzione mediante i principi di Kirchhoff consiste nello scrivere un sistema di r equazioni in r incognite (le correnti nei rami). Le prime (n -1) equazioni consistono nel primo principio di Kirchhoff applicato ad (n -1) nodi, le rimanenti (r - n + 1) equazioni consistono nel secondo principio di Kirchhoff applicato a (r - n + 1) maglie indipendenti. Più maglie si dicono indipendenti se nessuna di loro è una combinazione lineare delle altre, ad esempio tutte le maglie topologicamente contigue e che non si comprendono l'una nell'altra sono sicuramente indipendenti.

Con riferimento alla rete in corrente continua riportata nella figura sottostante, si individuano quattro nodi, otto maglie delle quali tre sono indipendenti e sei rami. Quindi, dopo aver prefissato un arbitrario verso per la corrente in ciascuno dei sei rami e per l'orientamento di ciascuna maglia indipendente, scriveremo un sistema lineare di sei equazioni in sei incognite. Delle sei equazioni, tre saranno relative ai rami e tre alle maglie. Risolvendo il sistema si determineranno le intensità delle sei correnti. Se l'intensità è positiva si potrà dire che il verso prefissato è quello effettivo, diversamente il verso effettivo sarà opposto a quello prefissato

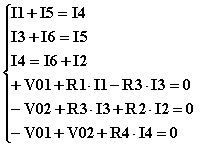
Risoluzione mediante il metodo di Maxwell

Si assumono come incognite le correnti di circolazione delle maglie indipendenti che sono correnti fittizie e non rappresentano quelle che percorrono ciascun ramo della rete. Quindi, detto m il numero delle maglie indipendenti, si ha m = r - (n-1) e di conseguenza il numero delle incognite è minore di quello del metodo precedente. Il sistema risolvente si comporrà di tante equazioni, corrispondenti al secondo principio di Kirchhoff, quante sono le maglie indipendenti. Con questo metodo il primo principio di Kirchhoff risulta senz'altro verificato in quanto la corrente in ogni nodo si intende una volta entrante ed una volta uscente. La corrente in ogni ramo comune a due maglie contigue risulta la somma algebrica delle due correnti fittizie relative alle due maglie.

Applichiamo il metodo alla rete già risolta con Kirchhoff, assumendo quali correnti fittizie di maglia Im1 (maglia superiore di sinistra), Im2 (maglia superiore di destra), Im3 (maglia inferiore). I versi delle correnti di maglia sono stati scelti arbitrariamente. Si dovrà comporre un sistema lineare di tre equazioni in tre incognite (le correnti fittizie di maglia) essendo tre il numero delle maglie indipendenti:

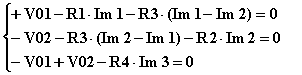
Risolvendo il sistema si determinano le tre correnti di maglia Im1 , Im2 , Im3. Per le correnti nei sei rami della rete bisogna, per prima cosa, prefissarne i versi. Supponendo che i versi siano quelli riportati nello schema elettrico, le correnti varranno:

I1 = -Im1 [A], I2 = -Im2 [A], I3 = +Im1-Im2 [A]

I4 = -Im3 [A], I5 = +Im1-Im3 [A], I6 = +Im2-Im3 [A]

Teorema del generatore equivalente di Thevenin

Risulta particolarmente adatto per determinare la corrente Ir che circola in un qualsiasi ramo (o la tensione Vr ai capi di esso) di una rete elettrica lineare comunque complessa. Considerata allora una rete elettrica lineare nella quale siano accessibili due morsetti P e Q qualsiasi, il teorema afferma che, per quanto riguarda il calcolo della corrente (o della tensione) relativa al ramo ad essi collegato, il resto della rete equivale ad un generatore reale di tensione avente f.e.m. Veq e resistenza interna Req :

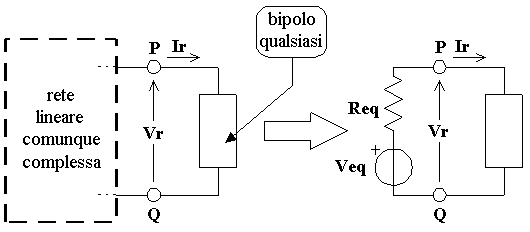
Il generatore reale di tensione Veq , Req è chiamato generatore equivalente di Thevenin e la rete semplificata è chiamata rete equivalente di Thevenin.

La f.e.m. Veq del generatore equivalente è il valore della tensione a vuoto (cioè dopo aver distaccato il ramo interessato) esistente tra i morsetti P e Q.

La resistenza Req è quella della rete di partenza, resa passiva e priva del ramo interessato, vista dai morsetti P e Q. Per rendere passiva la rete di partenza bisogna annullarne i generatori, ovvero aprire i generatori ideali di corrente e cortocircuitare quelli di tensione.

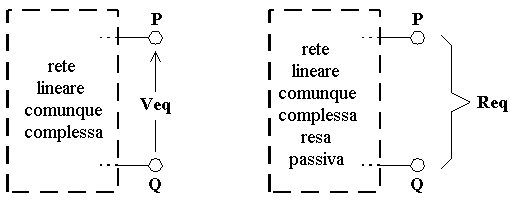
E' importante osservare che la polarità positiva del generatore equivalente di Thevenin deve essere rivolta verso lo stesso morsetto del ramo interessato rispetto al quale si è assunta positiva la d.d.p. Veq quando questa è stata calcolata.

Teorema del generatore equivalente di Norton

E' il duale di quello di Thevenin, solo che il generatore reale equivalente, anziché di tensione, è di corrente. Esso viene chiamato generatore equivalente di Norton.

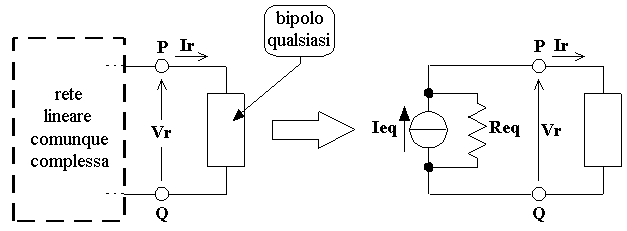
La sua resistenza interna Req si determina così come già visto per il generatore di Thevenin. La sua corrente impressa Ieq è quella corrente che, nella rete lineare di partenza, circolerebbe nel cortocircuito che unisce i punti P e Q .

E' importante osservare che il verso della corrente impressa Ieq è legato al verso col quale si è trovata la corrente nel cortocircuito che unisce i punti P e Q . Più precisamente la corrente impressa Ieq deve puntare verso P se la corrente nel cortocircuito è stata determinata col verso che va da P a Q .

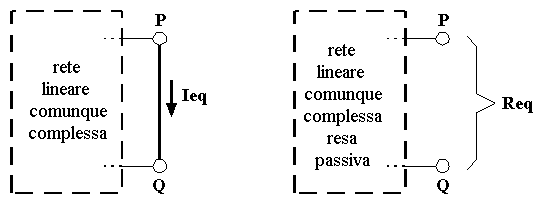
Principio di sovrapposizione degli effetti

La corrente in un ramo qualsiasi (o la d.d.p. ai capi dello stesso) appartenente ad una rete elettrica lineare comunque complessa nella quale agiscono simultaneamente più generatori di tensione e/o di corrente, si ottiene facendo la somma algebrica delle correnti (o delle d.d.p.) relative al ramo considerato e dovute a ciascun generatore supposto agente da solo, con i rimanenti annullati (cortocircuitati se di tensione, aperti se di corrente).

Principio di Millman

Si applica quando la rete ha solo due nodi M ed N , cioè è costituita da rami tutti in parallelo tra di loro. Se J è il numero di rami, Vok è la f.e.m. totale per il ramo k-esimo , Rk è la resistenza totale per il ramo k-esimo , la d.d.p. fra i due nodi vale:

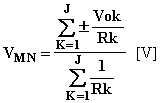
Nella somma algebrica a numeratore, il singolo termine è positivo se la f.e.m. Vok è tale da rendere positivo il potenziale del punto M rispetto al potenziale del punto N .

Caratteristica esterna e rendimento dei generatori, teorema della massima potenza trasferita

Caratteristica esterna di un generatore

I generatori elettrici sono macchine che trasformano energia di altro tipo in energia elettrica. Per ora ci limitiamo a considerare generatori di tensione e corrente continua, ma esistono (ed anzi sono molto più diffusi in ambito elettrotecnico) anche i generatori di tensione e corrente alternata. Il motivo per il quale esistono due diversi modelli, generatore di tensione e generatore di corrente, per la stessa macchina è dovuto al fatto che nelle applicazioni si hanno sia dispositivi che tendono a mantenere costante la tensione d'uscita al variare della resistenza dell'utilizzatore alimentato, e per essi è più opportuno come modello il generatore di tensione, sia dispositivi che tendono a mantenere costante la corrente erogata al variare della resistenza dell'utilizzatore alimentato, e per essi è più opportuno come modello il generatore di corrente.

Per caratteristica esterna di un generatore si intende la funzione V = f (I) ovvero la tensione d'uscita in funzione della corrente erogata.

Vediamo nel caso di generatori ideali (cioè privi di dissipazioni interne di potenza) quale è l'andamento della caratteristica esterna, allo scopo supponiamo che i generatori alimentino un utilizzatore avente una resistenza Ru che dobbiamo immaginare variabile tra [] (funzionamento a vuoto del generatore) e 0 [] (funzionamento in cortocircuito del generatore):

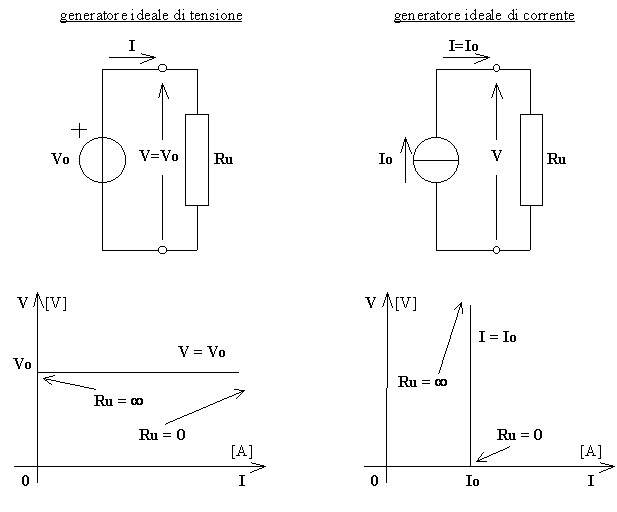
Per il generatore ideale di tensione la caratteristica esterna sarà una retta orizzontale di equazione V = Vo in quanto la sua tensione d'uscita è rigorosamente uguale alla sua forza elettromotrice, qualsiasi sia la resistenza dell'utilizzatore alimentato e quindi qualsiasi sia la corrente erogata. Per il generatore ideale di corrente la caratteristica esterna sarà una retta verticale di equazione I = Io in quanto la corrente erogata è rigorosamente uguale alla sua corrente impressa, qualsiasi sia la resistenza dell'utilizzatore alimentato e quindi qualsiasi sia la tensione d'uscita.

Passiamo ora ad esaminare il caso di generatori reali (cioè generatori per i quali si considerino i fenomeni dissipativi interni). Il circuito equivalente dei generatori dovrà ora prevedere una resistenza interna Ro grazie la quale si può tenere conto delle perdite interne di potenza. Tale resistenza verrà messa in serie nel caso del generatore di tensione (e vale zero se il generatore è ideale), mentre verrà messa in parallelo nel caso del generatore di corrente (e vale infinito se il generatore è ideale). Infatti la resistenza interna, oltre che delle perdite di potenza, dovrà pure tenere conto della diminuzione della tensione d'uscita all'aumentare della corrente erogata per il generatore reale di tensione e della diminuzione della corrente erogata all'aumentare della tensione d'uscita per il generatore reale di corrente.

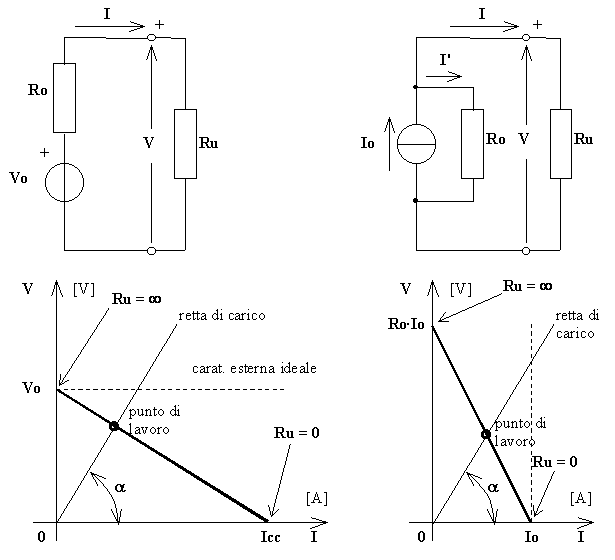
Vediamo la discussione nel caso del generatore reale di tensione, il caso del generatore reale di corrente è del tutto analogo.

L'equazione della caratteristica esterna V = f (I) si determina applicando la legge di Ohm al tronco di circuito comprendente il generatore:

V = Vo - Ro·I

si tratta dell'equazione di una retta sul piano cartesiano (I,V) avente pendenza negativa, la pendenza è tanto più accentuata quanto più è grande la resistenza interna del generatore. L'intersezione con l'ordinata rappresenta il punto di funzionamento a vuoto essendo nulla la corrente erogata, quindi con resistenza dell'utilizzatore di valore infinito, e la tensione d'uscita è in tal caso pari alla f.e.m. del generatore. L'intersezione con l'ascissa rappresenta il punto di funzionamento in cortocircuito essendo nulla la tensione d'uscita, quindi con resistenza dell'utilizzatore di valore nullo, e la corrente erogata è in tal caso uguale a:

V = 0  Icc = Vo / Ro

Per una generica condizione di funzionamento del generatore si avrà una tensione d'uscita che risulterà inferiore alla f.e.m. del generatore stesso di una quantità pari a Ro·I che rappresenta la caduta di tensione interna al generatore dovuta alla sua resistenza interna.

Viene chiamata retta di carico l'equazione corrispondente alla legge di Ohm applicata all'utilizzatore, ovvero:

V = Ru·I

Sul piano cartesiano (I,V) tale equazione rappresenta una retta passate per l'origine ed avente pendenza positiva. Se i due assi hanno il medesimo fattore di scala, risulta essere:

tg() = Ru

quindi la retta di carico coincide con l'ascissa se Ru = 0, coincide con l'ordinata se Ru = . Il punto di intersezione tra la caratteristica esterna e la retta di carico individua il punto di lavoro del sistema formato dal generatore e dall'utilizzatore, ovvero la coppia di valori (I,V) che soddisfa il sistema elettrico complessivo.

Rendimento elettrico di un generatore

Data una qualsiasi macchina si definisce rendimento  il rapporto tra la potenza erogata Pe e la potenza assorbita Pa. Siccome ogni macchina reale è inevitabilmente sede di perdite di potenza Pd, risulterà la potenza erogata sempre inferiore alla potenza assorbita e quindi il rendimento sarà sempre inferiore all'unità:

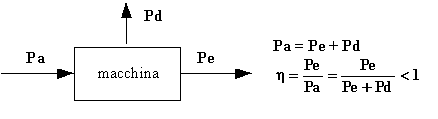
Per un generatore elettrico si definisce rendimento elettrico _E il rapporto tra la potenza elettrica erogata Pe e la potenza elettrica generata Pg:

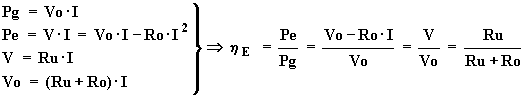
Naturalmente il termine (Ro·I²) rappresenta le perdite di potenza per effetto Joule sulla resistenza interna del generatore. Abbiamo considerato un generatore reale di tensione, per quello di corrente valgono considerazioni analoghe.

Teorema della massima potenza trasferita

Vediamo, sempre per il generatore reale di tensione, come varia la potenza erogata in funzione della resistenza dell'utilizzatore. Allo scopo è necessario studiare la funzione Pe = f(Ru):

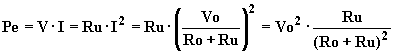
Si osserva che per Ru = 0 risulta essere Pe = 0, inoltre per Ru tendente ad infinito di nuovo Pe tende a zero, infine Pe assume valori sempre positivi. Quindi la funzione Pe = f(Ru) ha un andamento a campana e si potrebbe dimostrare che il massimo della campana si ha quando Ru è uguale a Ro:

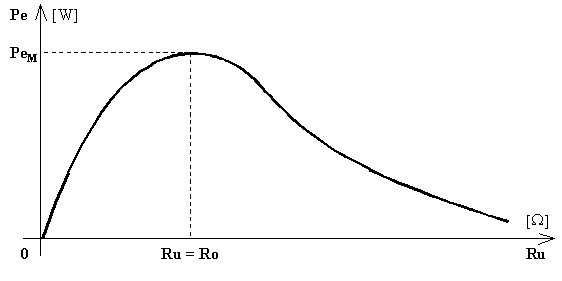
Ponendo nell'equazione Pe = f(Ru) al posto di Ru la Ro si ottiene l'espressione della massima potenza erogabile dal generatore:

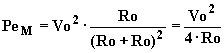
Per quanto riguarda il rendimento elettrico in coincidenza della condizione Ru = Ro di massima potenza erogata si ha:

Si può quindi enunciare il seguente teorema della massima potenza trasferita:

se una rete elettrica (o un generatore reale) alimenta un'altra rete (o un carico) si ha il massimo trasferimento di potenza quando la resistenza di uscita della rete alimentante (o la resistenza interna del generatore) è uguale alla resistenza d'ingresso della rete alimentata (o alla resistenza del carico), si suole dire allora che il carico è adattato in potenza. In queste condizioni il rendimento vale 0,5 e, quindi, il problema dell'adattamento è particolarmente sentito nei circuiti a basso livello di potenza (telefonia, telegrafia, ecc.) e non in quelli ad alto livello di potenza tipici delle applicazioni industriali dell'elettrotecnica.

Potenza elettrica associata ad una corrente in quadratura con la tensione, potenza reattiva

Questo stato di regime si verifica in un circuito puramente induttivo (corrente in ritardo di 90° sulla tensione), oppure puramente capacitivo (corrente in anticipo di 90° sulla tensione). Eseguendo per ogni istante il prodotto v(t)·i(t) si ottiene p(t) che è una grandezza ancora sinusoidale di frequenza doppia rispetto alla corrente ed alla tensione. Si osserva che l'asse di simmetria della p(t) coincide con l'asse dei tempi (ascissa) e, quindi, la potenza non ha più carattere pulsante ma ha carattere alternativo e conseguentemente il suo valor medio è nullo.

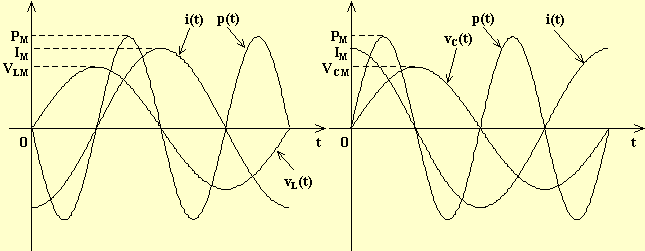
Quindi, in un circuito nel quale la tensione e la corrente sono in quadratura tra di loro, la potenza istantanea è tale per cui l'energia viene alternativamente scambiata tra il circuito ed il campo (elettrico per la capacità, elettromagnetico per l'induttanza), più precisamente l'energia viene ceduta dal circuito al campo quando la potenza è positiva e viceversa quando è negativa. Quindi, considerando un intero periodo, il bilancio energetico tra circuito e campo è nullo così che si può dire che la potenza media è nulla, ovvero non vi è alcuna trasformazione permanente di energia. Per tali motivi si suole dire che un circuito puramente induttivo o puramente capacitivo non è interessato da potenza attiva.

Viene convenzionalmente considerata, sotto il nome di potenza reattiva, la quantità . Tale potenza reattiva non riveste assolutamente il significato fisico di potenza, ma costituisce un puro riferimento convenzionale ai valori efficaci della tensione V [V] e della corrente I [A] in quadratura tra di loro e, per questa ragione, la potenza reattiva non si misura in [Watt] ma si esprime in VoltAmpereReattivi [VAR].

A tale potenza vengono convenzionalmente associati segni opposti a secondo che il circuito sia induttivo o capacitivo. Le norme assegnano il segno positivo alla potenza reattiva induttiva Q_L = X _L·I² ed il segno negativo alla potenza reattiva capacitiva Q_C = X _C·I² . Ciò perché è positivo lo sfasamento tra tensione e corrente nel circuito induttivo, negativo nel circuito capacitivo.

Impedenza elettrica, triangolo delle potenze

Si tratta di un operatore vettoriale (quindi una grandezza complessa, non una grandezza variabile sinusoidalmente nel tempo) così definito:

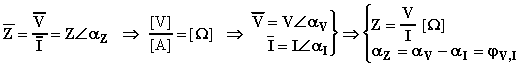
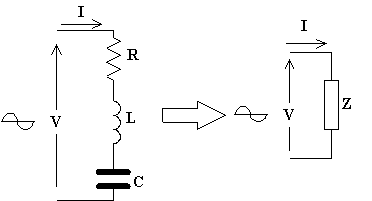
L'impedenza riassume la resistenza e la reattanza complessive di un ramo infatti se  è la pulsazione della tensione alternata sinusoidale applicata al ramo, si ha:

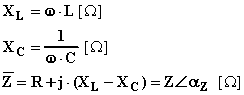
Il modulo dell'impedenza vale ovviamente:

mentre il suo argomento vale:

e tale argomento coincide con lo sfasamento tra la tensione applicata all'impedenza e la corrente che percorre l'impedenza.

Le potenze che riguardano l'impedenza sono:

potenza attiva 

P = V·I·cos(_V,I) = R·I² [W]

potenza reattiva, da considerarsi induttiva se positiva, da considerarsi capacitiva se negativa :

Q = V·I·sen(_V,I) = (X_L - X_C)·I² [VAR]

modulo potenza apparente, che riassume le prime due :

potenza apparente complessa ( è il coniugato di ) :

Le tre potenze di cui sopra si possono riassumere nel seguente triangolo delle potenze:

per il quale valgono le seguenti relazioni:

Teorema di Boucherot

In un sistema elettrico in regime sinusoidale costituito da più utilizzatori si può dire che:

a) la potenza attiva totale è data dalla somma aritmetica delle singole potenze attive:

b) la potenza reattiva totale è data dalla somma algebrica delle singole potenze reattive assunte positive se induttive, negative se capacitive:

c) la potenza apparente complessa totale è data dalla somma vettoriale delle singole potenze apparenti complesse, in ogni caso il modulo della potenza apparente totale si può più convenientemente determinare con:

Ammettenza elettrica

E' un operatore vettoriale definito come l'inverso dell'impedenza:

La parte reale dell'ammettenza è chiamata conduttanza, la parte immaginaria è chiamata suscettanza. L'ammettenza, la conduttanza e la suscettanza si misurano in siemens, [^-1] = [S].

Si dimostra facilmente che il modulo dell'ammettenza è pari all'inverso del modulo dell'impedenza, mentre l'argomento dell'ammettenza è l'opposto dell'argomento dell'impedenza.

L'operatore vettoriale ammettenza può essere usato per la risoluzione delle reti elettriche. La legge di Ohm diventa:

La serie di più ammettenze si calcola con l'espressione:

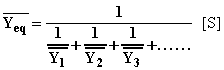
mentre il parallelo di più ammettenze si calcola con l'espressione:

Vediamo ora la trasformazione serie-parallelo dei parametri di una impedenza:

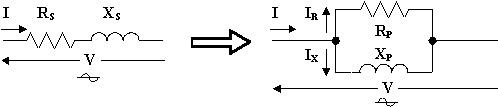
Perché i due circuiti siano equivalenti, quando vengono sottoposti alla stessa tensione devono assorbire la stessa corrente. Quindi sarà:

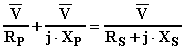
da cui:

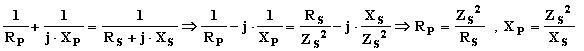
Si osserva che i parametri parallelo dell'impedenza altro non sono che l'inverso della conduttanza e della suscettanza dell'ammettenza equivalente all'impedenza data.

Risonanza

Un circuito in corrente alternata, comunque complesso, nel quale siano presenti resistenze, induttanze e capacità si dice in risonanza quando rispetto alla tensione che lo alimenta si comporta come un circuito puramente ohmico.

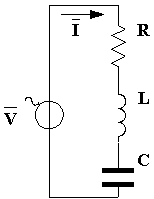
Si parla di risonanza serie (chiamata anche risonanza di tensione) quando i bipoli R , L , C sono collegati in serie tra di loro. Affinché il circuito si comporti come se fosse puramente ohmico deve ovviamente essere X_L = X_C . La pulsazione per la quale questa condizione si verifica è chiamata pulsazione di risonanza e vale:

come è facile dimostrare.

Per pulsazioni più grandi di ₀ il circuito si comporta da ohmico-induttivo, tendente al puramente induttivo per ₀ tendente ad infinito. Per pulsazioni più piccole di ₀ il circuito si comporta da ohmico-capacitivo, tendente al puramente capacitivo per ₀ tendente a zero.

Se si immagina di alimentare il circuito con un generatore di tensione di valore efficace costante e pulsazione variabile, è facile verificare che in coincidenza della pulsazione di risonanza è massima la corrente che varrà [A]. Quindi ai capi dell'induttanza e della capacità si può avere una c.d.t. molto grande, anche maggiore della tensione applicata al circuito. Infatti se per si ha X_L0 = X_C0 >> R accadrà che sarà V_L0 = V_C0 >> V_R0 = V.

Si parla di risonanza parallelo (chiamata anche risonanza di corrente o antirisonanza) quando si presenta il circuito riportato sopra. La pulsazione di risonanza, per la quale la tensione ai capi del parallelo è in fase con la corrente che lo alimenta, si dimostra che vale:

e, nel caso di R_L = R_C, tale espressione diventa uguale a quella della risonanza serie. In coincidenza di ₀ si ha che il parallelo assume il valore massimo di impedenza (tale impedenza è puramente ohmica) pari a:

Per pulsazioni più grandi di ₀ il circuito si comporta da ohmico-capacitivo, tendente al puramente capacitivo per ₀ tendente ad infinito. Per pulsazioni più piccole di ₀ il circuito si comporta da ohmico-induttivo, tendente al puramente induttivo per ₀ tendente a zero.

Se si immagina di alimentare il circuito con un generatore di corrente di valore efficace costante e pulsazione variabile, accade che in coincidenza della pulsazione di risonanza è massima la tensione ai capi del parallelo. Quindi nei rami del parallelo si può avere una corrente molto grande, anche maggiore della corrente erogata dal generatore.

La corrente elettrica Torna all'indice argomenti >
	L'effetto Joule Il motivo per cui l'energia elettrica è così utile all'uomo è che essa può facilmente essere convertita in altre forme di energia, in particolare energia termica (calore). Ciò può essere facilmente osservato in un resistore, che quando è percorso da una corrente elettrica si riscalda, ovvero libera o dissipa una parte dell'energia elettrica sotto forma di calore. Anche nella lampadina il principale effetto del passaggio di corrente è il calore, che fa diventare incandescente il filamento, sviluppando di conseguenza energia luminosa. Un ferro da stiro o una stufetta elettrica sfruttano proprio questa proprietà. È detto effetto Joule, dal nome del fisico inglese James Prescott Joule (1818-1889) che lo scoprì, il fenomeno per cui il passaggio di corrente elettrica attraverso un conduttore è accompagnato dallo sviluppo di calore. La potenza dissipata da un resistore percorso da corrente di intensità I, e ai cui estremi è applicata una differenza di potenziale V, è data da: Dalla prima legge di Ohm: quindi la potenza si può scrivere: La quantità di energia elettrica che viene trasferita al resistore nell'intervallo di tempo t è quindi è pari a RI2t. Se tutta questa energia viene trasformata in calore, si ricava la quantità di calore Q prodotto da un conduttore di resistenza R, attraversato da una corrente I, nell'intervallo di tempo t: Il calore prodotto per effetto Joule quindi è direttamente proporzionale alla resistenza del conduttore e al quadrato dell'intensità della corrente che lo attraversa. Possiamo a questo punto definire la resistenza elettrica come l'attitudine di un conduttore a trasformare l'energia elettrica che lo percorre in calore. Quando in un apparecchio elettrico si richiede che la percentuale di energia elettrica convertita in calore sia molto alta, occorrerà aumentare il più possibile la resistenza dell'apparecchio. Questo avviene per esempio nelle stufe o nei ferri da stiro. In altri casi, invece, è essenziale che venga dispersa meno energia possibile e, benché non sia possibile eliminare completamente l'effetto Joule, si cerca di minimizzare il riscaldamento utilizzando materiali a bassa resistenza, come l'oro, l'argento o il rame. Per questo motivo i cavi che collegano tra loro gli apparecchi elettrici o quelli che portano l'elettricità nelle case sono di rame.

TENSIONE E CORRENTE

Per spiegare il significato di tensione usiamo un semplice esempio: due serbatoi di acqua sono collegati con un tubo. Se il livello A nel primo serbatoio è identico al livello B del secondo (prima figura), non si ottiene alcun movimento, mentre una differente altezza (seconda figura) provoca il passaggio di acqua dal serbatoio col livello più alto a quello col livello più basso. Si deduce che per ottenere il movimento si ha bisogno di una differenza di altezza.

Negli impianti elettrici al posto del tubo abbiamo il cavo elettrico e al posto dell'acqua abbiamo la corrente elettrica. La differenza non è più di altezza, ma di potenziale elettrico. Questa differenza di potenziale (d.d.p.) prende il nome di tensione.
Se aumentiamo la differenza di altezza, l'acqua scorre con più velocità. Allo stesso modo se aumentiamo la tensione aumenta l'intensità di corrente.

La differenza di altezza si misura in metri, mentre la differenza di potenziale (tensione) si misura in volt (V) e la indichiamo con la lettera V. La corrente si misura in ampere (A) e si indica con la lettera I.

La situazione mostrata nella figura precedente, può essere considerata simile a quella che si ha in una batteria. Infatti col passaggio di acqua la differenza di livello va progressivamente riducendosi fino ad annullarsi. Allo stesso modo una batteria si scarica (si riduce la differenza di potenziale tra polo positivo e polo negativo) mentre eroga corrente.

In una presa invece, vi sono costantemente 230 volt tra fase e neutro. Una situazione simile sarebbe quella in cui un rubinetto provvede a immettere continuamente acqua nel serbatoio per mantenere costante il livello A e di conseguenza la differenza A-B (possiamo considerare il livello B come quello del mare, sempre costante prescindendo dalle maree).

corrente elettrica è data dal movimento di elettroni nella stessa direzione

GENERATORE DI TENSIONE
Un dispositivo capace di generare una differenza di potenziale tra i suoi due terminali, prende il nome di generatore di tensione. Esistono due tipi di tensione che dobbiamo prendere in considerazione:

PANNELLI FOTOVOLTAICI Ottenere corrente elettrica dal Sole. Delucidazioni sugli impianti fotovoltaici: costi, risparmi, suggerimenti e rendimenti.
Cosa occorre comprendere prima di acquistare un impianto fotovoltaico: Ci sono realmente molte piccole cose che quotidianamente ci sfuggono, o che spesso dimentichiamo, fingendo che siano concetti per gli altri e non per noi....
la prima operazione da attuare in una abitazione è il risparmio energetico, che non significa tornare all'età della pietra, o diventare un ecologista estremista, ma semplicemente adottare dei piccoli coerenti accorgimenti, al fine di consumare meno e di non doversi dotare a tutti i costi di un impianto fotovoltaico ultra potente. Anche perchè si può arrivare facilmente a consumare la metà, e di conseguenza l'impianto solare costa a sua volta la metà! poi se avete soldi da buttare dalla finestra, allora è un altro discorso.....( speriamo di passare sotto quella finestra nel momento giusto... )

In pratica consigliamo vivamente questi piccoli accorgimenti:
usare SOLO lampadine a basso consumo, è vero: costano molto di più di quelle normali, ma durano molto di più, consumano molto di meno ed esistono ormai in molte forme diverse, quindi sono facilmente utilizzabili nei comuni lampadari o anche in quelli non-comuni.
spegnere gli elettrodomestici quando non sono in uso, questo vale per televisori, stereo hi-fi, videoregistratori, computer ecc., un esempio significativo: quella simpatica lucetta rossa dello stand by del televisore, ci può costare fino a 30 Euro all'anno inutilmente, e in più, in caso di temporali o di scariche elettriche, aumenta di moltissimo la probabilità di guasto del televisore stesso! molto importante questo discorso per il computer, scanner, stampanti ed altri accessori, che ormai spesso non hanno nemmeno più il bottone dello spegnimento, e quindi consumano energia inutilmente 24 ore su 24, quasi con il solo scopo di guastarsi prima: consigliamo una bella ciabatta elettrica con interuttore che stacca la corrente all'intero blocco computer: si risparmia in energia, si evitano spesso inutili guasti e si ha minore emissione di radiazioni elettromagnetiche inutili nel locale ( spesso il computer viene messo in camera da letto dei figli ! )
evitare di lasciare l'illuminazione accesa nelle stanze non occupate scegliere lampadari con minor numero di lampade : a parità di illuminazione prodotta, i lampadari con più lampade, consumano più energia rispetto a quelli con una lampada sola.
posizionare il frigorifero o il congelatore in luoghi aerati lontani da fonti di calore.
regolare il termostato dei frigoriferi o dei congelatori su un livello intermedio: posizioni più fredde comportano un aumento inutile dei consumi del 10-15%.
per le lavatrici: utilizzare ove possibile cicli di lavaggio a bassa temperatura
sostituire i vari elettrodomestici quando diventano vecchi, o si guastano, con elettrodomestici moderni e a basso consumo.

Con la semplice sostituzione delle lampadine e lo spegnimento dei vari televisori, computer ecc. otteniamo già un risparmio di più di 600-750 KWh, equivalenti anche a 150-200 Euro all'anno! soldi che possiamo usare tranquillamente per comprare le 'costose' lampadine a basso consumo ( le trovi in qualsiasi negozio serio di elettrodomestici o nei supermercati ), ma soprattutto possiamo permetterci un impianto solare di potenza inferiore di almeno 500 Wp sul totale, equivalenti ad almeno 2.000-3.000 Euro risparmiati.

Da fonte ENEA riportiamo questa tabella molto significativa:

Dai dati visualizzati si può osservare di quanto diminuiscano i consumi di energia elettrica grazie all'attenzione, e all'acquisto di prodotti ad alta efficienza.
Questa tabella può essere vista come regola per sostituire, man mano che diventano obsoleti, i vari elettrodomestici della nostra abitazione, in modo da riuscire ad ottenere una buona copertura del proprio fabbisogno elettrico annuale grazie all'energia solare.

Una volta capito quanto spendo, posso capire quanto posso, o voglio risparmiare, e che tipo di impianto acquistare.

Quale è la produttività di un impianto fotovoltaico per la produzione di corrente elettrica?
Il Sole può regalarci anche il 100% del fabbisogno di energia elettrica necessario alla nostra abitazione. Purtroppo gli impianti solari fotovoltaici hanno una resa molto più bassa degli impianti solari termici, che si usano per produrre acqua calda, e quindi occorre occupare una superficie maggiore del tetto.
A differenza degli impianti termici, che non possono essere troppo sovradimensionionati rispetto alle nostre necessità, altrimenti durante l'estate ci ritroveremmo con centinaia di litri di acqua bollente senza sapere cosa farne, gli impianti fotovoltaici possono venire dimensionati in modo da produrre tutta l'energia di cui abbiamo bisogno, visto che l'energia in surplus la possiamo cedere all'Enel, che poi ce la rende di nuovo quando ne abbiamo realmente bisogno.
In pratica l'Enel ci fa da grande serbatoio: sfrutta il surplus di energia prodotta in estate e ce la rende in inverno: cosa purtroppo non possibile con l'acqua calda.
Il rovescio della medaglia è che purtroppo gli impianti solari fotovoltaici costano ancora molto, quindi non sempre ci si può permettere un impianto sufficiente a coprire il nostro fabbisogno annuale di corrente elettrica.

Quanto risparmio annualmente?
In pratica ognuno di noi può decidere quanto risparmiare in corrente elettrica, semplicemente acquistando un impianto più o meno potente, in base ai consumi che annualmente abbiamo di corrente elettrica: è sufficiente prendere una bolletta Enel e capire quanti KWh consumiamo ogni anno.
In una casa dove vivono 4 persone e i consumi sono oculati, quindi le lampadine sono a basso consumo, non sono presenti condizionatori, il riscaldamento e i fornelli sono a metano, e non si lasciano accese le lampadine per ore ed ore inutilmente, normalmente vengono consumati 1.500-2.500 Kwh all'anno.
Mentre in un'abitazione di 4 persone, dove non ci sono le condizioni dette sopra, i consumi annui sono di circa 3.000-4.000 KWh.
La media dei consumi di una tipica famiglia italiana è di 3.000-4.000 KWh/anno, quindi si può intuire che sono ben poche le famiglie che adottano misure per il risparmio energetico.

Quanto spendo per l'impianto solare fotovoltaico e per la manutenzione?
Gli impianti fotovoltaici normalmente vengono venduti in base ai KWh che producono in condizioni di irraggiamento ideale.
Un impianto base è quello da 1.200 Wp ( significa che in condizioni ottimali produce 1.200 Watt di picco ) e produce, se installato nel Nord Italia circa 1.300 / 1.500 KWh/anno, mentre nel Sud Italia 1.600-2.000 KWh/anno.
Un impianto del genere costa circa 6.500 Euro iva, installazione e trasporto inclusi.
Mentre un impianto da 2.000 Wp costa circa 9.000 Euro iva, installazione e trasporto inclusi.
L'installazione può venire a costare 500-1.500 Euro, a seconda delle difficoltà che si possono incontrare.
Al costo comunque dell'intero impianto si può detrarre il recupero dell'IRPEF del 36%, che significa uno sconto del 36% sull'intera spesa, oltre a possibili finanziamenti o contributi per l'installazione di impianti fotovoltaici.
Questi tipi di impianti solari non necessitano di una particolare manutenzione, volendo si possono pulire i vari pannelli fotovoltaici ogni 2-3 anni, anche se normalmente gli stessi si mantengono abbastanza puliti grazie alla pioggia e al vento.
Occorre invece magari osservare, di tanto in tanto, le spie presenti sull'inverter, che possono segnalare eventuali guasti, o anomalie nel rendimento, ed eventualmente chiamare l'elettricista di fiducia, per trovarne le possibili cause.

Quanto impiego ad ammortizzare l'impianto?
Il calcolo in questo caso non è particolarmente semplice, comunque considerando un vita minima dell'impianto solare di 30 anni, le spese di eventuali manutenzioni, l'aumento del costo delle stesse e dell' energia elettrica nel futuro, il tutto in base all'inflazione: un impianto da 1.200 Wp consente un risparmio di 300-550 Euro / anno se posto nel Nord Italia, mentre se posto nel Sud Italia, il risparmio diventa di 350-650 Euro / anno.
Un impianto solare dura tranquillamente 30 anni, quindi se teniamo conto delle spese, del risparmio e del recupero del 41% di IRPEF, impiegheremo per ammortizzarlo circa 6-12 anni ( nel Sud Italia occorre meno tempo per ammortizzare l'impianto, visto l'irraggiamento solare superiore ), mettendo già in conto i futuri aumenti del costo dell'energia elettrica.

Ma se posseggo una linea elettrica da 3KW di potenza, devo dotarmi di un impianto fotovoltaico da 3 KWp?
Questa è una domanda frequentissima, e la risposta è: assolutamente no!
L'impianto fotovoltaico fornisce un'energia quasi costante che viene immessa in maniera continua nella rete Enel finchè c'è il Sole. Il circuito solare è quasi un circuito a parte, mentre la corrente elettrica che occorre per l'abitazione viene prelevata direttamente dall'Enel: in questa maniera ho a disposizione una potenza molto elevata ( 3 KW o più) ogni volta che ne ho bisogno.
Un circuito solare di 1.200 Wp può produrre energia sufficiente per coprire un'abitazione con un consumo annuale di circa 2.000 KWh, quindi un'abitazione di 3-4 persone con attenti consumi elettrici.
Mentre per un'abitazione dove i consumi non sono proprio 'oculati' si può pensare ad un impianto fotovoltaico da 2.000-2.400 Wp, ma in linea di massima non è mai consigliato un impianto fotovoltaico da 3.000 Wp, in quanto in questo caso si rischierebbe di produrre inutilmente più energia di quanta ne è necessaria, e in questo momento l'enel non ce la pagherebbe, ma la terrebbe in accredito per l'anno successivo, con il rischio effettivamente di perderla.

Posso vendere corrente all'Enel?
In questo momento NO, posso solo cederla e pago solo la differenza tra quello che consumo e quello che produco.
Se produco più corrente di quella che consumo, tale eccesso sarà conteggiato nell'anno successivo, ma non verrà in alcun modo pagato dall'Enel.

Quale tipo di impianto scelgo?
Innanzitutto occorre stabilire, in base alla zona dove si vive, o in base alle proprie convinzioni ecologiste, che tipo di modulo fotovoltaico si vuole usare: in questa pagina puoi vedere le principali differenze, i vantaggi e gli svantaggi dei moduli fotovoltaici in silicio amorfo, rispetto a quelli in silicio monocristallino o policristallino, e viceversa.

Entrando invece nel merito degli impianti solari fotovoltaici, ne esistono fondamentalmente di due tipi:
Impianto a moduli fotovoltaici con connessione alla rete elettrica Enel ( grid connected ) questi tipi di impianti solari fotovoltaici producono corrente elettrica che viene immessa, una volta convertita in corrente alternata a 220 Volt, nella rete Enel, per essere usata nella tua città. Questo avviene attraverso un contatore speciale installato dall'Enel: in questa maniera non necessitiamo di costose batterie per conservare l'energia elettrica prodotta, ma la possiamo riprendere dall'Enel in qualsiasi momento, pagando solo la differenza tra quella prodotta e quella consumata.

Scambiare corrente con l'Enel ha un costo di circa 30 Euro l'anno, perchè questo è il costo per il noleggio del contatore di acquisto dell'energia prodotta dai moduli fotovoltaici.
Quindi come soluzione non è molto dispendiosa, se si considera che invece fornirsi di batterie può costare facilmente anche 1.000 Euro, oltre alle problematiche di usura delle batterie stesse che hanno una vita di circa 10-15 anni.
Dotarsi di batterie è abbastanza sconsigliato anche perchè purtroppo le batterie saranno cariche al massimo durante i mesi estivi, quando magari non necessitiamo di molta energia elettrica, o siamo in vacanza, mentre faranno fatica a caricarsi durante i mesi invernali, proprio quando serve più energia nell'abitazione.

Impianto a moduli fotovoltaici per utenze isolate ( stand alone ) questi tipi di impianti solari fotovoltaici producono corrente elettrica, che viene utilizzata per caricare delle batterie, normalmente a 12-24 Volt, in modo da poter utilizzare l'energia elettrica, prodotta dai moduli fotovoltaici, in un qualsiasi momento della giornata.
Normalmente questi tipi di impianti sono usati laddove l'Enel non arriva con i propri cavi, quindi baite di montagna, o case in campagna, oppure nel caso ci si voglia staccare completamente o parzialmente dall'Enel.
Anche se in realtà, staccarsi completamente dall'Enel, può creare seri problemi nel momento in cui ci siano guasti, o giornate particolarmente nuvolose, oltre al fatto che comunque in linea di massima, da un punto di vista ecologico e pratico è più conveniente cedere l'energia prodotta direttamente all'Enel, piuttosto che conservarla in batterie costose e che una volta in disuso diverranno materiale altamente inquinante.
Si possono utilizzare lampade, frigoriferi o apparecchiature speciali che, funzionando a 12-24 Volt, non necessitano dell'inverter per funzionare.
Altrimenti, se è indispensabile usare corrente elettrica a 220 Volt, è necessario anche installare un inverter, il cui compito è di trasformare la corrente delle batterie in corrente alternata a 220 Volt.
Occorre tenere in considerazione, in questo caso, che non è più necessario acquistare un inverter di tipo professionale ( che richiede l'Enel ), ma ne basta un modello abbastanza economico.

Scottature da corrente elettrica

La corrente elettrica può provocare ustioni perché passando attraverso la cute e i tessuti sottocutanei li surriscalda e provoca un'alterazione simile a quella causata dal fuoco. L'ustione da elettricità però spesso non è visibile, perché colpisce i tessuti in profondità. Quindi chi ha subito una lesione elettrica riceverà una terapia diversa da chi ha avuto altri tipi di ustione.

• Fate controllare la sicurezza del vostro impianto elettrico. Alcune prese vecchie potrebbero non avere la messa a terra. Non fate riparazioni elettriche da soli, a meno che non siate abbastanza esperti per farle in sicurezza.
• Non estraete le spine tirandole dal filo e fissate le prese che tendono a staccarsi dal muro.
• Controllate che i fili elettrici siano ben isolati. Non fateli passare sotto tappeti o a contatto con tessuti.
• Usate il meno possibile gli adattatori a più prese e le prese multiple. Il sovraccarico potrebbe causare scintille.
• Staccate la corrente, prima di cambiare le lampadine.
• Non toccate spine, prese o interruttori con le mani bagnate.
• Non appoggiate phon, rasoi elettrici, stufette, radio e altri apparecchi sul bordo del lavandino o della vasca, perché potrebbero cadere nell'acqua. Non usateli con le mani bagnate o con i piedi nudi (l'acqua è un ottimo conduttore dell'elettricità), ma indossate ciabatte o scarpe con la suola di gomma.
• Se un apparecchio elettrico si incendia, non gettategli sopra acqua, perché rischiate di prendere la scossa. Spegnete le fiamme soffocandole con una coperta, meglio se di tessuto ignifugo (ossia antincendio).

DOMANDE RISPOSTE

qual'è la natura della corrente elettrica altenata?

come funziona il sistema elettrico dall'altra parte del mondo? Devo comprarmi degli adattatori?

Come forma basta che prendi un adattatore consono, per quanto riuguarda frequenza e tensione, anche loro vanno a 50Hz sl che hanno 30V in + di noi (250 contro 220) per cui ti conviene controllare sugli apparecchi che intendi utilizzare se funzionano anche a 250 o rischi di fonderli.

Continuo a prendere la "scossa" di elettricità statica in qualsiasi oggetto metallico ( e non ) io tocchi... al lavoro con i clienti li fulmino come un centralina dell'enel quando li sfioro.
Sò già che il fenomeno deriva dall'elettricita statica che si scarica dagli indumenti di lana o acrilici o sintetici... ma mi sapete dire una maniera per convogliarla e accendere una lampadina che tengo in bocca? no ... scherzo mi basterebbe non fulminare i clienti.

Non riusciresti ad accendere una lampadina nemmeno sfregando insieme tutte le pecore della patagonia.
A parte gli scherzi, o cambi indumenti, o metti scarpe conduttive (solo se il pavimento non e' isolante) o umidifichi l'ambiente dove lavori o cambi il tipo di pavimentazione specie se e' di moquette ( un generatore di statica favoloso) oppure un paio di volte al giorno tocca un calorifero , dove non e' verniiciato , per scaricarti
Ci sono delle norme precise sulla prevenzione degli incidenti sul lavoro causai dalle cariche statiche ma solo se lavori in ambienti a rischio a contatto con gas infammabili o strumenti delicati

Quiz! Tensione e corrente elettrica

		La corrente elettrica è costituita da un qualsiasi movimento di cariche dal movimento delle sole cariche positive da cariche positive e da cariche negative che si muovono nello stesso senso delle cariche negative da cariche di segno opposto che si muovono in senso opposto da un accumulo di cariche negative Lasciare senza risposta
		La tensione elettrica è la forza che agisce sull´unità di carica elettrica la potenza della corrente elettrica il lavoro fatto dall´unità di carica la capacità di creare carica elettrica la quantità di carica che si sposta tra due punti Lasciare senza risposta
		L´intensità di corrente è la quantità di carica che attraversa una sezione di conduttore la quantità di elettricità che attraversa la sezione di un conduttore nell´unità di tempo il numero di cariche che attraversa la sezione di un conduttore in un tempo prefissato il prodotto della carica che ha attraversato la sezione per il tempo il rapporto tra l´energia delle cariche e la loro velocità di spostamento Lasciare senza risposta
		L´intensità di corrente è esprimibile dimensionalmente con [C][s] [V][s] [C]/[V] [C]/[s] [J][C] Lasciare senza risposta
		La tensione elettrica è esprimibile dimensionalmente con [A][s] [J]/[C] [C]/[s] [J][s] [J][C] Lasciare senza risposta
		Il potenziale elettrico è la forza dell´unità di carica positiva in un punto a meno di una costante l´enegia assoluta della carica positiva in un punto la possibilità di creare ogni tipo di carica elettrica l´energia dell´unità di carica positiva in un punto a meno di una costante il rapporto tra la corrente e la carica in un punto Lasciare senza risposta
		Un generatore elettrico genera cariche elettriche positive genera cariche elettriche negative separa le cariche elettriche aumenta le carica elettrica di un circuito diminuisce la carica negativa di un circuito Lasciare senza risposta
		Il segno positivo dell´intensità di corrente significa che nel circuito le cariche positive e negative si muovono nel senso prefissato le cariche negative si muovono nel senso prefissato le cariche positive si muovono in senso contrario a quello prefissato le cariche negative si muovono in senso contrario a quello prefissato le cariche positive hanno movimento opposto a quello delle cariche negative Lasciare senza risposta
		La forza elettromotrice di un generatore è la forza che agisce sulle cariche elettriche la quantità di carica separata tra i due morsetti la forza esistente tra i suoi morsetti la tensione tra le cariche in movimento l´energia da esso fornita all´unità di carica positiva Lasciare senza risposta
		Il segno positivo di una tensione elettrica tra due punti ( si consideri come primo punto quello dal quale entra la corrente) si ha quando la corrente elettrica nel primo punto è maggiore della corrente elettrica nel secondo punto la carica elettrica nel primo punto è maggiore della carica elettrica nel secondo punto l´energia della unità di carica positiva nel secondo punto è inferiore all´energia dell´unità di carica nel primo punto la velocità delle cariche nel primo punto è superiore a quella che le cariche hanno nel secondo quando l´unità di carica positiva acquista energia nel passare da un punto all´altro Lasciare senza risposta Fine modulo