|
|
| |
RELAZIONE DI ELETTRONICA
Realizzata da: Curletta Daniele, Falcioni Silvia, Falzetti Marta, Torresetti Simone.
Classe: 3°G
Voglio costruire un circuito capace di prendere un bit A e un bit B e li sappia sommare ed eventualmente indicare il riporto.
![]()
![]()
![]()
![]()
![]()
![]()
![]() 646e42g
646e42g
646e42g B1 A1 C1 646e42g 646e42g B0 A0


646e42g F.A. 646e42g 646e42g H.A.
646e42g Sommatore 646e42g 646e42g Mezzo 646e42g
646e42g Completo 646e42g 646e42g Sommatore
646e42g S1 646e42g 646e42g 646e42g S0
646e42g 646e42g
646e42g C2 646e42g 646e42g C1
![]()
![]()
Dato un problema non ambiguo costruiremo in questo problema una tabella di verità, poi ci ricaveremo la funzione canonica che verrà tradotta in un circuito elettronico digitale.
Oppure costruita la tabella di verità si può passare direttamente con l'algebra di Boole o le mappe di Karnaught per ottenere una funzione semplificata, che ci darà un circuito digitale. 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g
I circuiti elettronici vengono normalmente distinti in due categorie:
a) circuiti analogici;
b) circuiti digitali;
La differenza deriva dalle caratteristiche dei segnali con cui lavorano questi circuiti.
Si ha un segnale analogico quando questo può variare con continuità, assumendo nel tempo tutti i valori compresi in un certo intervallo.
Si ha invece un segnale digitale quando questo non varia con continuità, ma può assumere solo valori ben determinati.
Il caso più diffuso di segnale digitale è quello binario. Ai due possibili valori del segnale binario si associano convenzionalmente i numeri 0 e 1.
Si definisce variabile logica binaria una variabile che può assumere solo due valori a cui si fa corrispondere, convenzionalmente, lo stato logico 0 e lo stato logico 1.
I circuiti combinatori rispondono in uscita tenendo conto solo degli ingressi e non dello stato. I circuiti sequenziali dipendono dall'ingresso attuale e precedente che ha creato lo stato del sistema.
L'algebra booleana ideata da George Boole (1815-1864) si adatta all'elettronica digitale binaria, con la sostituzione dell'affermazione vera/falsa con i valori 1/0.
L'algebra di Boole si basa sui seguenti assiomi:
0+0=0
0+1=1
1+0=1
1+1=1
646e42g 646e42g 1=0 646e42g 0=1
Quindi secondo i criteri dell'algebra booleana ci siamo costruiti le tabelle di verità per l'Half Adder e per il Full Adder e le relative mappe di Karnaugh:
646e42g 646e42g 646e42g 646e42g 646e42g 646e42g
646e42g 646e42g 646e42g HALF ADDER
646e42g
|
B0 |
A0 |
S0 |
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g
646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g
1 0
1
|
![]()
S0 = (A0 * B0) + (A0 * B0)
|
![]()
|
|
|
|
|
|
C1= A0
* B0
![]()
B 1 A
|
|
|
|
|
646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g
646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g
|
B1 |
A1 |
C1 |
S1 |
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
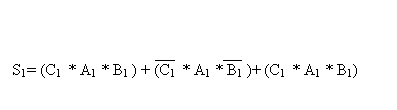
A
B 0 1
![]()
![]()
![]() 646e42g 646e42g 646e42g 646e42g
0 0 0 1 1 1 1 0 646e42g 646e42g 646e42g
646e42g 646e42g 646e42g 646e42g
0 0 0 1 1 1 1 0 646e42g 646e42g 646e42g
|
|
|
|
|
|
|
|
|
|
646e42g 646e42g
C2= ( A1 * C1 ) + ( A1
* B1 ) + (C1 * B1 ) A
B 0 1
![]() 646e42g
646e42g
![]() 646e42g 646e42g 646e42g 646e42g 0
0 0 1 1 1 1 0 646e42g 646e42g 646e42g
646e42g 646e42g 646e42g 646e42g 0
0 0 1 1 1 1 0 646e42g 646e42g 646e42g
|
|
|
|
|
|
|
|
|
|
646e42g 646e42g
Dalle tabelle della verità siamo potuti risalire ai seguenti circuiti elettrici:
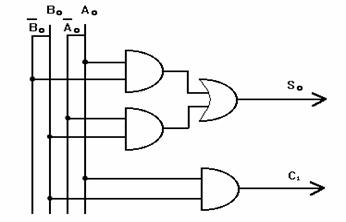
C1 B1 A1
FULL ADDER
S1 C2
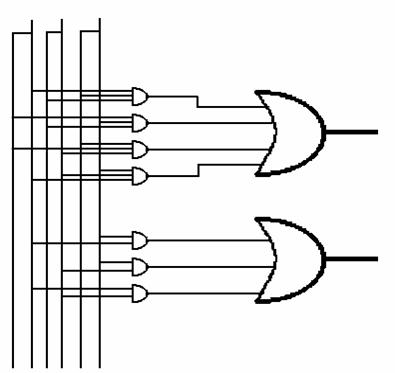
A questo punto abbiamo costruito il circuito elettrico seguendo i disegni da noi eseguiti e cioè applicando sulla breadboard gli integrati and o or a seconda delle porte logiche. Successivamente abbiamo collegato con dei fili i piedini degli integrati tra di loro osservando le entrate e le uscite in un manuale. Poi abbiamo aggiunto due resistenze e due led luminosi per le uscite (S0 ,C1, S1,C2 ).
Infine abbiamo provato le combinazioni delle entrate e abbiamo osservato che i collegamenti erano stati ben eseguiti e poiché per ogni entrata avevamo un'uscita.
646e42g 646e42g
646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g
646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g
646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g
646e42g 646e42g 646e42g 646e42g 646e42g 646e42g 646e42g
646e42g 646e42g 646e42g 646e42g
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026