 |  | |
|
| | |
|
| |
CIRCUITI INTEGRATORI
Un'applicazione della funzione integrale è realizzata da un dispositivo elettronico chiamato Integratore.
Il componente che da origine all'integrazione è il condensatore in cui la corrente , proporzionale alla capacita C, dipende dalla variazione nel tempo della tensione che si stabilisce ai capi del condensatore stesso.
INEGRATORE IDEALE in configurazione invertente
Si consideri un amplificatore operazionale nella configurazione invertente nella quale l'impedenza di reazione sia costituita da una capacità C, mentre quella di ingresso da una resistenza R.
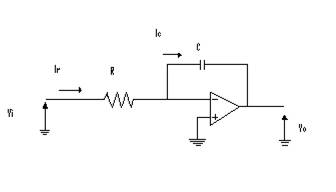
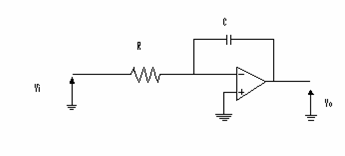
Le caratteristiche princip 959g67j ali di questo circuito sono:
La resistenza d'ingresso dell'operazionale è infinita: RiAO=∞
La corrente del morsetto invertente è uguale alla corrente del morsetto non-invertente che è nulla I-=I+=0
La tensione invertente e non-invertente per il concetto di massa virtuale sono nulle. V-=V+=0
Essendo I- = 0 allora Ic = Ir
Andiamo a determinare le correnti Ic e Ir:
In precedenza è stato affermato che V-=V+=0, quindi, se V- = 0, avremo:
Essendo Ic = Ir si uguaglieranno le due correnti:
Per calcolare V0 occorrerà integrare entrambi i membri:
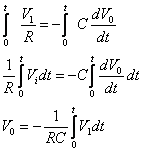
N.B.
L'integrale è definito a meno di una costante "c" che rappresenta l'eventuale carica iniziale del condensatore;
Il segno meno indica lo sfasamento di 180°.
CALCOLO DELLA FUNZIONE DI TRASFERIMENTO nel dominio "s"
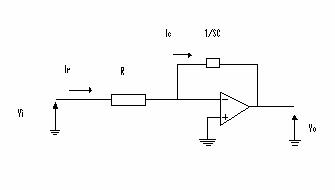
Essendo in configurazione invertente la funzione di trasferimento è molto semplice da definire:
Se 
e R2=R, il
rapporto tra tensione d'uscita e tensione d'ingresso sarà:
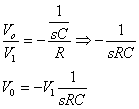
CALCOLO DELLA FUNZIONE DI TRASFERIMENTO nel dominio della frequenza.
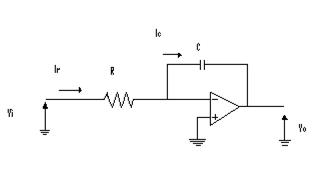
Partendo dalle condizioni iniziali per cui V-=V+=0 e Ic = Ir, avremo che :
E quindi
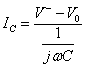E quindi 
Sapendo che Ic = Ir potremmo dire che:
INTEGRATORE REALE in configurazione invertente
La funzione di trasferimento ideale in dominio della frequenza è:
e l'equivalente modulo
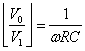
Bisogna notare che nel caso in cui 
il modulo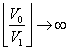
e quindi il dispositivo si porta in saturazione.
Se al segnale V1 ei sovrappone
un disturbo in bassa frequenza il dispositivo si porta in saturazione. In altri
termini se f=0 la reattanza 
Ciò equivale a
considerare il condensatore un circuito aperto; ne consegue che
l'amplificatore operazionale diventa a catene aperta con un guadagno infinito.
In queste condizioni anche un piccolissimo disturbo riesce a portare
l'amplificatore operazionale in saturazione. Per evitare ciò si pone una
resistenza in parallelo al condensatore C. In tal modo quando vi sono delle
condizioni per le quali
resta un
amplificatore nella connessione del tipo
a guadagno 
INTEGRATORE REALE
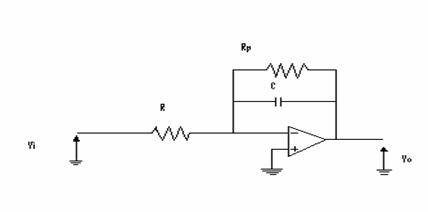
Partendo dalla condizione 
accadrà che 
alla frequenza di
lavoro.
A questo punto la funzione di trasferimento, considerando la configurazione invertente dell'amplificatore operazionale, è data da:
Dove 
e 
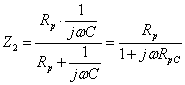
Quindi:
ed in modulo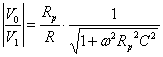 
Al variare di ω si ha:
Per
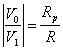
Il circuito si comporta da amplificatore
invertente a guadagno 
;eventuali disturbi vengono amplificati senza portare il
dispositivo in saturazione. Questa condizione resta valida finchè:
da cui 
Per
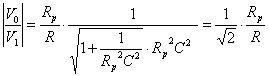
Il modulo del guadagno si riduce di√2 ovvero di 3db ( attenuazione del 30%).
Per
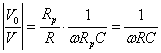
In
questo caso il rapporto
coincide con la
funzione di trasferimento di un integratore ideale.
Ciò è verificato anche per da cui
In definitiva:
Per
il circuito si
comporta da amplificatore invertente:
Per
il circuito si
comporta da integratore.
Il diagramma di Bode del modulo della funzione di trasferimento di un integratore reale è:
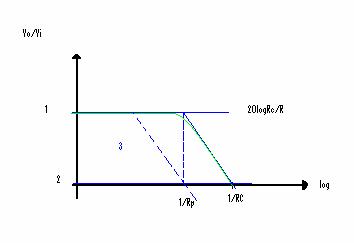
Il modulo della funzione di trasferimento in db è dato da:
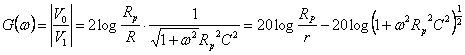
Il diagramma di Bode è il risultato della somma delle due
componenti della 
La prima 
è una costante che
raggruppa una retta per 
per 
La seconda 
da:
per
per
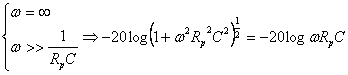
Questa ultima è una retta a pendenza negativa che taglia l'asse delle ascisse
per 
e presenta una
pendenza di 20db/decade.
Andando a studiare il modulo della funzione di trasferimento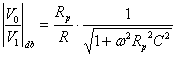 
si possono incontrare tre casi, a seconda del valore di 
,infatti:
se
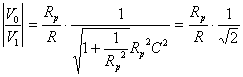
In pratica il modulo si attenua del 30% ovvero di 3db.
Per
ovvero per
si ha:
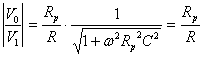
Il circuito si comporta da amplificatore invertente.
Per
ovvero per 
Si ha:
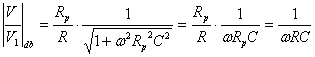
Il circuito si comporta da integratore ideale invertente.
Per diminuire Rp esistono due metodi:
Dal diagramma di Bode si nota che
il dispositivo si comporta da integratore alle alte frequenze, per allargare
quest'intervallo deve risultare 
molto piccolo. Si
pone pertanto 
Il dispositivo si comporta da
integratore ideale quando 
da cui 
In altri termini quando il circuito si
comporta da integratore la Rp costituisce un circuito aperto rispetto alla
reattanza capacitiva 
.
INTEGRATORE IDEALE in configurazione non invertente
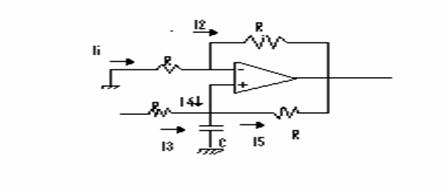
Il segnale in uscita V0 è sfasato di 90° gradi in ritardo rispetto a V1.
AL MORSETTO INVERTENTE si ha:
e
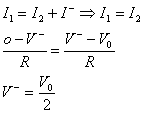
AL MORSETTO non-INVERTENTE si ha:
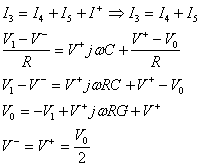
F.d.t nel dominio della frequenza:
F.d.t nel dominio del tempo:
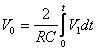
F.d.t nel dominio della variabile "s":
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025
