|
|
| |
A 0 K ( Kelvin ) i semiconduttori si comportano come isolanti, poiché nessun elettrone ha abbastanza energia da poter comparire nella banda di conduzione.
Ciò che permette il fenomeno del passaggio della banda di conduzione è intuitivamente la temperatura. Per temperature maggiori di 0 K ( Kelvin ) alcuni elettroni acquisiscono un energia termica tale da spostarsi nella banda di conduzione. L'elettrone che migra lascia nella banda di valenza una LACUNA
Gli elettroni liberi possono essere spostati anche con un piccolissimo campo elettrico.
Nei metalli la corrente è dovuta esclusivamente dal flusso di elettroni.
Nei semiconduttori la corrente deriva dal movimento degli elettroni e anche dalle lacune.
La velocità media degli elettroni in un conduttore sottoposto a campo elettrico è:
v mE m = mobilità dell'elettrone
Se in un tratto di conduttore di lunghezza L sono presenti N elettroni che lo percorrono in un tempo T, l'intensità di corrente è:
I = Nq = Nqv
T L
La densità di corrente è : J = I = Nqv
A LA
Essendo LA il volume che contiene gli N elettroni, si ricava :
n =_N_ elettroni concentrazione elettronica
LA _ cm
Possiamo dunque riscrivere l'espressione della densità di corrente: J = nqv
dalla quale si può ricavare la CONDUTTIVITA' del metallo. Infatti:
J = nqv = nqmE s = nqm J = sE
Si nota dunque che s è proporzionale a n.
Come detto, nei semi conduttori la corrente è dovuta allo spostamento oltre che di elettroni, anche di lacune.
Quando la temperatura del semiconduttore è diversa da 0 K ( Kelvin ), alcuni legami covalenti si romperanno lasciando liberi degli elettroni di vagare per il cristallo e quindi per l'intera struttura cristallina. Ogni elettrone libero lascia un buco o lacuna. Tale lacuna contribuisce alla conduzione poiché essa tenderà ad essere riempita da un elettrone di valenza di un atomo vicino e così via, così da causare lo spostamento della lacuna è quindi uno spostamento di elettroni nel verso opposto. Tale meccanismo di conduzione elettrica non coinvolge elettroni liberi.
In un semiconduttore intrinseco n = p = ni dove n è la concentrazione degli elettroni, p quella delle lacune e ni è la CONCENTRAZIONE INTRINSECA. Vale dunque la relazione nipi = ni
dove ni cm a T = 300 K. La suddetta relazione vale all'equilibrio termico e in assenza di tensioni applicate.
Per regolare i fenomeni di conduzione dei semiconduttori intrinseci, ad essi di aggiunge una certa quantità di DROGANTE, così da ottenere un semiconduttore drogato. Tale operazione si effettua portando la temperatura del semiconduttore ( in questo caso il silicio ) ad una temperatura non troppo distante da quella di fusione ed esponendo un lato della striscia del semiconduttore ( con spessore di 1mm e lunghezza standard di 300 mm ) a un gas di drogante, che varia a seconda del tipo di drogaggio desiderato.
È possibile drogare con DONATORI ( atomi pentavalenti ) con i quali quattro dei cinque elettroni di valenza andranno ad occupare dei legami covalenti del semiconduttore ( che è tetravalente ), mentre quello in eccesso sarà libero e quindi disponibile come portatore di corrente. Essendo gli elettroni portatori negativi, tale semiconduttore drogato sarà di TIPO N. Per tale tipo di drogaggio si usa l'antimonio, il fosforo e l'arsenico. Con le impurità donatrici di un semiconduttore vengono introdotti nuovi livelli energetici, consentiti, di energia appena inferiore a quella della banda di conduzione. Con l'energia termica assunte a temperatura ambiente praticamente tutti gli elettroni liberi del donatore raggiungono la banda di conduzione. Oltre al drogaggio suddetto è possibile quello con ACCETTORI ( atomi tetravalenti ) con i quali solo tre dei quattro legami covalenti del semiconduttore potranno essere occupati. L'assenza che si ha nel quarto legame costituisce una lacuna: sarà dunque disponibile un ulteriore portatore negativo di corrente. Da ciò tale semiconduttore drogato si dirà di TIPO P. Con le impurità accettatrici in un semiconduttore vengono introdotti livelli energetici, consentiti, di energia appena superiore a quella della banda di valenza. A temperatura ambiente gli elettroni in banda di valenza hanno energia termica sufficiente per andare ad occupare tali lacune, le quali si sposteranno in banda di valenza e costituiranno la maggior parte dei portatori nel materiale semiconduttore. A causa del maggior numero di elettroni (n) o lacune (p), si ha una maggiore velocità di ricombinazione ( elettroni che colmano una lacuna ), per cui si ha una diminuzione del numero di lacune ( nel semiconduttore n ) o elettroni ( nel semiconduttore p ). Ciò che è vero è che in condizioni di equilibrio termico si ha che:
n p = ni LEGGE DELL'AZIONE DI MASSA
in cui ni è funzione della temperatura ed è indipendente dalle quantità di impurità.
In un semiconduttore drogato vale:
NA + n = ND + p RELAZIONE DELLA NEUTRALITA' DELLA CARICA
In un materiale di tipo n si ha che n >> p, dunque nn = ND
Per ottenere la concentrazione di lacune in tale materiale (pn), sapendo che
n p = ni pn = _ni = _ni
nn ND
Analogamente, per un materiale di tipo p si ha che p >> n, dunque pp = NA np = ni = _ni
p NA
se il semiconduttore è drogato con eguali concentrazioni di donatori e accettori, esso rimane INTRINSECO
Nei semiconduttori, a differenza dei metalli, esistono due meccanismi di trasporto delle cariche. Esistono infatti una CORRENTE di DRIFT e una CORRENTE di DIFFUSIONE. Quella di drift è del tutto analoga a quella nei conduttori, infatti è quella dovuta alle cariche libere. Essendo i portatori nei semiconduttori di due tipi ( elettroni e lacune ) è necessario definire due correnti di drift. Più precisamente in questo caso si farà riferimento alla DENSITA' di CORRENTE di DRIFT
Jp = qpmpE
che hanno versi concordi. Infatti le cariche negative avranno verso opposto al campo; le cariche positive avranno verso concorde al campo, ma questo corrisponde ad un conseguente movimento di elettroni nel verso opposto delle lacune. Si definiscono inoltre la CONDUCIBILITA'
![]() sp = qpmp per le lacune
sp = qpmp per le lacune
sn = qnmn per gli elettroni
Volendo, è possibile esplicitare la CONDUCIBILITA' TOTALE stot = q(pmp + nmn
e dunque anche la DENSITA' DI CORRENTE TOTALE J = stotE
La corrente di diffusione è dovuta alle variazioni di concentrazione di portatori di carica. Infatti le particelle tendono a migrare nelle aree in cui la loro concentrazione è minore ( tale fenomeno è detto diffusione ). Quindi la DENSITA' della CORRENTE di DIFFUSIONE è proporzionale al gradiente della concentrazione delle particelle. Se supponiamo che in una data superficie si abbia una diminuzione di concentrazione ( da sinistra verso destra ), si avrà un gradiente negativo:
![]() Jp = -qDpdp
Jp = -qDpdp
Il segno cambiato è dovuto dal fatto che per Jn si considerano cariche negative ( -q ). Nelle equazioni appena viste compaiono anche termini Dp e Dn detti COSTANTI di DIFFUSIONE, ottenibili dalle relazioni di Einstein:
Dp = kbTmp Dn = kbTmn
q q
Notare che nel caso della diffusione Jp =
qFp e Jn = -qFn, dove Fp e Fn sono le DENSITA' di FLUSSO di lacune ed
elettroni, e si ottengono da:
Volendo esprimere in maniera generale la densità di corrente in un semiconduttore, otteniamo che:
![]()
Jp = qmppE - qDpdp(x)
Jn = qmnnE + qDndn(x)
Jtot = Jn + Jp
In tale rappresentazione si nota che la CORRENTE di DRIFT è dipendente dal campo elettrico, mentre la CORRENTE di DIFFUSIONE è dipendente dal gradiente di concentrazione.
Un semiconduttore
può essere drogato in modo ( idealmente ) uniforme o in modo non uniforme. In
quest'ultimo caso la concentrazione di portatori sarà in funzione di x. Se
consideriamo una tale situazione senza che tale pezzo di materiale sia eccitato
dall'esterno, per ciò che è stato detto prima, si avrà una corrente di
diffusione. Le condizioni al contorno impongono però una corrente nulla
attraverso il semiconduttore, ragion per cui dovrà esserci una corrente di
drift ad essa opposta.
movimento elettronico si ha solo in presenza di campi elettrici: questo rende
plausibile l'introduzione di un campo elettrico interno e una conseguente
differenza di potenziale attraverso il pezzo di materiale drogato.
Considerando il caso di un materiale drogato di tipo p. Si ha Dp mpVT e, sapendo essere la corrente nulla, Jp = qmppE-qDpdp(x) E = VT dp(x) CAMPO ELETTRICO
dx p dx INTERNO
Dunque, conoscendo p(x) è possibile ottenere E(x) all'interno del materiale. Per ottenere la variazione di potenziale tra due punti del pezzo di materiale, basta sapere che E = -grad(V) = dV
dalla quale otteniamo la relazione dV = -VT dp(x) dx
dx
A questo punto per ottenere la differenza di potenziale tra due punti è sufficiente integrare ambo i membri. I punti saranno X (in corrispondenza del quale la concentrazione è p e il potenziale è V ) e X ( con p e V ), ottenendo V - V = VT[ln(p )- ln(p
Si noti l'indipendenza della distanza dei due punti. È possibile dire che:
p = p eDV/VT RELAZIONE di BOLTZMANN
Se consideriamo un pezzo di semiconduttore avente volume V contenuto da una superficie S allora:
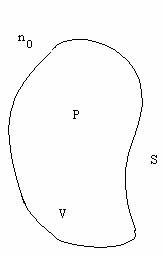
![]() P ( numero di lacune ) = pdV
P ( numero di lacune ) = pdV
La variazione nel tempo del numero di lacune P è dato da:
dP = d pdV integrale volumetrico
Una variazione di P può essere causato dal fatto che se c'è ad un lato del pezzo di materiale un certo numero di cariche entranti, dall'altro lato uscirà un numero diverso di cariche rispetto a quelle entrate. Tale differenza è dovuta dal fatto che all'interno del semiconduttore si verificano fenomeni di generazione e ricombinazione di coppie di portatori. Omettendo vari passaggi si ha che in equilibrio termodinamico:
![]() dP + (R-G) + 1 div(Jp nel caso delle lacune
dP + (R-G) + 1 div(Jp nel caso delle lacune
dt q
dn + (R-G) - 1 div(Jn nel caso degli elettroni
dt q
dove G è il numero di coppie generate nell'unità di volume e di tempo, mentre R è il numero di coppie che si ricombinano nell'unità di volume e di tempo. Analizzando il termine G, è possibile dire che G = Gth + G' dove Gth è il numero di coppie generate per effetto termico e G' è il numero di coppie generate per altri effetti. Dunque R - G = R - Gth - G'.
Possiamo ora isolare la variazione della concentrazione delle coppie non considerando l'effetto termico attraverso una variabile U = R-Gth. Per cui R-G = U-G'..
È possibile scrivere ora l'EQUAZIONE di CONTINUITÀ
![]() dP + U + 1 div(Jp) = G'
dP + U + 1 div(Jp) = G'
dt q
dn + U - 1 div(Jn) = G'
dt q
Come altro aspetto, volendo esprimere la DENSITÀ di CARICA TOTALE del materiale:
r = q( ND - NA + p - n )
Per terminare il quadro delle equazioni che determinano il COMPORTAMENTO dei DISPOSITIVI a SEMICONDUTTORE (lineari) introduciamo l'EQUAZIONE di POISSON
grad (V) = _ r
e er
e come già visto l'EQUAZIONE di QUASI STAZIONARIETÀ
E = - grad (V)
Un semiconduttore drogato è elettricamente NEUTRO. In quelli di tipo n la curva negativa dovuta agli elettroni in eccesso è bilanciata dalla carica positiva degli atomi ( ioni ) donatori. Viceversa per quelli di tipo p.
Facendo diffondere in un cristallo di semiconduttori delle impurezze di tipo p da un lato e impurezze di tipo n dall'altro, si ottiene una superficie di separazione tra la zona p e la zona n detta GIUNZIONE
A causa dell'elevatissimo gradiente di concentrazione delle cariche libere, si avrà una corrente di diffusione tra le due zone. La mancanza di lacune nella zona drogate n farà sì che queste si diffondano nella zona p. come conseguenza di tali spostamenti si avranno delle ricombinazioni: lacune con elettroni nella zona n ed elettroni nella zona p. nella zona della giunzione si determinerà un forte calo delle cariche libere (idealmente totale) a formare una REGIONE di SVUOTAMENTO (di cariche). In tale regione rimangono (idealmente) solo ioni negativi (accettori presenti nella zona p) e positivi (donatori presenti nella zona n). la regione di svuotamento (o anche ZONA di CARICA SPAZIALE) si presenta come un dielettrico fra due zone cariche, una positiva e l'altra negativa. A causa di ciò essa determina un effetto capacitivo ai capi della giunzione. Ciò implica l'esistenza di un campo elettrico. Il verso di tale campo è opposto al movimento di diffusione di cariche maggioritarie. Quella piccola parte di portatori presente ( elettroni verso la zona n; lacune verso la zona p ). Tali spostamenti (diffusione e drift) avranno luogo fin quando non si annulleranno a vicenda. In corrispondenza di tale situazione il campo elettrico interno (detto per l'appunto BUILT IN) si stabilizza ad un valore tale da creare una BARRIERA di POTENZIALE di altezza V (nell'ordine dei decimi di volt). V è detto POTENZIALE di CONTATTO. Dall'equazione del trasporto (drift-diffusion) è possibile ottenere il valore di V
Consideriamo il caso delle lacune. Si ha che: qmppdV = qDpdp(x)
dx -V pp dx
1 dV = dp
VT pn p
Gli estremi di integrazione costituiscono la concentrazione di lacune nel materiale n (pn) e la concentrazione nel materiale p (pp). Sappiamo però che su un materiale di tipo p si ha che:
pp NA, per cui è possibile dire che V = VT[ln(NA) - ln(pn)]; sapendo che n p = ni allora l'equazione diventa V = VT[ ln (NA ND)- ln (ni
Il raggiungimento di tale risultato non serve conoscere la legge di distribuzione della carica spaziale.
Altra informazione importante per ciò che concerne il diodo è la LARGHEZZA della REGIONE di SVUOTAMENTO. Chiamata con Lp la larghezza della regione di svuotamento del semiconduttore p e con Ln quella del semiconduttore n, si dimostra che:
Lp NA = Ln ND NEUTRALITÀ di CARICA
La larghezza totale sarà data da L = Lp + Ln. In particolare:
Lp = L ND e Ln = L NA .
NA+ND NA+ND
Se invece NA = ND allora si ha anche Ln = Lp
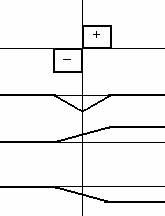 Nella vicinanza della funzione gli atomi che per ricombinazione hanno
acquisito un elettrone ( nella zona p ) divengono IONI NEGATIVI. Si avrà dunque
una certa densità di carica (positiva nella zona n, negativa nella zona p) che
dipenderà in generale dal modo in cui è drogato il diodo. Se supponiamo che
tale zona di svuotamento sia
completamente (idealmente) svuotata delle cariche mobili, si avrà una perfetta
distribuzione della carica (negativa nella zona p, positiva nella zona n) in
modo uniforme.
Nella vicinanza della funzione gli atomi che per ricombinazione hanno
acquisito un elettrone ( nella zona p ) divengono IONI NEGATIVI. Si avrà dunque
una certa densità di carica (positiva nella zona n, negativa nella zona p) che
dipenderà in generale dal modo in cui è drogato il diodo. Se supponiamo che
tale zona di svuotamento sia
completamente (idealmente) svuotata delle cariche mobili, si avrà una perfetta
distribuzione della carica (negativa nella zona p, positiva nella zona n) in
modo uniforme.
Nella zona p si ha r = -qNA
Nella zona n si ha r = qND
È ora possibile calcolare il campo
di BUILT-IN E = -qNDLn = -qNALp
e e
È anche possibile calcolarsi l'andamento del campo di BUILT-IN tramite: V(x) = E(x)dx
La LARGHEZZA della ZONA di SVUOTAMENTO è data dalla relazione:
L = [2eV (NA + ND
q
Applicando una batteria ai capi di un cristallo di un semiconduttore pn si hanno risultati diversi a seconda del tipo di polarizzazione e della tensione della batteria.
Con la POLARIZZAZIONE DIRETTA il polo positivo della batteria è collegato alla zona p e il negativo alla zona n. Tale situazione farà comparire nuove lacune nella zona p e nuovi elettroni nella zona n. In tal modo verrà incentivata la diffusione di cariche maggioritarie, poiché la zona di carica spaziale si sarà ridotta: in tal modo la barriera di potenziale da V passerà a VJ = V - V dove V è la tensione della batteria. In tal modo le cariche si diffonderanno più facilmente.
Con la POLARIZZAZIONE INVERSA il polo positivo della batteria è collegato alla zona n e il negativo alla zona p. Tale situazione farà diminuire il numero di elettroni e lacune rispettivamente nella zona n e nella zona p. Questo a vantaggio dell'estensione della zona di svuotamento, con conseguente aumento della barriera di potenziale che passerà da V a VJ = V + V dove V è la tensione della batteria. Con ciò i portatori di carica maggioritaria saranno ulteriormente "frenati" nella diffusione, mentre la pur piccolissima quantità di cariche minoritarie sarà incentivata a derivare da una parte all'altra della giunzione. Com'è facilmente intuibile la corrente per il caso della P.D. è diretta da p a n, mentre nel caso della P.I. la corrente scorre da n a p ( CORRENTE INVERSA di SATURAZIONE
Il dispositivo a semiconduttore composto da una giunzione p|n è detto DIODO
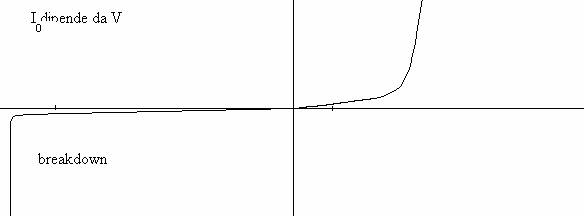
Considerando l'espressione generale della CORRENTE nel DIODO : I = I (e V/2VT-1); in essa si possono notare la dipendenza esponenziale della tensione V applicata dalla VT (che è l'equivalente in tensione della temperatura : VT = T/11600) e da hche varia a seconda del materiale e delle correnti (h = 1 per il Ge; h @ 2 per il Si in caso delle basse correnti, h 1 per il Si in caso di correnti elevate); si nota inoltre la dipendenza di I da I (corrente di saturazione inversa).
 I
I
I
Vg V
Spostandosi da destra verso sinistra del grafico lungo l'asse delle V si passa da regime di polarizzazione inversa a regime di polarizzazione diretta.
Si nota una forte corrente negativa (che pregiudica l'integrità del diodo) in corrispondenza di una tensione negativa particolarmente elevata: tale fenomeno è detto BREAKDOWN. Per moduli della tensione minori la corrente del diodo vale I -I . tale valore è però direttamente dipendente dalla temperatura. All'aumentare della temperatura abbiamo un incremento di I . In modo approssimativo si può dire che essa raddoppia per ogni aumento di temperatura di 10°C. per voler mantenere un valore costante di I al variare di T si può agire su V. Per avere I =cost deve essere: dV -2.5mV dT °C
Scorrendo il grafico si trova che per V = 0, I = 0. tale relazione è quella allo stato di equilibrio. Di seguito la V cresce, ma non ci sono variazioni significative di corrente. Arrivati ad una tensione Vg detta TENSIONE di SOGLIA (o di OFFSET) la corrente I è apprezzabile. Aumentando leggermente V si ha una notevole crescita di I. in particolare l'andamento di I(V) diviene esponenziale. A causa di ciò è possibile dire (regime di conduzione) che I I e V/hVT essendo la corrente I0 ad essa sottratta molto piccola ( nell'ordine dei nA ). In questo caso la dipendenza di I dalla T è trascurabile rispetto a quella della V. il diodo ha una sua resistenza interna che può essere vista sotto l'aspetto STATICO o sotto l'aspetto DINAMICO. La RESISTENZA STATICA è definita come R = V/I ma essa è praticamente inutile. Questo perché il diodo è usato con segnali reversibili più o meno nel tempo. Nel caso di segnali con leggeri spostamenti si considera la RESISTENZA DINAMICA del diodo:
Rd hVT/I che in tal caso può essere considerata costante.
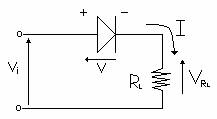 Considerando ora un circuito di tensione nel diodo e una RL posti in serie possiamo dire che la caduta di tensione nel diodo è
Considerando ora un circuito di tensione nel diodo e una RL posti in serie possiamo dire che la caduta di tensione nel diodo è
V = Vi - VRL la quale rappresenta la RETTA di CARICO del circuito, avente pendenza -1/RL. Tale equazione non è però sufficiente per determinare V e I. ci viene in aiuto la caratteristica statica del diodo. L'intersezione tra l'ultima e la retta di carico fornisce i valori di I e V per quel particolare diodo, in quel circuito con quel valore di RL avendo in ingresso una tensione Vi: viene cioè individuato il PUNTO di LAVORO (Q).
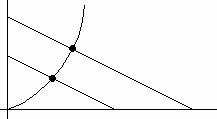 Fin quando il segnale di ingresso ha piccoli scostamenti, il punto Q si
sposta in modo non eccessivo: in tal modo è possibile approssimare Rd come una costante. Se invece Vi compie ampie escursioni
è possibile (escludendo la zona di breakdown) rappresentare il diodo con un
modello circuitale che assume due forme:
Fin quando il segnale di ingresso ha piccoli scostamenti, il punto Q si
sposta in modo non eccessivo: in tal modo è possibile approssimare Rd come una costante. Se invece Vi compie ampie escursioni
è possibile (escludendo la zona di breakdown) rappresentare il diodo con un
modello circuitale che assume due forme:
in polarizzazione diretta per V > Vg si può considerare il diodo come un generatore di tensione di valore Vg con in serie una resistenza molto piccola (idealmente la resistenza è un corto circuito) e conseguente caratteristica con una grandissima pendenza 1/R (idealmente una retta verticale);
in polarizzazione inversa si può considerare il diodo come una resistenza elevatissima ( idealmente è un circuito aperto) e conseguentemente la retta ha pendenza bassissima 1/R (idealmente è verticale).
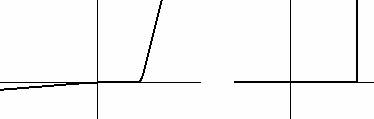
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026