SDOPPIAMENTO DEI LIVELLI ENERGETICI RELATIVI ALL'ACCOSTAMENTO DI DUE BUCHE DI POTENZIALE

tecnica

Sdoppiamento dei livelli energetici relativi all'accostamento  di due buche di potenziale

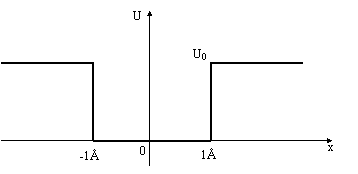
Consideriamo un potenziale a buca centrato nell'origine di altezza U₀ = 60eV:

Risolvendo l'eq. di Schrödinger si ottengono tre possibili autofunzioni dell' 525f55f energia; due simmetriche e una antisimmetrica (alternate tra loro per energie crescenti a partire da quella simmetrica), di energie:

E₁=5,95 eV E₂=23,24 eV E₃=48,96 eV

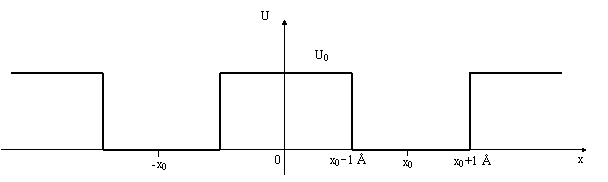
Se andiamo invece a considerare il caso di due buche identiche disposte simmetricamente rispetto all'origine, cioè con i centri in x₀ e -x₀, sempre con la stessa larghezza e profondità:

Se risolviamo l'equazione di Schrödinger separatamente nel caso di soluzioni simmetriche e antisimmetriche imponendo le condizioni di raccordo per le y(x) e le loro derivate ai bordi delle buche, otteniamo che per avere soluzioni non nulle per le y, l'energia dovrà soddisfare le seguenti equazioni (rispettivamente col per le y simmetriche e col + per le antisimmetriche):

Con w = ,   b =  , a = 1 Å , m = m_e = 9,11 10^-31 Kg

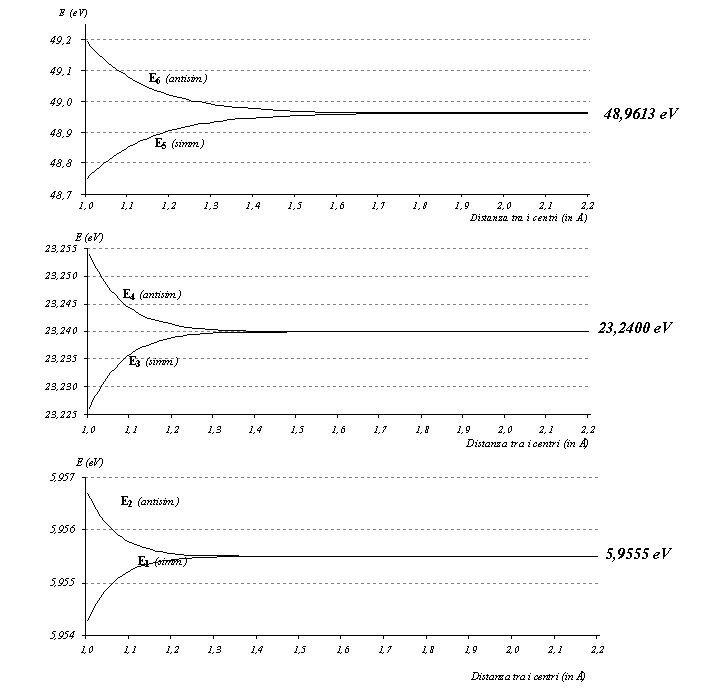
Dalle soluzioni di queste equazioni, al variare del parametro x₀ , si ottengono 6 livelli energetici accoppiati a due a due, nel senso che a due a due hanno valori molto vicini di energia. Già per valori di x₀ superiori a 1,8 Å, quindi per distanze buca buca superiori a 1,6 Å si osserva che i livelli praticamente si sovrappongono a due a due, in quanto le differenze energetiche sono estremamente piccole.

Per esempio per x₀ = 1,8 Å le differenze di energie sono:

E₂ E₁ = 0,0000000146 eV

E₄ E₃ = 0,00000134 eV

E₆ E₅ = 0,00191 eV

A tali distanze quindi è come se le due buche fossero indipendenti, infatti osserviamo che si riottengono proprio i 3 livelli energetici calcolati per la singola buca.

		Emanuele Iannone 28 mar '99