Teorema della divergenza

matematica

Teorema della divergenza

Sia Y euclideo orientato, G aperto limitato stokiano di Y, campo su un aperto di Y contenente .

Allora:

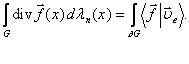
In realtà dimostreremo la seguente versione più g 525i82f enerale:

Sia Y euclideo orientato, G aperto stokiano, campo a supporto compatto in Y. Allora:

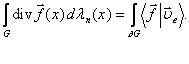
Dim: Usiamo il seguente risultato:

Lemma

Sia V= , cubo aperto. Sia inoltre di classe , con

Sia funzione con supporto compatto contenuto in V. Allora:

Sia poi   e

Posto e 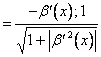, si ha:

Dim: Non è restrittivo supporre . Usando la formula di riduzione, (considerando j=x) si ha:

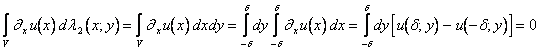
essendo poiché supp e quindi u è nulla su

Per quanto riguarda la seconda parte del Teorema:

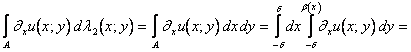
conoscendo la formula di derivazione per integrali dipendenti da parametro,

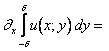
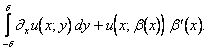
si ottiene

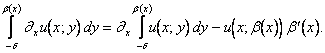
Ritornando al problema principale,

.

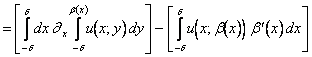Detti (A) e (B) i due termini scritti qui sopra, studiamo (A): posto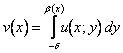

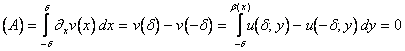
essendo appunto supp e quindi u è nulla su. Per quanto riguarda (B),

=

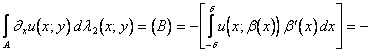
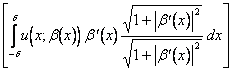Se invece ho:

=   (***)

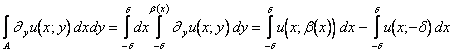considerando che

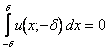
si ha:

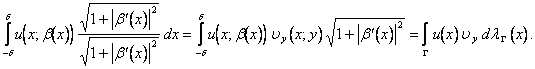(***) =   CVD

Ritornando alla dimostrazione del teorema della divergenza, consideriamo il

Lemma (delle partizioni dell'unità):

Sia una famiglia di aperti di Y (euclideo). Esiste allora una successione di funzioni positive

e tali che, posto ,

1) supp è compatto, ed è contenuto in , per qualche

la famiglia supp è localmente finita in : cioè, per ogni punto , esiste un intorno di y, tale chesupp solo per un insieme finito di indici ;

.

Ogni tale successione di funzioni è detta partizione dell'unità subordinata al ricoprimento aperto

Dimostriamo il teorema della divergenza solo nel caso di frontiera regolare, \.

Si ponga compatto. Allora se , consideriamo il cubetto . Allora è tale che

partizione dell'unità; quindi valgono le proprietà 1),2),3) del lemma delle partizioni.

In particolare per la 3), , quindi .

Posso applicare il lemma iniziale a ciascun , ovvero

.

Poiché in (e quindi a maggior ragione in ) si ha , allora:

CVD