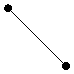
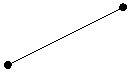
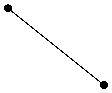
Utilizzando spline del primo ordine, per m=1 otteniamo segmenti di retta, cioè nei nodi sono presenti punti angolosi. In altre parole la funzione approssimatrice non è <<regolare>> nei nodi perché la derivata prima non è continua, perciò il loro impiego risulta limitato.

L'espressione generale di queste funzioni è:

f(x)=f(x_i)+m_i(x-x_i)

Grafico della funzione

f(x)

Spline del 1° Ordine

2

0 x

Secondo Ordine:

- Se invece utilizziamo spline del secondo ordine, per m=2, otteniamo segmenti di parabola. L'espressione generale di queste funzioni è:

f_i(x)=a_ix²+b_ix+c_i

Per n+1 punti base vi sono n intervalli, pertanto bisogna determinare tre n costanti per tre n condizioni, o equazioni.

1° condizione

I valori delle curve spline devono essere uguali in corrispondenza dei nodi interni:

a_i-1 X_i-1² + b_i-1-1X_i-1 + c_i-1=f(x_i-1)

a_i-1 X_i-1²+ b_i-1X_i-1 + c =f(x_i-1)    per i=1,2,..,n

2° condizione

La prima e l'ultima curva spline devono passare per i corrispondenti punti esterni:

a₁ X₀²+ b₁X₀ + c₁ =f(x₀)

a_N X_N²+ b_N X_N + c_N =f(x_N)

3° condizione

Le derivate prime delle coppie di spline adiacenti devono essere uguali nei nodi:

2a_i-1 X_i + b_i-1=2a_i X_i + b_i    per i=2,..,n

4° condizione

La derivata seconda è nulla in corrispondenza del punto X₀ cioè a₁=0.

Otterremo la soluzione dell'interpolazione risolvendo il sistema un sistema lineare 3n*3n; una volta risolto il sistema, notaremo due aspetti negativi:

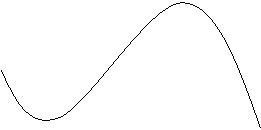
i primi due punti sono uniti da una retta e l'ultima spline tende verso l'alto. Per questo motivo le spline del secondo ordine non hanno molta importanza.

Spline del 2° Ordine

f(x)

2

x

0

Terzo Ordine:

- Le Curve spline del terzo ordine, dette anche cubiche naturali, sono quelle che più ci interesano, che collegano i nodi delimitanti ogni intervallo con una funzione polinomiale del terzo ordine del tipo:

f_i(X)=a_iX3+b₁X²+c_iX+d_i con X_i-1<=X<X_i

Come per le spline quadratiche il calcolo delle incognite richiede cinque condizioni; le condizioni 1, 2 e 3 che abbiamo visto nelle spline quadratiche devono essere soddisfatte anche in quelle cubiche e inoltre per le condizioni di raccordo le spline adiacenti nei punti comuni devono avere non solo la stessa tangente, ma anche la stessa curvatura, cioè le derivate seconda delle spline adiacenti devono essere uguali in corrispondenza dei nodi comuni. Infine imporremo le condizioni affinchè la Spline degli estremi sia una retta o sia una <<spline naturale>>.

Così le condizioni I°,II°,III°,IV°,V° in totale daranno:

2(n-1)+ 2 + (n-1) + (n-1) + 2= 4n

equazioni indipendenti sufficienti per determinare i 4n coefficienti degli n polinomi di terzo grado.

Il sistema lineare 4n*4n ha una e solo una soluzione e permette di ottenere le spline richieste.

Ma noi per ovviare questo problema seguiremo un altro procedimento, il quale richiede la soluzione di un sistema di solo n-1 equazioni.

f(x)

Spline Cubica

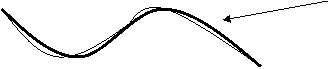
Polinomiale Cubica Interpolante

x

0

Nell'analisi numerica le funzioni Spline, oltre che nell' interpolazione,  sono anche usate nella risoluzione di problemi al limite per equazioni ordinarie o alle derivate parziali.