|
|
| |
Posizioni di una Retta su un piano cartesiano.
Modello ![]() e finalità
applicative.
e finalità
applicative.
Il Limite di un numero: i 4 casi.
Teoremi ed Operazioni sui Limiti.
Funzione Esponenziale e Logaritmica.
Risoluzione approssimata d'equazioni trascendenti ed algebriche.
Che cos'è un'equazione differenziale? E perché le abbiamo introdotte?
Esiste una formula di risoluzione dell'equazione differenziale?
Come si risolve un'equazione differenziale lineare non omogenea?
Che cosa sono gli integrali impropri?
Come si risolve un'equazione differenziale lineare non omogenea del 2° ordine?
Teorema di Lagrange o del valor medio.
Teorema d'esistenza della radice.
Teoremi d'unicità della soluzione.
Criterio Del Confronto O Di D'Alambert.
Criterio Della Radice O Di Cauchy.
Quali sono i teoremi applicabili ad una serie uniformemente convergente?
Continuità Della Somma D'Una Serie.
 Il luogo geometrico è
fondamentale per l'algebra. Infatti il luogo geometrico è l'insieme dei punti
che hanno una stessa caratteristica. Prendiamo gli assi cartesiani: dalla definizione
di luogo siamo partiti per trovare il modello matematico di una retta passante
per il punto di ordinata h. La retta y=h è per definizione il luogo di tutti i
punti che hanno ordinata uguale ad h.
Il luogo geometrico è
fondamentale per l'algebra. Infatti il luogo geometrico è l'insieme dei punti
che hanno una stessa caratteristica. Prendiamo gli assi cartesiani: dalla definizione
di luogo siamo partiti per trovare il modello matematico di una retta passante
per il punto di ordinata h. La retta y=h è per definizione il luogo di tutti i
punti che hanno ordinata uguale ad h.
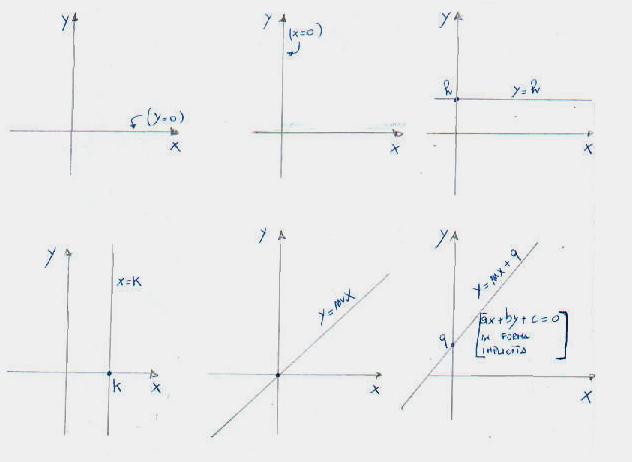
Le possibili posizioni di una retta sono sei. Per trovare i rispettivi modelli matematici siamo partiti dal concetto di luogo geometrico (come visto sopra). Infatti il luogo geometrico, per definizione, è un insieme di punti che hanno una stessa caratteristica in comune. Per esempio prendiamo l'asse delle x è y=0, ogni punto che prendiamo sull'asse delle ascisse, ha l'ordinata sempre zero. La retta delle ascisse, quindi, è il luogo dei punti del piano cartesiano che hanno ordinata nulla (0). La figura rappresenta le sei posizione di una retta nel piano cartesiano.
Un sistema lineare è formato da due equazioni in due incognite ed è di
primo grado. Ha forma del tipo: ![]() . La soluzione è una coppia di numeri che soddisfa contemporaneamente
le due equazioni; interpretando le due equazioni del sistema lineare come due
rette del piano, la soluzione rappresenta l'eventuale punto di incontro tra le
due rette. Infatti, due rette del piano possono anche non incontrarsi.
. La soluzione è una coppia di numeri che soddisfa contemporaneamente
le due equazioni; interpretando le due equazioni del sistema lineare come due
rette del piano, la soluzione rappresenta l'eventuale punto di incontro tra le
due rette. Infatti, due rette del piano possono anche non incontrarsi.
Esistono più metodi per risolvere un sistema.Il metodo più rapido è
quello di Kramer. Questo metodo si riferisce all'interpretazione geometrica del
sistema; infatti calcolando il determinante (![]() ) si hanno vari casi:D>0 le rette sono incidenti (sistema
determinato); D=0 le rette sono parallele(sistema impossibile); D<0 le
rette sono coincidenti (sistema indeterminato). Anche analizzando le due
equazioni ci possiamo accorgere d'alcune cose. Se il rapporto a/a' è diverso
dal rapporto b/b' le due rette sono incidenti; con
) si hanno vari casi:D>0 le rette sono incidenti (sistema
determinato); D=0 le rette sono parallele(sistema impossibile); D<0 le
rette sono coincidenti (sistema indeterminato). Anche analizzando le due
equazioni ci possiamo accorgere d'alcune cose. Se il rapporto a/a' è diverso
dal rapporto b/b' le due rette sono incidenti; con ![]() le due rette sono parallele; se i rapporti tra i coefficienti
sono tutti uguali(
le due rette sono parallele; se i rapporti tra i coefficienti
sono tutti uguali(![]() ) allora le due rette sono coincidenti. Gli altri metodi di
risoluzione dei sistemi lineari sono: riduzione, confronto e sostituzione;
questi hanno in comune lo scopo di eliminare una variabile.
) allora le due rette sono coincidenti. Gli altri metodi di
risoluzione dei sistemi lineari sono: riduzione, confronto e sostituzione;
questi hanno in comune lo scopo di eliminare una variabile.
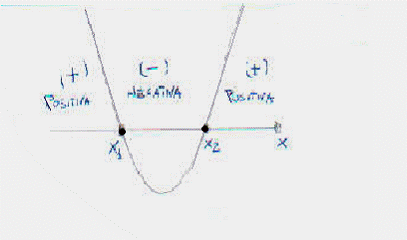 Una disequazione di 2° grado
Una disequazione di 2° grado ![]() si può ricondurre ad una curva del 2° ordine, per l'esattezza
ad una parabola. Infatti ponendo la disequazione come equazione di una parabola,
si può ricondurre ad una curva del 2° ordine, per l'esattezza
ad una parabola. Infatti ponendo la disequazione come equazione di una parabola,![]() , forse riesco ad ottenere alcune informazioni su questa
disequazione. Metto successivamente l'equazione
, forse riesco ad ottenere alcune informazioni su questa
disequazione. Metto successivamente l'equazione ![]() a sistema con
l'equazione rappresentativa delle ascisse y
a sistema con
l'equazione rappresentativa delle ascisse y
=0 , ed avrò una equazione di 2° grado in x che risolvo con la formula: ![]() . Trovate le due/una soluzione/i, le analizzo graficamente.
(infatti potrà accadere che con
. Trovate le due/una soluzione/i, le analizzo graficamente.
(infatti potrà accadere che con ![]() non si hanno soluzione
nel campo dei reali; con
non si hanno soluzione
nel campo dei reali; con ![]() avremo due soluzioni
reali e coincidenti;
avremo due soluzioni
reali e coincidenti; ![]() otterremo le due
soluzioni reali e distinte). Vediamo per esempio la figura qui sotto.
Ricordando che la parabola avrà concavità verso l'alto se a>0, concavità
verso il basso se a<0. La figura riporta l'esempio di una parabola con
a>0, e due 434i86e soluzioni reali e distinte. In questo caso avremo che la
disequazione è verificata
otterremo le due
soluzioni reali e distinte). Vediamo per esempio la figura qui sotto.
Ricordando che la parabola avrà concavità verso l'alto se a>0, concavità
verso il basso se a<0. La figura riporta l'esempio di una parabola con
a>0, e due 434i86e soluzioni reali e distinte. In questo caso avremo che la
disequazione è verificata ![]() se era
se era ![]() , mentre era verificata per
, mentre era verificata per ![]() se le disequazione di
partenza era
se le disequazione di
partenza era ![]() .
.
![]() è l'equazione di una conica di 2° grado. La circonferenza è
il luogo geometrico dei punti che è equidistante da un punto fissato detto
centro. I coefficienti delle x2, y2 devono essere uguali,
inoltre per dire che l'equazione di secondo grado in x e y rappresenti una
circonferenza nel piano, deve mancare il termine misto. Altra condizione per risultare
che l'equazione sia una circonferenza è che sia verificata la condizione di
realtà del raggio:
è l'equazione di una conica di 2° grado. La circonferenza è
il luogo geometrico dei punti che è equidistante da un punto fissato detto
centro. I coefficienti delle x2, y2 devono essere uguali,
inoltre per dire che l'equazione di secondo grado in x e y rappresenti una
circonferenza nel piano, deve mancare il termine misto. Altra condizione per risultare
che l'equazione sia una circonferenza è che sia verificata la condizione di
realtà del raggio: ![]() . La realtà del raggio
deve essere maggiore di zero, infatti se è u
. La realtà del raggio
deve essere maggiore di zero, infatti se è u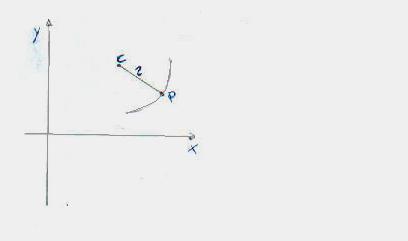 guale a zero la circonferenza
degenera in un punto e se è minore di zero la circonferenza è impossibile. C'è
un equazione cartesiana che ci fornisce subito il raggio
guale a zero la circonferenza
degenera in un punto e se è minore di zero la circonferenza è impossibile. C'è
un equazione cartesiana che ci fornisce subito il raggio ![]() , dove
, dove ![]() sono le coordinate del
centro. Per risalire alla formula abbiamo utilizzato il luogo geometrico. CP lo
poniamo uguale al raggio quindi avrò
sono le coordinate del
centro. Per risalire alla formula abbiamo utilizzato il luogo geometrico. CP lo
poniamo uguale al raggio quindi avrò ![]() elevando al quadrato
che
elevando al quadrato
che ![]() , quindi con
, quindi con ![]() e svolgendo i quadrati ho:
e svolgendo i quadrati ho: ![]() . Ponendo
. Ponendo ![]() , ottengo la formula vista in partenza.
, ottengo la formula vista in partenza. ![]() . Le coordinate del centro della circonferenza sono:
. Le coordinate del centro della circonferenza sono: ![]() .
.
La funzione è una applicazione di due insiemi X e Y non vuoti. Essa è una relazione che ad ogni xiX fa corrispondere uno ed un solo yiY. L'insieme X è il dominio dell'applicazione, mentre l'insieme Y si chiama condominio o insieme delle immagini. Le funzioni possono essere algebriche e trascendenti. A sua volta le funzioni algebriche si dividono in: funzioni razionali intere, quando le operazioni su x siano addizioni, sottrazioni, moltiplicazioni ed elevamento a potenza con esponente intero positivo; funzioni razionali fratte, quando in aggiunta vi è anche l'operazione di divisione; funzioni irrazionali, quando compaiono estrazioni di radice n-esima. Le funzioni trascendenti sono quelle che non sono algebriche; tra esse vi sono le funzioni goniometriche e loro inverse, le funzioni esponenziali e logaritmiche.
Si chiama intorno completo di un numero reale c un qualsiasi intervallo
al quale appartenga c come elemento interno. In generale per intorno completo
di c si intende l'intervallo ![]() , con
, con ![]() numeri positivi. Si definisce l'interno sinistro del numero
reale c l'insieme di tutti i numeri di un intervallo aperto avente c
com'esterno destro.
numeri positivi. Si definisce l'interno sinistro del numero
reale c l'insieme di tutti i numeri di un intervallo aperto avente c
com'esterno destro.
![]() . La scrittura, riportata di fianco, ha un significato ben
preciso; la verifica della stessa richiede l'esame della disequazione in modulo
. La scrittura, riportata di fianco, ha un significato ben
preciso; la verifica della stessa richiede l'esame della disequazione in modulo
![]() ; che se soddisfatta per un intorno effettivo del punto c
dell'insieme di esistenza della funzione in esame prova l'esattezza della
scrittura di partenza.
; che se soddisfatta per un intorno effettivo del punto c
dell'insieme di esistenza della funzione in esame prova l'esattezza della
scrittura di partenza.
La scrittura ![]() ottenuta attraverso
l'esame di un tabulato segue la disequazione in modulo
ottenuta attraverso
l'esame di un tabulato segue la disequazione in modulo ![]() , che se soddisfatta per un intorno effettivo del punto c in
cui la funzione perde di significato trova l'esattezza della scrittura di
partenza. Quindi se
, che se soddisfatta per un intorno effettivo del punto c in
cui la funzione perde di significato trova l'esattezza della scrittura di
partenza. Quindi se ![]() allora
allora![]() , se
, se ![]() allora
allora ![]() .
.
Per ![]() si deve verificare che la disequazione in modulo
si deve verificare che la disequazione in modulo ![]() ; sia soddisfatta solo da valori facenti parte dell'intorno
completo dell'infinito.
; sia soddisfatta solo da valori facenti parte dell'intorno
completo dell'infinito.
La scrittura ![]() ha senso di esser
scritta quando la disequazione
ha senso di esser
scritta quando la disequazione ![]() è verificata nell'intorno completo dell'infinito con M
positivo e arbitrariamente grande.
è verificata nell'intorno completo dell'infinito con M
positivo e arbitrariamente grande.
Se una funzione f(x) ammette il limite finito l, allora la funzione -f(x) ammette il limite -l.
Se la funzione ha per limite l, la funzione f(x)-A ha per limite l-A.
Se, per x c, la funzione f(x) ammette un limite, questo è unico.
Se, per x c, la funzione f(x) tende al limite finito l diverso da zero, esiste un intorno di c per tutti i punti del quale, escluso al più c, i valori della funzione hanno lo stesso segno del limite.
Se in un intorno del punto c, escluso al più x=c, la funzione f(x) è positiva o nulla ed ammette limite l per x c, allora lS
Se in un intorno del punto c, escluso al più x=c, la funzione f(x) è negativa o nulla ed ammette limite l per x c, allora lR
Se due funzioni g(x) e (x)
tendono allo stesso limite l per x c ed una terza funzione f(x) è tale che, in un certo intorno di c,
escluso al più c, si abbia g(x) Rf(x) R (x) allora
è anche ![]() .
.
Se due funzioni f(x) e g(x) sono tali che |f(x)| R|g(x)| per tutti gli x di un intorno di C e se g(x) 0 per x c, allora anche f(x) 0 per x c.
Se f(x) e g(x) sono due funzioni
che in un intorno ci c soddisfano la condizione |f(x)| S|g(x)|e se
inoltre ![]() , allora risulta
, allora risulta ![]() .
.
Se per x c la
funzione f(x) tende al limite finito l, allora ![]() , ossia il limite del modulo di una funzione è il modulo del
limite.
, ossia il limite del modulo di una funzione è il modulo del
limite.
Il limite della somma di due
funzioni è uguale alla somma dei limiti. ![]() .
.
La differenza di due funzioni ha per limite la differenza dei limiti.
Il limite della somma algebrica di più funzioni è uguale alla somma algebrica dei limiti delle singole funzioni.
Il limite del prodotto di una
costante per una funzione è uguale al prodotto della costante per il limite
della funzione. ![]() .
.
Il limite del prodotto di due
funzioni è uguale al prodotto dei limiti delle due funzioni: ![]() .
.
Il limite della potenza, con
esponente n intero positivo di una funzione che tende a un limite finito è la
potenza n-esima del limite : ![]() .
.
Se, per x c, f(x)
tende al limite finito l diverso da zero, la funzione inversa , ![]() , tende sempre per x c, al limite 1/l.
, tende sempre per x c, al limite 1/l.
Quando la funzione f(x) tende a
zero, la funzione ![]() tende all'infinito.
tende all'infinito.
Quando la funzione f(x) tende
all'infinito , la funzione ![]() tende allo zero.
tende allo zero.
Il limite del quoziente di due
funzioni, la seconda delle quali tenda ad un limite finito diverso da zero, è
uguale al quoziente dei limiti. ![]() .
.
Se f(x) tende al limite l ed è
l>0, allora ![]() ; se lR0 vale solo se n è dispari.
; se lR0 vale solo se n è dispari.
![]() . Nella scrittura riportata di fianco va tolta ogni forma di
indecisione del tipo
. Nella scrittura riportata di fianco va tolta ogni forma di
indecisione del tipo ![]() oppure
oppure ![]() , e così via. Per fare ciò bisogna mettere in evidenza la x,
al massimo grado, sia al numeratore che al denominatore. Applicando i vari teoremi
visti in precedenza, avremo che la scrittura di partenza si riduce al semplice studio del limite:
, e così via. Per fare ciò bisogna mettere in evidenza la x,
al massimo grado, sia al numeratore che al denominatore. Applicando i vari teoremi
visti in precedenza, avremo che la scrittura di partenza si riduce al semplice studio del limite: ![]() . Si avranno tre casi allora:
. Si avranno tre casi allora:
Con m>n ![]() ; mentre
; mentre ![]() sarà uguale a
sarà uguale a ![]() se m-n è dispari,
se m-n è dispari, ![]() se m-n è pari.
se m-n è pari.
Con m=n ![]() .
.
Con m<n ![]()
![]() . Dalla trigonometria si ha che:
. Dalla trigonometria si ha che: ![]() , rapportato ai limiti si ha:
, rapportato ai limiti si ha: ![]() . Siccome
. Siccome ![]() , con x=0, tutto si riduce a:
, con x=0, tutto si riduce a: ![]() .
.
Il rapporto tra il seno di un arco
e l'arco stesso, espresso in radianti, tende ad 1, quando l'arco tende a zero,
cioè ![]() .
.
![]() , ha insieme di esistenza
, ha insieme di esistenza ![]() . Si dimostra che la funzione sopraindicata ha per limite,
per
. Si dimostra che la funzione sopraindicata ha per limite,
per ![]() un numero irrazionale
trascendente che si suole indicare con la lettera e, quindi
un numero irrazionale
trascendente che si suole indicare con la lettera e, quindi ![]() .
.
I limiti di una somma, di un prodotto e di un quoziente, perdono
validità quando il limite dato si presenta sotto una delle seguenti forme: ![]() . Queste si dicono forme indeterminate o di indecisione in
quanto in questi casi, non si può dire subito se esiste il limite e quale ne
sia il valore.
. Queste si dicono forme indeterminate o di indecisione in
quanto in questi casi, non si può dire subito se esiste il limite e quale ne
sia il valore.
Quando l'indeterminata x appare sotto il segno di radice la
disequazione dicesi irrazionale. Una disequazione di tal genere può essere
ridotta a una delle seguenti formule dette canoniche 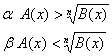 , dove bisogna distinguere due casi fondamentali a seconda
dell'indice del radicale n, a seconda che sia intero dispari o intero pari. Se
n è un intero dispari la risoluzione non presenta nessuna difficoltà, non
essendoci limitazioni all'esistenza di radicali per n dispari; basterà, dopo
aver elevato a potenza ambo i membri per l'ennesima potenza, risolvere la
disuguaglianza irrazionale che seguirà. Se invece n è un radicale pari
bisognerà distinguere due casi:
, dove bisogna distinguere due casi fondamentali a seconda
dell'indice del radicale n, a seconda che sia intero dispari o intero pari. Se
n è un intero dispari la risoluzione non presenta nessuna difficoltà, non
essendoci limitazioni all'esistenza di radicali per n dispari; basterà, dopo
aver elevato a potenza ambo i membri per l'ennesima potenza, risolvere la
disuguaglianza irrazionale che seguirà. Se invece n è un radicale pari
bisognerà distinguere due casi:
I)
![]() . Questa disequazione irrazionale può essere risolta,
mettendo a sistema le tre disequazioni:
. Questa disequazione irrazionale può essere risolta,
mettendo a sistema le tre disequazioni: ![]() ; che derivano dalle seguenti considerazioni. Perché il radicale
esista deve essere B(x) maggiore o uguale a zero, da cui segue che A(x) deve
essere maggiore di zero. Con queste due posizioni diciamo che i due membri
siano positivi. Imponendo che la potenza ennesima del primo membro sia maggiore
della potenza del secondo concludiamo che
; che derivano dalle seguenti considerazioni. Perché il radicale
esista deve essere B(x) maggiore o uguale a zero, da cui segue che A(x) deve
essere maggiore di zero. Con queste due posizioni diciamo che i due membri
siano positivi. Imponendo che la potenza ennesima del primo membro sia maggiore
della potenza del secondo concludiamo che ![]() deve essere maggiore di
deve essere maggiore di ![]() .
.
II)
![]() . In questo caso la soluzione è data dall'unione dell'insieme
soluzione dato dai due sistemi:
. In questo caso la soluzione è data dall'unione dell'insieme
soluzione dato dai due sistemi: 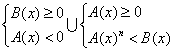 . Nel 1° sistema la prima disequazione esprime la realtà del
radicale, la seconda esprime la condizione che la disequazione data è verificata
per A(x)<0;nel secondo sistema la prima disequazione esprime il fatto che è
anche verificata per valori non negativi di A(x) a condizione che sia
verificata la disequazione razionale ottenuta elevando i due membri a potenza.
. Nel 1° sistema la prima disequazione esprime la realtà del
radicale, la seconda esprime la condizione che la disequazione data è verificata
per A(x)<0;nel secondo sistema la prima disequazione esprime il fatto che è
anche verificata per valori non negativi di A(x) a condizione che sia
verificata la disequazione razionale ottenuta elevando i due membri a potenza.
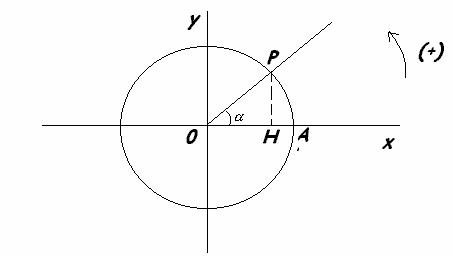 Definiamo cosa è una
circonferenza goniometrica: è una circonferenza avente per raggio l'unità di
misura e avente il centro nell'origine degli assi (quindi OA=1). Le coordinate
del punto P sono:
Definiamo cosa è una
circonferenza goniometrica: è una circonferenza avente per raggio l'unità di
misura e avente il centro nell'origine degli assi (quindi OA=1). Le coordinate
del punto P sono: 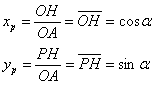 .
.
 Definiamo allora cosa sono il
coseno e il seno di un angolo. Il seno di una angolo è l'ordinata dell'estremo
dell'arco corrispondente nella circonferenza goniometrica. Il coseno è
l'ascissa dell'estremo dell'arco corrispondente nella circonferenza
goniometrica. Studiamo ora le due funzioni separatamente.
Definiamo allora cosa sono il
coseno e il seno di un angolo. Il seno di una angolo è l'ordinata dell'estremo
dell'arco corrispondente nella circonferenza goniometrica. Il coseno è
l'ascissa dell'estremo dell'arco corrispondente nella circonferenza
goniometrica. Studiamo ora le due funzioni separatamente.
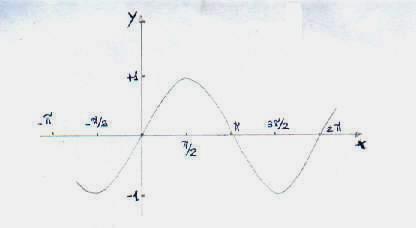
Il seno. La funzione seno è una funzione
periodica limitata continua. Limitata perché il seno è compreso tra -1 e 1. ![]() . Periodica perché dopo il periodo principale (2 oppure
360°) i valori della funzione si ripetono; quindi siamo autorizzati a scrivere
. Periodica perché dopo il periodo principale (2 oppure
360°) i valori della funzione si ripetono; quindi siamo autorizzati a scrivere ![]() . Inoltre è simmetrica rispetto all'origine (funzione
dispari). La figura riportata di fianco rappresenta il seno. Il coseno. La
. Inoltre è simmetrica rispetto all'origine (funzione
dispari). La figura riportata di fianco rappresenta il seno. Il coseno. La
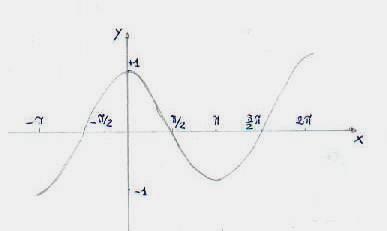 funzione coseno anch'essa ha
le stesse caratteristiche del seno, quindi possiamo scrivere
funzione coseno anch'essa ha
le stesse caratteristiche del seno, quindi possiamo scrivere ![]() . L'unica differenza sta nel fatto che la funzione coseno è
simmetrica rispetto all'asse y
. L'unica differenza sta nel fatto che la funzione coseno è
simmetrica rispetto all'asse y 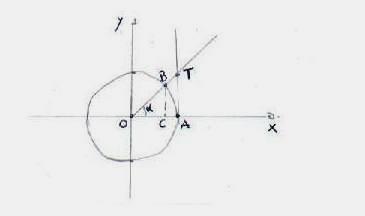 (funzione pari). La figura
riportata di fianco rappresenta il coseno. La tangente. La tangente di
un arco circolare è l'ordinata del punto d'incontro della tangente geometrica,
condotta nell'origine dell'arco alla circonferenza a cui esso appartiene, col
prolungamento del raggio passante
(funzione pari). La figura
riportata di fianco rappresenta il coseno. La tangente. La tangente di
un arco circolare è l'ordinata del punto d'incontro della tangente geometrica,
condotta nell'origine dell'arco alla circonferenza a cui esso appartiene, col
prolungamento del raggio passante ![]() . Possiamo osservare che dopo (180°) si
ripropongono gli stessi valori; quindi il periodo
. Possiamo osservare che dopo (180°) si
ripropongono gli stessi valori; quindi il periodo 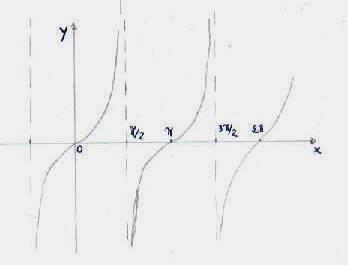 della tangente, anch'essa
funzione periodica, è . Si può dire che
della tangente, anch'essa
funzione periodica, è . Si può dire che ![]() . La funzione tangente è simmetrica rispetto all'origine
(funzione dispari). Esistono alcune relazioni fondamentali tra le tre funzioni
trigonometriche. Per il criterio di similitudine dei triangoli ottengo: AT : CB
= 1 : OC , e cioè
. La funzione tangente è simmetrica rispetto all'origine
(funzione dispari). Esistono alcune relazioni fondamentali tra le tre funzioni
trigonometriche. Per il criterio di similitudine dei triangoli ottengo: AT : CB
= 1 : OC , e cioè ![]() . Per il teorema di Pitagora inoltre si ottiene: OB2 =
OC2 + BC2,
tradotto in funzioni trigonometriche:
. Per il teorema di Pitagora inoltre si ottiene: OB2 =
OC2 + BC2,
tradotto in funzioni trigonometriche: ![]() .
.
|
Angoli Funzioni |
|
|
|
|
|
|
|
|
|
Seno |
|
|
|
|
|
|
|
|
|
Coseno |
|
|
|
|
|
|
|
|
|
Tangente |
|
|
|
|
|
|
|
|
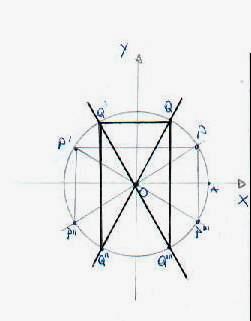
Gli archi associati sono quegli archi che hanno uguali in valore assoluto le funzioni goniometriche, per la proprietà degli angoli tra una retta che interseca due rette parallele. (vedi esempio).
Per il punto P sulla figura è:
|
P |
P' |
P'' |
P''' |
|
cos a |
cos (180° - a) = - cos a |
cos (180° + a) = - cos a |
cos ( 360° - a) = cos a |
|
sin a |
sin (180° - a) = sin a |
sin (180° + a) = - sin a |
sin ( 360° - a) = - sin a |
Per il punto Q sulla figura è:
|
Q |
Q' |
Q'' |
Q''' |
|
sin (90° - a) = cos a |
sin (90° + a) = cos a |
cos (270° - a) = - cos a |
cos (270° + a) = sin a |
|
cos (90° - a) = sin a |
cos (90° + a) = - sin a |
sin (270° - a) = - sin a |
sin (270° + a) = cos a |
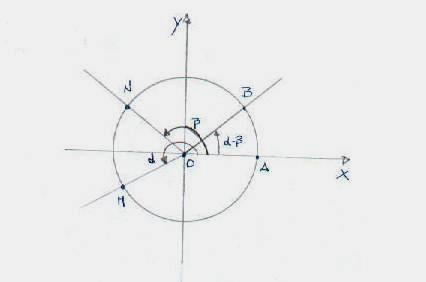
Ci sorge il problema sul come trovare il valore di seno e coseno di una
somma e differenza di un arco. Riportandoci alla figura soprastante. Allora introduciamo
le formule di somma e differenza di due archi noti. ![]() . Si vuole trovare la distanza AB e poi quella MN.
. Si vuole trovare la distanza AB e poi quella MN. ![]() ,
, ![]() . Ponendo le due misure uguali, ed elevando tutto al quadrato
in modo di eliminare le radici; in seguito svolgo i quadrati, mi rimane così la
FORMULA DI SOTTRAZIONE DEL COSENO:
. Ponendo le due misure uguali, ed elevando tutto al quadrato
in modo di eliminare le radici; in seguito svolgo i quadrati, mi rimane così la
FORMULA DI SOTTRAZIONE DEL COSENO: ![]() . Sostituendo b con -b si ha:
. Sostituendo b con -b si ha: ![]() , che è la FORMULA DI ADDIZIONE DEL COSENO. da queste ottengo
tutte le altre formule relative al seno e alla tangente.
, che è la FORMULA DI ADDIZIONE DEL COSENO. da queste ottengo
tutte le altre formule relative al seno e alla tangente. 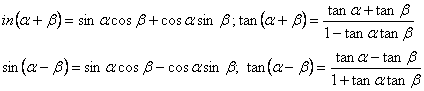
Esistono poi altre formule
fondamentali per le risoluzioni di problemi goniometrici.  .
.
 Funzione
Esponenziale e Logaritmica.
Funzione
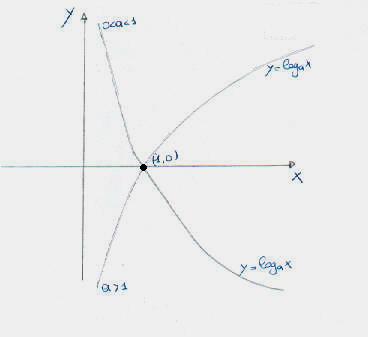
Esponenziale e Logaritmica.La funzione esponenziale è un
esempio di funzione trascendente, ed ha forma del tipo: ![]() . Per aver senso di parlare di equazione esponenziale bisogna
puntualizzare due cose: che a>0 e a 1. Per cui avrò che la base deve essere:
. Per aver senso di parlare di equazione esponenziale bisogna
puntualizzare due cose: che a>0 e a 1. Per cui avrò che la base deve essere: ![]() . Nel primo caso la curva sarà asintotica quando la x
diminuisce, mentre nel secondo caso sarà asintotica quando la x aumenta. Il
dominio della funzione sarà:
. Nel primo caso la curva sarà asintotica quando la x
diminuisce, mentre nel secondo caso sarà asintotica quando la x aumenta. Il
dominio della funzione sarà: ![]() e il condominio
e il condominio ![]() .
.
L'equazione ![]() ammette una sola
soluzione sempre che a e q siano positivi e a diverso 1. il numero x che
soddisfi l'equazione esponenziale si dice logaritmo del numero q, in base a e
scrive:
ammette una sola
soluzione sempre che a e q siano positivi e a diverso 1. il numero x che
soddisfi l'equazione esponenziale si dice logaritmo del numero q, in base a e
scrive: ![]() . Quindi possiamo dire che il logaritmo di un numero
(positivo), in una base (positiva, diversa da 1), è l'esponente che bisogna
dare alla base per ottenere il numero dato. Ci sono due casi particolari del
logaritmo:
. Quindi possiamo dire che il logaritmo di un numero
(positivo), in una base (positiva, diversa da 1), è l'esponente che bisogna
dare alla base per ottenere il numero dato. Ci sono due casi particolari del
logaritmo: ![]() .
.
Per risolvere una equazione, sia algebrica che trascendente, bisogna averla nella forma f(x)=0 oppure x=g(x); questo non è limitativo perché ci si può ricondurre ad una di queste forme. La risoluzione approssimata viene usata qualora ci troviamo di fronte ad equazioni algebriche e trascendenti non facili: cioè equazioni algebriche con grado superiore al 2° grado non riconducibili a un prodotto di polinomi di 1° e 2° grado, mentre quando dobbiamo risolvere equazioni trascendenti non riconducibili ad equazioni semplici (equazioni esponenziali: dove non si possono applicare i teoremi sulle potenze e sui logaritmi, oppure usare una variabile di appoggio; equazioni logaritmiche; equazioni goniometriche). La risoluzione approssimata si compone di due fasi distinte:
q Separazione delle radici, cioè il calcolo dell'intervallo in cui cade sicuramente una e una sola radice.
q Calcolo vero e proprio delle radici, applicando uno dei metodi studiati (tangenti, corde e punto medio).
Analizziamo più in specifico
le due fasi. Il problema della separazione delle radici reali si può risolvere
procedendo con il metodo grafico. Data l'equazione f(x)=0 si considera la funzione
come equazione soluzione del sistema formato da 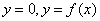 . Quindi si passa a fare il grafico orientativo della
funzione
. Quindi si passa a fare il grafico orientativo della
funzione ![]() e se il grafico è rappresentato bene si possono separare bene
le radici, e quindi trovare gli intervalli in cui cade una e una sola radice.
Si può procedere con un altro metodo, qualora la
e se il grafico è rappresentato bene si possono separare bene
le radici, e quindi trovare gli intervalli in cui cade una e una sola radice.
Si può procedere con un altro metodo, qualora la ![]() ha un grafico difficile da tracciare, che consiste nello
scomporre la
ha un grafico difficile da tracciare, che consiste nello
scomporre la ![]() in modo opportuno, in modo tale che sia facile da ricavare
l'intervallo in cui cade una e una sola radice.
in modo opportuno, in modo tale che sia facile da ricavare
l'intervallo in cui cade una e una sola radice.
Un'equazione differenziale è una
relazione che lega una variabile indipendente, una variabile dipendente e le
sue derivate d'ordine n. ![]() è un'equazione differenziale del primo grado perché il grado
massimo della derivata presente nell'equazione è uno. Le abbiamo introdotte e
quindi imparate a risolvere perché spesso in problemi fisici, elettronici;
possiamo incontrare equazioni in cui compaiono le variabili
è un'equazione differenziale del primo grado perché il grado
massimo della derivata presente nell'equazione è uno. Le abbiamo introdotte e
quindi imparate a risolvere perché spesso in problemi fisici, elettronici;
possiamo incontrare equazioni in cui compaiono le variabili ![]() e così via. Risolvere
un'equazione differenziale significa trovare la funzione
e così via. Risolvere
un'equazione differenziale significa trovare la funzione ![]() che, con le derivate (dipendenti dall'ordine dell'equazione
differenziale), per ogni x soddisfi l'equazione data. Fondamentale dal punto di
vista fisico è saper risolvere un problema di Cauchy. Un problema di Cauchy è
formato da un'equazione differenziale d'ordine n e da n condizioni iniziali;
risolverlo significa prima di tutto trovare l'integrale generale dell'equazione
differenziale e poi a quest'ultimo applicare le condizioni iniziali in modo
tale da avere una soluzione particolare dell'equazione differenziale di partenza.
che, con le derivate (dipendenti dall'ordine dell'equazione
differenziale), per ogni x soddisfi l'equazione data. Fondamentale dal punto di
vista fisico è saper risolvere un problema di Cauchy. Un problema di Cauchy è
formato da un'equazione differenziale d'ordine n e da n condizioni iniziali;
risolverlo significa prima di tutto trovare l'integrale generale dell'equazione
differenziale e poi a quest'ultimo applicare le condizioni iniziali in modo
tale da avere una soluzione particolare dell'equazione differenziale di partenza.
No,
non esiste. L'unica formula, che conosciamo, risolutiva d'equazioni è quella
per le equazioni di 2° grado. Per le equazioni differenziali dobbiamo fare una
casistica, secondo l'ordine e del tipo, in cui racchiuderemo i casi che
incontreremo più di frequente. Vediamo alcuni esempi di tipi d'equazioni
differenziali:
Si risolve in due parti:
A. Si determina la soluzione generale dell'equazione differenziale lineare omogenea corrispondente, che si risolve riportandola ad un'equazione differenziale a variabili separate o separabili.
B.
Si procede attraverso
l'applicazione del metodo di Lagrange. Cioè si pensa la costante c della
soluzione dell'equazione differenziale omogenea come variabile della x. Quindi
si applica il concetto di funzione soluzione e si sostituisce nell'equazione differenziale
di partenza. Avremo un'equazione in, integrando poi, e sostituendo la ![]() ottenuta nella
soluzione dell'equazione differenziale omogenea associata, avremo la soluzione
dell'equazione differenziale di partenza.
ottenuta nella
soluzione dell'equazione differenziale omogenea associata, avremo la soluzione
dell'equazione differenziale di partenza.
Come
sappiamo un integrale definito è valido solo quando l'intervallo è chiuso e
limitato; e la funzione deve essere continua nell'intervallo. Quando non
sussistono queste due condizioni o almeno una non possiamo risolvere un
integrale definito di una funzione ![]() . Bisogna allora introdurre il concetto d'integrale
improprio, che sono distinti dal tipo di condizione non verificata:1° Tipo:
intervallo non limitato;
. Bisogna allora introdurre il concetto d'integrale
improprio, che sono distinti dal tipo di condizione non verificata:1° Tipo:
intervallo non limitato;
2° Tipo: funzione non continua.
Vediamo il 1° Tipo. Si ha questo tipo
quando siamo nella situazione ![]() oppure
oppure ![]() . Bisogna quindi limitare l'intervallo d'integrazione, con
l'introduzione di nuovi intervalli
. Bisogna quindi limitare l'intervallo d'integrazione, con
l'introduzione di nuovi intervalli![]() oppure
oppure ![]() , e con l'aiuto dell'operatore limite. L'integrale
, e con l'aiuto dell'operatore limite. L'integrale ![]() diventerà
diventerà ![]() .
.
Per il secondo tipo di problemi si usa
anche qui l'operatore limite. Ad esempio:  ; sappiamo che il logaritmo a zero non ha senso di esser
posto. E quindi lavoriamo nell'intorno destro di zero. L'integrale di partenza
si ricondurrà al seguente calcolo:
; sappiamo che il logaritmo a zero non ha senso di esser
posto. E quindi lavoriamo nell'intorno destro di zero. L'integrale di partenza
si ricondurrà al seguente calcolo: 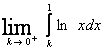 .
.
Un'equazione differenziale del 2°
ordine lineare non omogenea si risolve con un procedimento che ci porterà ad una
soluzione del tipo ![]() . O meglio
. O meglio ![]() , ove z è la soluzione dell'equazione differenziale omogenea
associata, e
, ove z è la soluzione dell'equazione differenziale omogenea
associata, e ![]() è la soluzione
particolare dell'equazione completa. La soluzione può essere trovata con il
metodo di Lagrange, che però risulta molto complesso a causa della presenza di
due costanti. Quindi la risoluzione anche qui prevede lo sviluppo di due fasi:
nel calcolo della z sono molto importanti due teoremi che ci dicono che se una
funzione
è la soluzione
particolare dell'equazione completa. La soluzione può essere trovata con il
metodo di Lagrange, che però risulta molto complesso a causa della presenza di
due costanti. Quindi la risoluzione anche qui prevede lo sviluppo di due fasi:
nel calcolo della z sono molto importanti due teoremi che ci dicono che se una
funzione ![]() è soluzione
dell'equazione differenziale allora anche
è soluzione
dell'equazione differenziale allora anche ![]() è soluzione; inoltre se
è soluzione; inoltre se ![]() e
e ![]() sono soluzioni
dell'equazioni differenziali allora anche
sono soluzioni
dell'equazioni differenziali allora anche ![]() sarà soluzione.
Attraverso la combinazione di questi due teoremi possiamo dire che con
sarà soluzione.
Attraverso la combinazione di questi due teoremi possiamo dire che con ![]() soluzioni
dell'equazione differenziale e linearmente indipendenti (il loro rapporto
diverso da una costante) la z sarà uguale a
soluzioni
dell'equazione differenziale e linearmente indipendenti (il loro rapporto
diverso da una costante) la z sarà uguale a ![]() . Diventa quindi molto importante la ricerca di
. Diventa quindi molto importante la ricerca di ![]() e per tale motivo ricerco tali funzioni nell'infinità
e per tale motivo ricerco tali funzioni nell'infinità ![]() . Applico il concetto di funzione soluzione, calcolo la
derivata prima e la derivata seconda, e mi accorgo che una funzione
. Applico il concetto di funzione soluzione, calcolo la
derivata prima e la derivata seconda, e mi accorgo che una funzione ![]() sarà soluzione solo
quando è soddisfatta l'equazione
sarà soluzione solo
quando è soddisfatta l'equazione 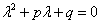 , in cui p e q sono gli stessi coefficienti dell'equazione
differenziale data. A seconda del tipo di
, in cui p e q sono gli stessi coefficienti dell'equazione
differenziale data. A seconda del tipo di ![]() (le soluzioni) avrò un
diverso tipo di
(le soluzioni) avrò un
diverso tipo di ![]() . E vediamo in particolare:
. E vediamo in particolare:
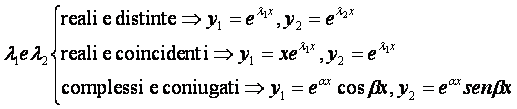 .
.
Per il calcolo di ![]() invece va fatto un attento esame della funzione al secondo
membro:
invece va fatto un attento esame della funzione al secondo
membro:
a)
![]() Polinomio di grado n
Polinomio di grado n
![]() allora
allora ![]()
![]() allora
allora ![]()
![]() allora
allora ![]()
b)
![]()
c)
![]()
d)
![]() , allora
, allora 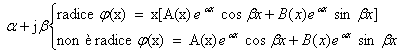
Una funzione in due variabili reali è una legge, f, di natura qualsiasi, che permetta di associare, ad ogni coppia di numeri reali, appartenenti ad un dominio D, sottoinsieme di, un numero reale z. di una funzione in due variabili non si può dare un grafico, ma si può fare solo uno studio. Per approfondire lo studio si devono seguire i seguenti passi:
Si individua il legame tra le variabili.
Si ricerca il dominio: spesso tale operazione può portare alla risoluzione di equazione, disequazioni oppure di sistemi. Si traccia il dominio su una coppia di assi cartesiani; associando alle equazioni, disequazioni il modello algebrico rappresentativo. Disegnando la funzione e scegliendo attraverso il punto indagine la porzione di piano in cui è valido o verificato il legame.
Calcolo il limite doppio o
superficiale: si utilizza il metodo di far tendere il punto P al punto ![]() lungo una qualsiasi
direzione del piano; si dimostra che il
lungo una qualsiasi
direzione del piano; si dimostra che il ![]() esiste se tale limite
non dipende dal modo in cui si tende a
esiste se tale limite
non dipende dal modo in cui si tende a ![]() ; altrimenti non esiste.
; altrimenti non esiste.
Si calcolano le derivate parziali;
Calcolo di eventuali punti di massimo e minimo: 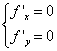 e si trovano
e si trovano ![]() .
.
Si calcola l'essiano: ![]() e si ottengono le
seguenti informazioni a secondo del valore dell'essiano:
e si ottengono le
seguenti informazioni a secondo del valore dell'essiano: ![]() ;
; ![]() ;
; ![]() ;
;![]() .
.
Sia ![]() una funzione continua nell'intervallo chiuso
una funzione continua nell'intervallo chiuso ![]() e derivabile in
e derivabile in ![]() ; se essa assume agli estremi a e b dell'intervallo valori
uguali allora esiste almeno un punto c all'interno all'intervallo nel quale la
derivata della funzione è nulla.
; se essa assume agli estremi a e b dell'intervallo valori
uguali allora esiste almeno un punto c all'interno all'intervallo nel quale la
derivata della funzione è nulla.
Siano date due funzioni ![]() e
e ![]() entrambe continue nell'intervallo chiuso
entrambe continue nell'intervallo chiuso ![]() e derivabile in
e derivabile in ![]() ; inoltre la funzione
; inoltre la funzione ![]() ammette derivata diversa da zero in tutti i punti
dell'intervallo
ammette derivata diversa da zero in tutti i punti
dell'intervallo ![]() ; esiste almeno un punto c, interno all'intervallo, nel quale
si verifica che
; esiste almeno un punto c, interno all'intervallo, nel quale
si verifica che ![]() .
.
Sia data una funzione ![]() continua nell'intervallo
continua nell'intervallo ![]() e derivabile in
e derivabile in ![]() ; esiste allora almeno un punto c, interno all'intervallo,
nel quale si verifica che :
; esiste allora almeno un punto c, interno all'intervallo,
nel quale si verifica che :
![]() .
.
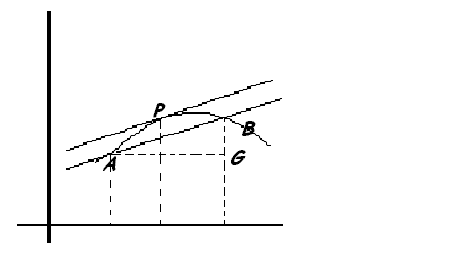
Il teorema di Lagrange dal punto di
vista geometrico si può interpretare così: "Si consideri il grafico della
funzione ![]() , sia l'arco AB quello compreso tra a e b. Si conduca la
corda AB; possiamo pensare che sull'arco AB esiste almeno un punto P nel quale
la tangente sia parallela alla corda AB.
, sia l'arco AB quello compreso tra a e b. Si conduca la
corda AB; possiamo pensare che sull'arco AB esiste almeno un punto P nel quale
la tangente sia parallela alla corda AB.
Il limite del rapporto di due
funzioni, che si presenta sotto la forma inderminata ![]() , è uguale al limite del rapporto delle loro derivate. Si può
dimostrare che la regola di De L'Hopital si può applicare anche per la forma
indeterminata
, è uguale al limite del rapporto delle loro derivate. Si può
dimostrare che la regola di De L'Hopital si può applicare anche per la forma
indeterminata ![]() . Quindi si trova:
. Quindi si trova: ![]() .
.
Avendo una funzione y=f(x), per studiare la funzione devo seguire il seguente algoritmo:
Riconoscere il tipo di funzione;
v Trovare il dominio d'esistenza della funzione;
Trovare le eventuali intersezioni con gli assi;
v Cercare la variabilità della funzione;Riportare i dati ottenuti sugli assi cartesiani per tracciare un grafico orientativo della funzione.
Se la funzione ![]() è continua nell'intervallo chiuso
è continua nell'intervallo chiuso ![]() , e se risulta
, e se risulta ![]() allora l'equazione
allora l'equazione ![]() ha almeno una radice all'interno di tale intervallo.
ha almeno una radice all'interno di tale intervallo.
1° Teorema: Sia ![]() una funzione derivabile e continua nell'intervallo chiuso
una funzione derivabile e continua nell'intervallo chiuso ![]() . Sia
. Sia ![]() e la
e la ![]() diversa da zero nell'intervallo
diversa da zero nell'intervallo
![]() allora esiste una soluzione all'interno dell'intervallo.
allora esiste una soluzione all'interno dell'intervallo.
2° Teorema: Sia ![]() una funzione derivabile e continua nell'intervallo chiuso
una funzione derivabile e continua nell'intervallo chiuso ![]() e derivabile almeno
due volte. Sia
e derivabile almeno
due volte. Sia ![]() e la
e la ![]() sempre positiva o
sempre negativa allora esiste una soluzione all'interno dell'intervallo.
sempre positiva o
sempre negativa allora esiste una soluzione all'interno dell'intervallo.
Data una successione di numeri ![]() è possibile dare un significato alla scrittura
è possibile dare un significato alla scrittura ![]() che si può chiamare
serie numerica. Come è ben noto la somma d'infiniti termini rappresenta
un'espressione priva di significato e quindi è necessaria un'apposita
definizione. Per questo si utilizza l'algoritmo limite: si incomincia a sommare
i termini uno ad uno
che si può chiamare
serie numerica. Come è ben noto la somma d'infiniti termini rappresenta
un'espressione priva di significato e quindi è necessaria un'apposita
definizione. Per questo si utilizza l'algoritmo limite: si incomincia a sommare
i termini uno ad uno ![]() ,
, ![]() ,
,![]() , .,
, ., ![]() . Queste si chiameranno le ridotte della serie o somme
parziali e formeranno una successione
. Queste si chiameranno le ridotte della serie o somme
parziali e formeranno una successione ![]() detta appunto
successione delle somme parziali associata alla serie. Il termine
detta appunto
successione delle somme parziali associata alla serie. Il termine ![]() è detto somma parziale
n-esima di indice n. Passando al limite
è detto somma parziale
n-esima di indice n. Passando al limite ![]() . Questo limite avrà tre casi distinti:
. Questo limite avrà tre casi distinti:
Se esiste il limite ed è finito; ![]() e affermeremo che la serie è convergente ed ha per somma s;
e affermeremo che la serie è convergente ed ha per somma s;
Se il limite è infinito affermeremo che la serie è divergente;
Se il limite non esiste sosterremo che la serie è indeterminata.
L'importante per una serie è stabilirne il carattere, e per fare ciò si confronta con le serie principali, di cui conosciamo sia le caratteristiche sia il carattere, oppure con i criteri di confronto. I criteri del confronto sono diversi a secondo del tipo di serie che ci troviamo di fronte: le serie si dividono in quelle a termini di segno costante (a sua volta in quelle di segno positivo e in quelle di segno negativo) e in quelle di segno alterno(anche qui ci sono quelle di segno alterno e quelle di segno qualunque). Vediamo alcune serie fondamentali.
La serie ha come termine generale ![]() . Si ha
. Si ha ![]() , il termine generale può anche essere scritto come
, il termine generale può anche essere scritto come ![]() , quindi la somma diventa
, quindi la somma diventa![]() . Riducendo si ottiene
. Riducendo si ottiene ![]() , calcolando il limite
, calcolando il limite ![]() . Potremo concludere che la serie di Mengoli è convergente ed
ha per somma il valore 1.
. Potremo concludere che la serie di Mengoli è convergente ed
ha per somma il valore 1.
![]() . La caratteristica della serie geometrica sta nel fatto che
tra un termine e il suo precedente il loro rapporto vale sempre q. A secondo
del valore di q la serie avrà diversi comportamenti. Con
. La caratteristica della serie geometrica sta nel fatto che
tra un termine e il suo precedente il loro rapporto vale sempre q. A secondo
del valore di q la serie avrà diversi comportamenti. Con ![]() la serie converge ed ha per somma il valore uno.
la serie converge ed ha per somma il valore uno. ![]() allora si ottiene
allora si ottiene ![]() . Mentre con
. Mentre con ![]() la serie diverge, e con
la serie diverge, e con ![]() la serie diventa indeterminata. Nel caso in cui
la serie diventa indeterminata. Nel caso in cui ![]() e ci sono termini che non fanno parte della serie geometrica,
ad esempio
e ci sono termini che non fanno parte della serie geometrica,
ad esempio ![]() , la somma per
, la somma per ![]() diventa
diventa ![]() .
.
![]() . La serie armonica è formata dai reciproci dei numeri naturali.
La serie armonica è sempre divergente, anche se la condizione necessaria per la
convergenza di una serie è rispettata:
. La serie armonica è formata dai reciproci dei numeri naturali.
La serie armonica è sempre divergente, anche se la condizione necessaria per la
convergenza di una serie è rispettata: ![]() è un infinitesimo per
è un infinitesimo per ![]() .
.
![]() Tale serie risulta
divergente per
Tale serie risulta
divergente per ![]() e convergente per
e convergente per ![]() . Questo ci è stato permesso grazie al criterio integrale che
ci ha permesso di individuare la discussione sulla convergenza. Sapendo che
. Questo ci è stato permesso grazie al criterio integrale che
ci ha permesso di individuare la discussione sulla convergenza. Sapendo che ![]() la serie è la serie
armonica, che sappiamo essere sempre divergente, consideriamo
la serie è la serie
armonica, che sappiamo essere sempre divergente, consideriamo ![]() , per
, per ![]() e
e ![]() ,continua e decrescente, tale che
,continua e decrescente, tale che ![]() . Possiamo applicare il criterio integrale:
. Possiamo applicare il criterio integrale: ![]() . Se
. Se ![]() allora
allora ![]() se invece
se invece ![]() allora
allora ![]() . Quindi giungiamo alla conclusione che per
. Quindi giungiamo alla conclusione che per ![]() la funzione
la funzione ![]() è finita e la serie
converge;
è finita e la serie
converge; ![]() la funzione
la funzione![]() è infinita e la serie diverge.
è infinita e la serie diverge.
Osserviamo ora i criteri di confronto delle serie a termini positivi.
Date due serie di termini positivi ![]() , sia per
, sia per ![]() e
e ![]() .
.
Se la serie maggiorante ![]() è convergente allora anche la serie
è convergente allora anche la serie ![]() è convergente.
è convergente.
Se la serie minorante ![]() è divergente, allora
anche l'altra serie è divergente.
è divergente, allora
anche l'altra serie è divergente.
Date due serie di termini positivi ![]() , si supponga che esista il limite
, si supponga che esista il limite ![]() .
.
Se la serie ![]() è convergente ed il limite
è convergente ed il limite ![]() è finito (
è finito (![]() ) allora anche la serie
) allora anche la serie ![]() è convergente.
è convergente.
Se la serie ![]() è divergente e il limite l è non nullo allora anche l'altra
serie è divergente.
è divergente e il limite l è non nullo allora anche l'altra
serie è divergente.
Data la serie a termini positivi ![]() e se esiste finito il
limite
e se esiste finito il
limite ![]() allora:
allora:
La serie converge per ![]() ;
;
La serie diverge per ![]() ;
;
Se il limite vale ![]() il criterio di D'Alambert non fornisce alcun'indicazione sul
carattere della serie.
il criterio di D'Alambert non fornisce alcun'indicazione sul
carattere della serie.
Data la serie a termini positivi ![]() se esiste finito il
limite
se esiste finito il
limite ![]() allora si ha:
allora si ha:
la serie converge per ![]() ;
;
la serie diverge per ![]() ;
;
se il limite vale ![]() il criterio di Cauchy non fornisce alcuna indicazione sul
carattere della serie.
il criterio di Cauchy non fornisce alcuna indicazione sul
carattere della serie.
I teoremi descritti sopra possono essere applicati alle serie a termini di segno negativo. Per stabilire il carattere di una serie di segno alterno si usa il criterio di Leibniz che dice:
"Se i termini di una serie di segno
alterno sono decrescenti in valore assoluto (![]() ), e il termine generale è un infinitesimo per
), e il termine generale è un infinitesimo per ![]() , allora la serie convergente ed ha per somma s, che è
positiva ed è minore del primo termine
, allora la serie convergente ed ha per somma s, che è
positiva ed è minore del primo termine ![]() ."
."
Per una serie a termini di segno qualunque si usa stabilire il carattere con il seguente teorema:
"Data una serie di segno qualunque ![]() si dice assolutamente
convergente quando la serie formata dai valori assoluti dei suoi termini è
convergente."
si dice assolutamente
convergente quando la serie formata dai valori assoluti dei suoi termini è
convergente."
Per le serie di funzioni possono
essere ripetute le considerazioni dette in precedenza per le serie numeriche,
quindi: ![]() , diremo che la serie è convergente nel punto
, diremo che la serie è convergente nel punto ![]() , se risulta la serie numerica formata dai valori delle
funzioni della serie, per
, se risulta la serie numerica formata dai valori delle
funzioni della serie, per ![]() , è convergente. Lo studio di una serie di funzioni comporta
lo svolgimento di un preciso algoritmo:
, è convergente. Lo studio di una serie di funzioni comporta
lo svolgimento di un preciso algoritmo:
stabilire se la serie converge o meno;
individuare il dominio di convergenza;
stabilire se si tratta di semplice o uniforme convergenza;
determinare se possibile la somma della serie.
Il punto 1 si risolve utilizzando i criteri usati per stabilire il carattere di una serie numerica: 1° e 2° criterio del confronto, D'Alambert, Cauchy. Nel punto 2 si procede calcolando il dominio di convergenza ovvero l'insieme di tutti quei valori in cui la serie è convergente. Per stabilire se una serie di funzioni converge semplicemente oppure converge uniformemente bisognerà ricorrere a particolari criteri. È importante che una serie di funzioni sia uniformemente convergente perché solo in questo caso è possibile applicare i teoremi del limite, di continuità, di integrazione, di derivazione. Bisognerà quindi distinguere cosa si intende per convergenza puntuale e convergenza uniforme.
Considerando la serie di funzioni ![]() e sia definita in D.
Al variare della x si avrà una serie numerica convergente, ciascuna della quale
avrà per somma una diversa funzione
e sia definita in D.
Al variare della x si avrà una serie numerica convergente, ciascuna della quale
avrà per somma una diversa funzione ![]() . Diremo che la serie converge in D ed ha per somma
. Diremo che la serie converge in D ed ha per somma ![]() quando fissato un
generico
quando fissato un
generico ![]() ed un arbitrario
numero reale
ed un arbitrario
numero reale ![]() , è possibile determinare un indice
, è possibile determinare un indice ![]() , dipendente da
, dipendente da ![]() e da x tale che per
ogni
e da x tale che per
ogni ![]() si abbia:
si abbia: ![]() .
.
La convergenza uniforme si ha quando:
è possibile determinare un indice ![]() , che dipende solo da
, che dipende solo da ![]() , tale che per ogni
, tale che per ogni ![]() si abbia:
si abbia: ![]() . Per stabilire se si tratta di convergenza uniforme ci
aiutano due teoremi:
. Per stabilire se si tratta di convergenza uniforme ci
aiutano due teoremi:
Sia data una serie di funzioni ![]() ed una serie numerica,
a termini positivi, convergente,
ed una serie numerica,
a termini positivi, convergente, ![]()
![]() . Se per tutti gli x di un certo insieme
. Se per tutti gli x di un certo insieme ![]() risulta
risulta ![]() allora la serie è
uniformemente convergente.
allora la serie è
uniformemente convergente.
Sia data una serie di funzioni ![]() , il cui termine generale possa essere scritto nella forma
, il cui termine generale possa essere scritto nella forma ![]() ; se
; se ![]() è una funzione limitata in un insieme E, e se la serie
è una funzione limitata in un insieme E, e se la serie ![]() è uniformemente
convergente in E, allora anche la serie data è uniformemente convergente.
è uniformemente
convergente in E, allora anche la serie data è uniformemente convergente.
Sia ![]() una serie di funzioni
uniformemente convergente, in un intervallo E, verso la funzione
una serie di funzioni
uniformemente convergente, in un intervallo E, verso la funzione ![]() . Se, per ogni n, le funzioni
. Se, per ogni n, le funzioni ![]() sono continue in E, allora anche la funzione somma
sono continue in E, allora anche la funzione somma ![]() è continua in E.
è continua in E.
Sia data ![]() una serie di funzioni
continue, uniformemente convergente nell'intervallo
una serie di funzioni
continue, uniformemente convergente nell'intervallo ![]() verso la funzione
verso la funzione ![]() . Allora si ha
. Allora si ha 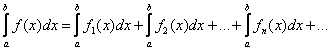 ovvero
ovvero 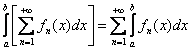 .
.
Sia data la serie di funzioni ![]() convergente in
convergente in ![]() verso la funzione
verso la funzione ![]() :
: ![]() . Le funzioni
. Le funzioni ![]() siano, per ogni n,
derivabile e dotate di derivata continua nell'intervallo di convergenza; la
serie derivata
siano, per ogni n,
derivabile e dotate di derivata continua nell'intervallo di convergenza; la
serie derivata ![]() sia uniformemente
convergente in
sia uniformemente
convergente in ![]() , allora la funzione
, allora la funzione ![]() risulta derivabile.
risulta derivabile.
La trasformata di Laplace è un
operatore funzionale, molto importante per la risoluzione di particolari
problemi scientifici e tecnici. Le trasformate vengono utilizzate per la
risoluzione particolare di alcuni integrali impropri. La trasformata è definita
come: 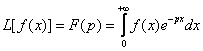 . Per applicare ad una f(x) la trasformata di Laplace bisogna
che vengano rispettate le seguenti condizioni:
. Per applicare ad una f(x) la trasformata di Laplace bisogna
che vengano rispettate le seguenti condizioni:
![]() continua nell'intervallo e integrabile nell'integrale
continua nell'intervallo e integrabile nell'integrale ![]() con
con ![]() ;
;
La x sia una variabile di tipo reale;
La p sia, anch'essa una variabile di tipo reale.
La variabile p può essere interpretata, per il fisico e per l'elettronico, come una variabile complessa nello studio di sistemi con ingresso periodico.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025