286 a.C.  1552 1564 1598 1608 1630

Archimede (287 a.C.-212 a.C.): calcolo di aree delimitate dalla curva y=f(x), dall'asse x e dalle rette x=0 e x=a, per curve particolari;

Valerio (1552-1618): generalizzazione del calcolo di aree per curve continue e monotone;

principio generale: se A_nA e B_nB, e se =K (cost.) al variare di n, allora =K;

paradossi dalla determinazione di aree (cfr appunti del prof. Piscione) calcolate tramite il metodo degli indivisibili.

1. Il contesto dell'opera di Cavalieri

Bonaventura Cavalieri visse tra il 1598 ed il 1647.

Lo scenario nel quale si collocò la sua vita e la sua opera fu pieno di evoluzioni dal punto di vista matematico.

Luca Valerio (1552-1618) si era occupato nel periodo precedente della

determinazione di aree e volumi tramite processi di approssimazione dall'esterno e dall'interno; si affacciavano in quegli anni i problemi relativi ai paradossi dell'infinito, e nasceva l'analisi infinitesimale.

Cavalieri ebbe il pregio di incontrare Galileo, del quale subì forte influenza.

La fama di Cavalieri è legata alla "Geometria indivisibilus continuorum nova quadam ratione promota" (1635). In questo trattato Cavalieri usò il "metodo degli indivisibili" per determinare aree e volumi.

1.1 Gli indivisibili

Cavalieri, dall'analisi e dalle riflessioni indotte dai processi di approssimazione di aree e volumi ottenute tramite la somma di un numero "grande" di contributi, trasse l'acquisizione che i contributi di un'area siano assimilabili a segmenti paralleli equidistanti, e che i contributi di un volume siano assimilabili ad aree piane parallele.

Questo numero indefinito di "elementi" che costituivano (risp.) aree e volumi erano detti "indivisibili" (risp.) di area e volume.

In realtà, il metodo degli indivisibili era già stato impiegato da Archimede e nel Rinascimento se ne occuparono, oltre allo stesso Cavalieri, anche Leonardo da Vinci, Luca Valerio, Galilei, Torricelli.

Cavalieri, e così i sostenitori degli "indivisibili" (detti "indivisibilisti"), sosteneva che una retta è composta da punti come un rosario da grani, che un piano è composto da rette come una stoffa da fili e che un volume è composto da aree piane come un libro da pagine.

Cavalieri, pur ammettendo la moltitudine (indefinitezza) degli indivisibili, sosteneva che essi fossero in numero finito, mentre molti indivisibilisti si spinsero a supporre che fossero una moltitudine infinita.

La teoria di Cavalieri, e le sue dimostrazioni sulla determinazione di volumi, si basò sul principio seguente:

"se due solidi hanno altezze uguali e se le sezioni fatte con i piani paralleli alle basi e posti a distanze uguali da esse hanno sempre un rapporto dato, allora anche i volumi dei due solidi hanno lo stesso rapporto"

ovvero il rapporto costante tra gli indivisibili di volume (aree) determina il rapporto costante tra i volumi.

In modo analogo dicasi per le aree e per gli indivisibili di area (segmenti).

Area dell'ellisse

A livello esemplificativo si può illustrare come Cavalieri determinò l'area dell'ellisse, impiegando il principio degli indivisibili.

Date un'ellisse ed una circonferenza come in figura:

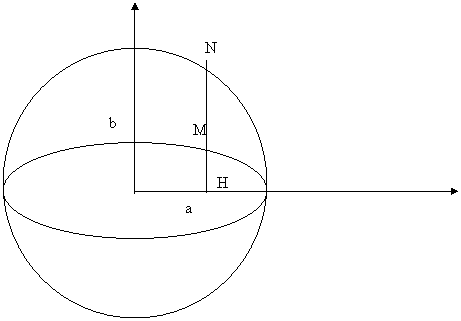
H

di equazioni: C: x²+y²=a²

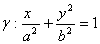
Cavalieri osservò che la semicorda NH del cerchio ed il segmento MH, al variare di x= OH, mantengono un rapporto costante pari ad .

Tramite il "principio di Cavalieri", egli dedusse che l'area del semicerchio, i cui indivisibili sono le semicorde, e l'area della semiellisse, i cui indivisibili sono i segmenti MH, debbono avere perciò rapporto costante pari ad .

Posto infatti OH=x, dall'applicazione del teorema di Pitagora al triangolo OHN, si ottiene che:

NH=

Inoltre, dalla condizione di appartenenza del punto M all'ellisse, deriva che:

HM=

Perciò il rapporto risulta pari a:

/ ()

ovvero, semplificando, si ottiene che risulta pari ad .

Ebbene, essendo il semicerchio e la semiellisse formate da indivisibili che hanno rapporto costante, anche le loro superfici hanno rapporto costante pari ad , ed essendo:

area(cerchio)=

e:

area(cerchio)/area(ellisse) =a/b

si ottiene infine:

area(ellisse)=/(a/b)=

L'infinito e gli indivisibili

Mentre Cavalieri sosteneva la finitezza degli indivisibili, la corrente degli indivisibilisti si spinse ammettendone l'infinitezza. Per esempio Galileo sosteneva che tutti gli oggetti fossero formati da un "continuo" di parti piccole ma misurabili e che "ogni parte dell'infinito è infinita" anche se "si sa bene che una linea di cento palmi è maggiore di una di un palmo solo, non però i punti di quella sono più dei punti di questa, ma e questi e quelli sono infiniti".

Gli anni di Galilei furono caratterizzati da un'attenzione al concetto di "infinito"ed al rapporto, spesso di collisione, dell'applicazione di teorie dell'infinito a contesti di finitezza.

Per esempio si consideri un triangolo ABC, di base AB, si tracci il segmento di estremi sui lati obliqui, distante dalla base metà dell'altezza, così come in figura:

C

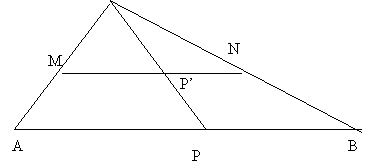
Dalle proprietà di similitudine dei triangoli (tre angoli congruenti) si ha che MN ha lunghezza metà di AB. Eppure, se si considera una semiretta uscente dal vertice che interseca MN e AB rispettivamente in P' ed in P, si può notare che la funzione f che associa P' a P (o viceversa), è biunivoca, per cui si deve dedurre che AB e MN posseggono lo stesso numero di punti.

Questo appare come un paradosso se noi intendiamo attribuire le proprietà del finito ad oggetti di natura infinita.

Come disse Galileo "stimo che questi attributi di maggioranza, minorità ed equalità non convenghino a gl'infiniti, dei quali non si può dire, uno esser maggiore o minore o eguale all'altro".

Anche Torricelli (1608-1647) ebbe contatto con la teoria degli indivisibili dei quali seppe rivelare l'importanza, e con le proprietà dell'infinito, riscontrando ancora l'inapplicabilità delle proprietà del finito agli oggetti di natura infinita.

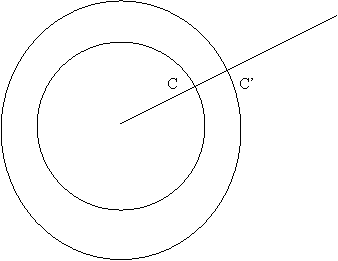
Infatti, per esempio, egli osservò che due circonferenze concentriche hanno lo stesso numero di punti, eppure hanno lunghezza differente!

Evangelista Torricelli

Evangelista Torricelli (Faenza 1608-Firenze 1647) matematico e fisico italiano, studiò a Faenza presso il collegio dei gesuiti e quindi a Roma, dove seguì i corsi di Benedetto Castelli, allievo di Galileo.

Nell'ottobre 1641, su interessamento di Castelli venne ad Arcetri per assistere come segretario il vecchio e cieco Galileo, il quale però poco dopo si spegneva (8 gennaio 1642). Torricelli rimase quindi a Firenze, dove fu nominato matematico e filosofo del granduca; per lui venne rinnovata la lettura di matematiche nello studio fiorentino.

L'unico lavoro che pubblicò mentre era in vita è l'Opera geometrica (1644), in cui inserì il precedente De motu; altri suoi scritti rimasero a lungo inediti.

Torricelli occupa un posto di grande rilievo nella storia dello sviluppo del calcolo infinitesimale per le sue fondamentali ricerche geometriche, nello svolgimento delle quali applicò il metodo degli indivisibili di Cavalieri.

Torricelli inoltre ampliò questa nozione, includendo negli indivisibili anche gli indivisibili curvilinei. Gli indivisibili curvi "nelle figure piane sono le periferie dei circoli, e nelle figure solide, sono superfici sferiche, cilindriche e coniche".

Il principio fondamentale degli indivisibili curvi si può enunciare così:

Per confrontare due figure, intersechiamo la prima, racchiusa da un sistema di curve, e la seconda, racchiusa da un sistema di rette parallele: se ogni indivisibile curvo della prima figura è corrispondente ad un indivisibile rettilineo della seconda, (quindi se ogni trapezoide infinitesimo della prima figura è equivalente al quadrangolo infinitesimo della seconda figura), allora le due figure hanno la stessa area.

Il principio degli indivisibili curvi venne applicato anche nel calcolo del volume del solido iperbolico "acutissimo".

Mediante essi Torricelli dimostrò che "il solido acuto iperbolico infinitamente lungo detto tromba di Gabriele, tagliato con un piano perpendicolare all'asse, insieme con il cilindro della sua base, è uguale ad un cilindro retto, la cui base sia l'asse della iperbola, e la cui altezza sia equale al semidiametro della base del solido acuto".

Dimostrò quindi che tale solido, pur avendo una superficie infinita, possiede un volume finito. Questo apparve come un paradosso per molto tempo ma significò, in termini moderni, l'aver prodotto il primo esempio di calcolo di un integrale improprio.

Torricelli lasciò innumerevoli manoscritti, tra questi risultano gli studi sulle tangenti e la quadratura delle infinite parabole e delle infinite spirali, oltre che la regola per la determinazione del baricentro di una figura qualunque (purché dotata di asse).
 

La morte contemporanea di Torricelli e di Cavalieri segna la fine della grande stagione della geometria italiana apertasi con il Rinascimento e largamente influenzata dalla figura di Galileo.

Torricelli fu pioniere nel settore delle serie infinite. Nella sua opera intitolata De dimensione parabolae del 1644, egli considerò una successione decrescente di termini positivi a₀, a₁, a₂ .. e ha mostrato che la corrispondente serie telescopica:

(a₀- a₁)+( a₁- a₂)+...converge necessariamente ad a₀-L, dove L è il limite della successione.

Area del cerchio

Per il calcolo dell'area del cerchio, Torricelli ne considera gli indivisibili, individuandoli nelle circonferenze concentriche al cerchio dato.

Così come in figura, Torricelli confronta l'area del cerchio di centro in A e raggio AB=r con l'area del triangolo ABC, di base lunga 2r, confrontando gli indivisibili del cerchio (circonferenze concentriche di raggio AE=x) con gli indivisibili del triangolo (segmenti EF) (cfr appunti Biscione).

Dalla similitudine dei triangoli AEF e ABC si ha la proporzionalità dei lati del triangolo e quindi si ottiene che EF= (2r*x)/r = 2x (lunghezza dell'indivisibile del triangolo ABC).

Ma essendo c'=2x (lunghezza dell'indivisibile curvo del cerchio), si ha che EF= c'.

Per il teorema degli indivisibili curvi abbiamo che l'area del cerchio è pari all'area del triangolo, ovvero area(cerchio)=area(triangolo)= (2r*r)/2=r².