LIMITI DI FUNZIONI - IL CONCETTO DI LIMITE

x→c

quando, in corrispondenza ad un n° positivo ε arbitrario, è sempre possibile determinare un intorno completo H del punto c tale che, per ogni x di H, escluso c, risulti soddisfatta la disequazione:

|f(x) - | < ε

LIMITE INFINITO DI UNA FUNZ. IN 1 PUNTO:

Si dice che la funzione f (x), per x che tende a c, ha per limite l'infinito, e si scrive: 242b19c

lim   f (x) = ∞

x→c

quando, in corrispondenza ad un n° positivo M arbitrario, è sempre possibile determinare un intorno completo H del punto c tale che, per ogni x di H, distinto da c, risulti soddisfatta la disequazione:

|f(x)| > M

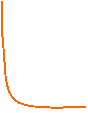
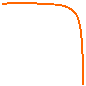
LIMITE DX E LIMITE SX DI UNA FUNZ. IN 1 PUNTO c:

Si dice che il n° ℓ è il limite dx della funzione f (x), per x che tende a c, e si scrive: 242b19c

lim   f (x) = ℓ

x→c

quando il valore ℓ è riassunto dalla funzione solo in un intorno dx.

y

x

Si definisce limite sx della funzione f (x), per x che tende a c, e si scrive: 242b19c

lim   f (x) = ℓ

x→c

quando la funzione assume il valore del limite solo in un intorno sx. Può capitare che il limite dx e quello sx siano diversi fra loro in tal caso la funzione si dice discontinua nel punto c.

LIMITI E CONTINUITA'

f (x) è continua in un punto x₀ appartenente al suo D se:

lim f (x) = lim f (x) = f (x₀)

x→x₀^- x x₀⁺

Ogni funzione ottenuta mediante somme, prodotti, quozienti e composizione a partire dalle funzioni elementari e dalla funzione valore assoluto è continua in ogni punto del suo D.

FORME DI INDETERMINAZIONE

Forme di Indeterminazioni: sono dei limiti in cui il risultato è il seguente:

∞ 0

+ ∞; - ∞ 0 . ± ∞

∞ 0

Quando ho la F. di I. ^∞/_∞ si raccoglie sia a Numeratore che a Denominatore la x di grado massimo.

Regole:

Se il grado del Numeratore è > del Denominatore il risultato sarà sempre ∞.

Se il grado del Numeratore è < del Denominatore il risultato sarà sempre 0.

Se il grado del Numeratore e del Denominatore è lo stesso il risultato del limite sarà sempre un numero.

Esempio 1

3 - 4x³ ∞ x³ (3/x³ - 4) - 4x² + ∞²

lim = = = = = ∞

x→ 1 - x ∞ x (1/x - 1) - 1 - 1

Esempio 2

1 ∞ 1 1 1

lim = = = = = 0

x→ x + 1 ∞ x (1 + 1/x) x ∞

Esempio 3

x ∞ x

lim = = = 1

x→ x + 1 ∞ x (1 + 1/x)

Ricordare che:

0 n° n° 0 ∞

= 0 = ± ∞ = 0 = 0 = ± ∞

n° 0 ∞ ∞ n°

FORME INDETERMINATE DEL TIPO: +

lim   e^x . \³ (2 + x)² = e^∞ . \³ (2 + ∞)² = ∞ . ∞ = + ∞

x→

FORME INDETERMINATE DEL TIPO: 0

1

lim ln (x) . = 0 . ±

x→ x - 1

0

FORME INDETERMINATE DEL TIPO:

0

x² + 5x - 6 1 + 5 - 6 0

lim = =

x→ x² + x - 2 1 + 1 - 2 0

FORME INDETERMINATE DEL TIPO:

∞

x⁴ + 5x² - 7 ∞ x⁴ (1 + 5/x² - 7/x⁴) x² - ∞

lim = = = = + ∞

x→+ ∞ 2x² + 3x - 1 ∞ x² (2 + 3/x - 1/x²) 2 2

LIMITI NOTEVOLI

Limiti Notevoli: sono i limiti in cui la x tende a 0 delle funzioni trigonometriche:

sin (x)

lim = 1

x→0 x

1 - cos (x) 1

lim =

x→0 x² 2

e^x - 1

lim = 1

x→0 x

log (1 + x)

lim = 1

x→0 x

Ricordiamo che la tg è data dal rapporto fra sin e cos