|
|
| |
LA RETTA:
Distanza tra due punti con coordinate note: d=![]() FUNZIONE
PARI: f(-x)=f(x)
FUNZIONE
PARI: f(-x)=f(x)
Distanza tra due punti aventi la stessa
ordinata: d=![]() FUNZIONE
DISPARI: f(-x)=-f(x) 727d34h
FUNZIONE
DISPARI: f(-x)=-f(x) 727d34h
Distanza tra due punti aventi la stessa
ascissa: d=![]()
Distanza tra due punti appartenenti alla
stessa retta con m noto: d=![]()
Distanza di P(x1; y1)
dalla retta ax+bx+c=0: d=![]()
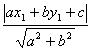
Distanza di P(x1; y1)
dalla retta y=mx+q: d=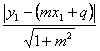
Coordinate baricentro di un triangolo: xG=![]() ; xG=
; xG=![]()
Coordinate punto medio di un segmento con gli
estremi noti: xm=![]() ; ym=
; ym=![]()
Coordinate simmetrico di A(x; y) rispetto a
P(a; b): 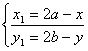
Formula di interpolazione lineare di P(x0;
y0) tra A(x1; y1) e B(x2; y2):
![]()
Traslazione degli assi (O1=a; b):
nuove coordinate di P(x; y): 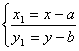
nuove coordinate di una retta: 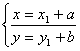
Equazione generale della retta in forma implicita: ax+bx+c=0
Equazione generale della retta in forma esplicita: y=mx+q
Equazione fascio improprio di rette: y=mx+q con m noto
Equazione retta parallela all'asse x: y=costante
Equazione retta parallelay all'asse y: x=costante
Equazione asse y: x=0
Equazione retta passante per due punti: ![]()
Equazione fascio rette di centro P(x1;
y1): ![]()
Coefficiente angolare (se č positivo la
funzione č crescente) retta passante per due punti: m=![]()
Condizione di parallelismo: m=m1
Condizione di perpendicolaritā: m=![]()
Equazione asse di un segmento di estremi A(x1;
y1) e B(x2; y2): ![]()
Equazione bisettrici degli angoli formati
dalle rette r=![]() e s=
e s=![]() :
: 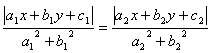
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025