Integrali definiti e impropri

Quindi anche in questa parte dobbiamo ideare un programma in linguaggio C++ che, con appositi input possa rispondere alla nostra domanda.

Teoria

Per capire come abbiamo ideato il programma in C++ è importante dare alcune nozioni teoriche sugli integrali:

prima parte

la domanda principale che cercheremo di rispondere con queste note teoriche è "Come si può calcolare un integrale definito in un intervallo da" a" a "b"? ".

Innanzitutto è importante definire una funzione f(x) continua e limitata nell'intervallo [a,b] , partendo dalla definizione geometrica dell'integrale cioè l'aera di un trapezoide costruito sotto la curva della funzione studiata:

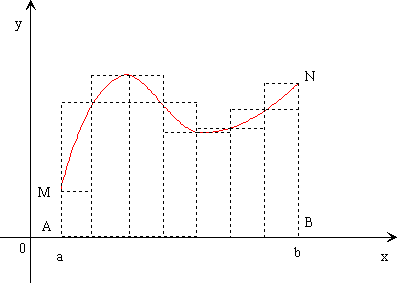
Per dare però una definizione rigorosa dell'area di un trapezoide che come si può notare è delimitata dalla linea curva che rappresenta l'andamento della funzione, bisogna fare un piccolo artificio. A tale scopo dividiamo l'intervallo [a,b] in un certo numero n di parti uguali e, detta ∆x = (b-a)/n l'ampiezza comune di ciascuna di queste parti, consideriamo le seguenti somme:

s_n = m₁h+m₂h+.+m_nh

S_n = M₁h+M₂h+.+M_nh

Ove m_i indica il minimo della f(x) nell' i^mo intervallo, mentre M_i indica il massimo della f(x) nello stesso intervallino.

Quindi è evidente che per un qualunque n risulterà sempre:

s_{n <=} S_n

In pratica il numero s_n rappresenta la somma delle aree degli n rettangoli aventi per base, rispettivamente, gli intervallino in cui è stato diviso l'intervallo [a,b] e per altezze le ordinate minime m_i dei punti della curva in tali intervallino. Mentre il numero S_n rappresenta la somma delle aree degli n rettangoli aventi le stesse basi e per altezze le ordinate massime M_i.

L'insieme dei primi rettangoli costituisce una figura che si chiama plurirettangolo inscritto nel trapezoide; quello dei secondi si chiama plurirettangolo circoscritto. Perciò sommando le aree di queste figure si può approssimativamente risalire a quella del trapezoide, infatti con il punto di minimo ci sarà un approssimazione per difetto, mentre con quello di massimo per eccesso. Per ottenere l'area reale del trapezoide dovremmo aumentare all'infinito il numero degli intervallini, infatti:

lim s_n = lim S_n

^{n n}

si ottiene in questo modo il vero valore dell'integrale definito della f(x) nell'intervallo [a,b]:

_b

f(x) dx

^a

Ovviamente la macchina non può dividere l'intervallo[a,b] in infiniti intervallini più piccoli, perciò dobbiamo approssimare l'area per difetto o per eccesso come detto precedentemente:

_n

s_n = m_{k *} ∆x

^K=1

_n

S_n = m_{k *} ∆x

^K=1

Seconda parte

Il concetto di integrale definito fu dato relativamente ad una funzione continua in un intervallo chiuso. Si presentano però casi in cui le 3 ipotesi che avevamo posto per definire questo tipo di integrale non si avverano, cioè succede che una delle seguenti ipotesi viene a mancare:

1°Hp funzione continua

2°Hp definita in un intervallo chiuso

3°Hp limitata

Perciò è necessario introdurre una nuova tipologia di integrali, quelli impropri.

Se la nostra funzione f(x) non è limitata in un intervallo, ossia esiste almeno un punto X₀ per il quale essa va all'infinito:

lim f(x) =

^{x X0}  

allora l'integrale:

_{b per definizione b}

f(x) dx = lim f(x)dx

^{a c a   c}

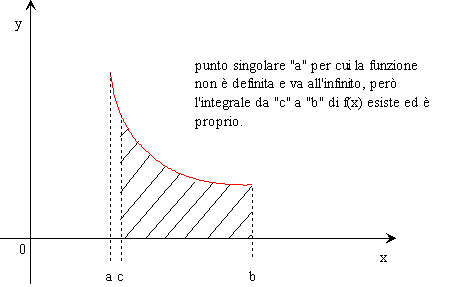
in questo caso parliamo allora di integrali impropri di prima specie e se il limite sopra citato esiste ed è finito, possiamo tranquillamente affermare che l'integrale improprio è convergente o più semplicemente che esiste, oppure che la funzione è integrabile in senso generalizzato. Invece, se facendo il limite risulta allora l'integrale improprio è divergente quindi la funzione non è integrabile.

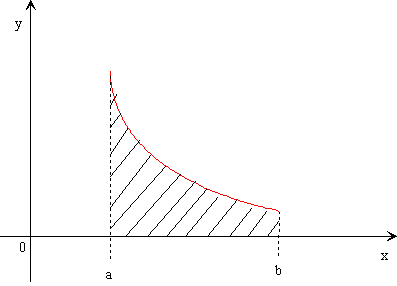
Finora però abbiamo supposto che l'intervallo d'integrazione sia finito. Supponiamo ora che la funzione f(x) sia invece definita su tutto l'intervallo [a,+ ) e sia integrabile nell'intervallo [a,b] per quanto sia grande b, si pone allora per definizione:

_{per definizione b}

f(x) dx = lim f(x)dx

^{a   b a}

In questo caso parliamo di integrali di seconda specie.

Importante per il proseguire dell'esperienza è saper riconoscere velocemente se un integrale improprio converge oppure no servendoci del teorema del confronto, proprio dove questo teorema ha i suoi limiti noi con l'utilizzo del computer cercheremo in un qualche modo di porgli rimedio.

Se abbiamo due funzioni integrandi non negative 

se 0 f(x) g(x) [" x (a,b)]

_b

se g(x) dx è convergente

^a

_b

allora converge pure   f(x) dx

^a

_b

se f(x) dx è divergente

^a

_b

allora diverge pure g(x) dx

^a

I limiti che ha questo teorema però si fanno sentire quando:

_b

se f(x) dx è convergente

^a

_b

allora non possiamo pronunciarci sul carattere di f(x) dx

^a

e viceversa

_b

se s(x) dx è divergente

^a

_b

allora non possiamo pronunciarci sul carattere di f(x) dx.

^a

Gli viene in soccorso però il secondo criterio di convergenza:

lim f(x) =

^{x b} g(x)  

se il risultato di questo limite è un numero finito diverso da 0 allora i due integrali hanno lo stesso carattere,

se è 0, significa che la f(x)<g(x) e si può applicare il 1°criterio del confronto sempre se l'integrale di g(x) converge oppure quello della f(x) diverge,

se è , la g(x)<f(x) e si può applicare se possibile ancora il primo criterio del confronto.

Prove pratiche

Date due funzioni:

f(x) = dx

x

e

g(x) =   dx__

x lnx

ora come richiesto nella 2° parte dell'esperienza proveremo a capire il carattere degli integrali di queste due funzioni, cioè:

_b

dx

^a x

e

_b

_dx__

^a x lnx

analizzandole ci accorgiamo subito che sappiamo già il carattere del integrale della f(x), infatti quest'ultimo avevamo già verificato in classe che divergeva, perciò non ci resta che scoprire il secondo. Quindi visto che conosciamo il carattere di uno degli integrali proviamo ad applicare il primo criterio di convergenza; ci accorgiamo subito però che:

f(x) < g(x)

dx < _dx__

x x lnx

e per quello che abbiamo detto precedentemente nella parte teorica sul 1° criterio di convergenza, non possiamo esprimerci sul carattere dell' integrale della g(x), perché quest'ultima è maggiore della f(x), potremmo ricorrere al secondo criterio di convergenza per dedurlo ma questa esperienza voleva che ci spingessimo oltre. Capire se un computer, tutte le volte che non vale il primo criterio di convergenza riesce a riconoscere il carattere di un integrale.

Perciò ricorriamo all'aiuto del calcolatore; attraverso il programma in linguaggio c++ che abbiamo steso, fissiamo un numero "A" grande a piacere appartenente ad , siamo sicuri che esiste un certo numero p tale che:

_p

dx A

² x

quando "A" vale 1 in corrispondenza di questo valore troviamo il punto "p". Il più piccolo "p" che troviamo che fa valere l' uguaglianza precedente lo prendiamo e lo mettiamo nella tabella specifica costruita per ogni integrale.

_p

dx

^a x

a A p

4.9. 147.679

5.499 243.455

5.9. 401.414

6.49. 661.766

6.9. 1091.06

7.49. 1798.88

8 2966.06

8.5 4980.28

9 8062.94

9.49. 13292.6

9.9. 21915.5

_p

dx

^a lnx *x

a A p

1.4. 22.116

1.69 43.86

1.89. 101.242

2.1 281.516

2.3 981.125

2.5 4509.25

2.7 29053

"A" rappresenta il valore dell'area da ricercare.

Dai dati sperimentali ottenuti si possono fare alcune considerazioni,

nel primo integrale (quello della f(x)) il calcolatore riesce a ricercare il valore della p fino ad un valore dell'area circa pari a 12, mentre nel secondo (quello della g(x)) arriva a mala appena a 2,7, infatti siamo stati costretti addirittura a ridurre gli incrementi dell'area, nel primo erano di 0,5 in 0,5, nel secondo li abbiamo rimpiccioliti a 0,2.

Si nota ancora che, "p" raggiunge molto più velocemente valori elevati nel secondo integrale, dove si aggira già attorno a 30000 quando "A" vale solamente 2,7, mentre nell'integrale precedente la "p" valeva 21915 quando "A" valeva 10.

Da questo deduciamo che il primo integrale (di f(x)) diverge, ed il calcolatore non riesce a calcolare l'area (12) in quanto il numero di cicli che deve compiere è troppo elevato per i tempi a nostra disposizione ovvero, esiste una p, ma è troppo elevata. Il secondo integrale (di g(x)) è convergente, infatti con aree "piccole" (3) il numero di cicli che il calcolatore deve compiere si aggira intorno ai 30000, da cui deduciamo che l'incremento dell'area che abbiamo è infinitesimo, ovvero l'integrale è CONVERGENTE!