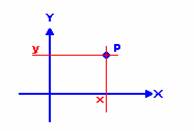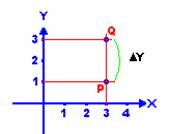
Es. P(3;1) Q(3;3)  d(P;Q)=

2)se il segmento che congiunge i due punti non è parallelo a nessuno dei due assi la distanza si calcola facendo la radice della somma dei quadrati delle differenze dei valori.

Es. P(1;1) Q(5;4) d(P;Q)=

Il punto medio tra due punti è quel punto che giace sulla stessa retta degli altri due e che è equidistante da entrambi. Le coordinate del punto medio sono uguali alla semi somma delle

coordinate dei punti ad esso riferiti.    Es. P(1;1) Q(5;4)  M([1+5]/2;[1+4]/2) M(3;5/2)

Interpretazione geometrica del vettore

Il vettore è un segmento orientato che si indica con una freccia sulla punta. Un vettore può essere definito con tre elementi: MODULO cioè la lunghezza del segmento; DIREZIONE cioè l'inclinazione del segmento stesso; VERSO cioè la parte dalla quale si percorre il segmento.

Due vettori hanno la stessa direzione giacciono su rette parallele. Il vettore, per convenzione, è positivo quando va verso l'alto/destra. Due moduli che hanno stesso modulo stessa direzione ma versi opposti sono opposti. Due vettori sono uguali quando hanno direzione, verso e modulo uguali.

SOMMA DI VETTORI

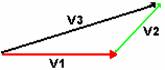
Per sommare due vettori si utilizza il metodo "punta coda" , cioè si fanno coincidere la punta di un vettore con la coda dell'altro. Adesso  si uniscono con un vettore la coda del primo con la punta del secondo e quest'ultimo vettore è la somma dei due vettori iniziali.

Es. V1+V2= V3

DIFFERENZA DI VETTORI

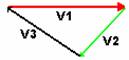
Per sottrarre un vettore ad un altro si utilizza il metodo" punta coda " con la sola differenza che al secondo vettore (sottraendo) bisogna invertire il verso di percorrenza.

Es.  V1-V2= V3

PRODOTTO DI UN VETTORE PER UNO SCALARE

Per moltiplicare un vettore V1 di origine in O  e di punta P(x;Y) per uno scalare n si moltiplicano entrambe le coordinate del punto P per lo scalare n. Fatto ciò otterremo un vettore V2 di origine in O e di punta P1(nx;ny).

Funzioni e Relazioni

Una relazione o grafico è una figura disegnata sul piano cartesiano e caratterizzata dalla possibilità che ad ogni valore sull'asse delle X possa corrispondere più di un valore dell'asse delle Y. Ogni relazione ha una equazione matematica che la descrive.

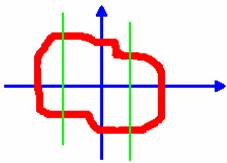
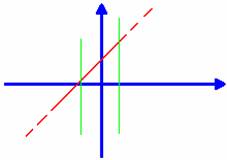
Una funzione è una curva disegnata sul piano cartesiano e caratterizzata dalla presenza per ogni valore della x un solo valore delle y tranne nel caso di retta parallela all'asse delle Y dove i punti corrispondenti ad un solo punto delle x sono infiniti.

Rette Parallele, Perpendicolari e Incidenti

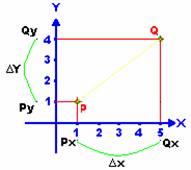
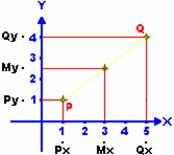
Il rapporto tra variazione delle Y(Dy) e variazione delle X(Dx) prende il nome di coefficiente angolare(m) o pendenza.

Il coefficiente angolare m è espresso nell'equazione esplicita della retta nome coefficiente della X quindi l'equazione generica può essere espressa cosi:  y = mx + q ; dove q è il termine noto dell'equazione e nel grafico viene rappresentato con il punto della retta che ha ascissa uguale a 0.

Osservando l'equazione esplicita di una retta, ma soprattutto dal suo coefficiente angolare possiamo distinguere quattro diversi casi:

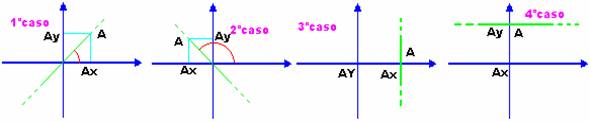
1°caso: se Dy e Dx  hanno segni concordi allora m > 0 e quindi la retta formerà un angolo acuto con l'asse delle x

2°caso: se Dy e Dx  hanno segni discordi allora m < 0 e quindi la retta formerà un angolo ottuso con l'asse delle x

3°caso: se Dy è uguale a zero allora m = 0 e quindi la retta sarà parallela all'asse delle Y

4°caso: se Dx è uguale a zero allora m = e quindi la retta sarà parallela all'asse delle X