Funzioni di 1° grado

matematica

Funzioni di 1° grado

y = mx + q

m = -a/b = pendenza della retta = aumenta con l'aumentare di y

q = -c/b = distanza dall'origine = intersezione della retta con l'asse delle 929f57j y

La retta passante per un punto

y - y₀ = m(x-x₀)

La retta passante per due punti

(y-y₁)/(y-y₂) = (x-x₁)/(x₂-x₁)

La retta passante per tre punti

(y₃-y₁)/(y-y₂) = (x₃-x₁)/(x₂-x₁)

La retta parallela ad un'altra retta

y = mx + k (esplicita)

ax+by+k=0 (implicita)

se parallela all'asse delle x : y = k a=0 m=0

se parallela all'asse delle y : x = h b=0

La retta perpendicolare ad un'altra

y = -1/m*x + k (esplicita)

bx - ay + k = 0 (implicita)

Bisettrice dei quadranti

I e III quadrante: y=x

II e IV quadrante: y=-x

Distanza tra un punto e una retta:

d: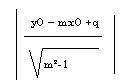

Forma segmentaria della retta

x/p + y/q = 1

Intersezione di due rette

Faccio il sistema con le equazioni di entrambe le rette. Quindi sostituisco.

Appartenenza di un punto alla retta

Applico la formula y = mx + q sostituendo a x e y le coordinate del punto.