 |  | |
|
| | |
|
| |
Matematica
Differenziale di una funzione
Il differenziale di una funzione y = f(X) in un punto in cui la funzione è derivabile è il prodotto tra la derivata alla funzione stessa in quel punto e l'incremento della variabile indipendente
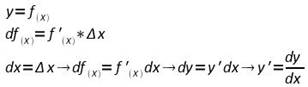
si usa nella risoluzione delle funzioni differenziali
Integrali
Indefiniti
Definizione:
Data una funzione y = f(x) continua si dice integrale indefinito della funzione data la totalità delle sue primitive, ovvero la famiglia di funzioni (differenti per una costante K) che hanno come derivata la funzione stessa.
Proprietà:
L'integrale della somma di due funzioni nella stessa variabile è uguale alla somma delle integrali delle due funzioni
Una costante moltiplicativa può sempre essere portata dentro o fuori dall'integrale
L'operazione di integrale è quindi lineare e le due proprietà sopra descritte valgono anche insieme
Risoluzione:
Integrali immediati
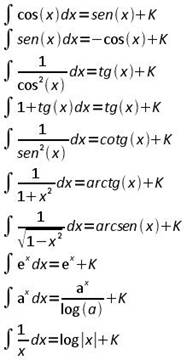
Integrazione immediata di funzioni composte
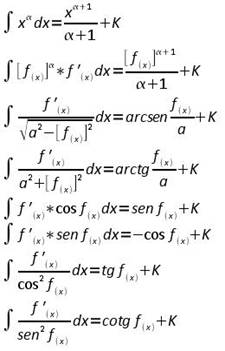
Metodo della scomposizione
Quando è possibile si scompone un'unica funzione nella somma di funzioni integrabili con le formule relative alla funzione data
Metodo dell'integrazione per parti
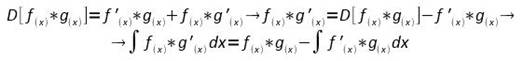
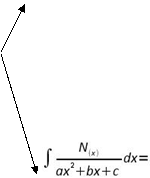
Schema riassuntivo dell'integrazione di funzioni razionali fratte
grado N(X) > grado D(X)
∆
> 0
potenza...
∆ < 0
Definiti
Definizione:
C
D
ST = ?
Weiestrass
y = f(X) continua in [a ; b] 
m , M; ∆x
somma int. inf.
sn = ∆xm1
+ ∆xm2 + ... = =
somma int..sup.
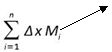
Sn = ∆xM1 + ∆xM2 + ... = =
Data una funzione f(X) continua in [a ; b] , si chiama integrale definito il valore comune del limite per n della sn e della Sn
Le successioni delle somme integrali inferiori e superiori relative a una funzione f(X) continua nell'intervallo chiuso e limitato [a ; b] sono convergenti e ammettono per n lo stesso limite finito.
Questo limite finito si chiama integrale definito di f(X) in [a; b] e si indica come ; L'integrale definito avrà come risultato sempre un numero. In particolare:
f(X) > 0 = S (>0) = SABCD
f(X) < 0 = S (<0) = non area
<
f(X)
0 = Somma
algebrica delle aree positive e negative
Proprietà
per y = f(X) continua in [a ; b]
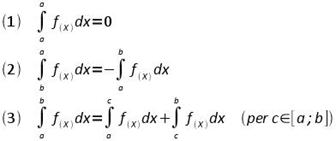
Anche per i definiti sono valide le proprietà degli integrali indefiniti.
Teorema della media:
Data la funzione y = f(X)
continua in [a ; b] esiste all'interno dell'intervallo [a ; b] un punto c per
il quale
= (b - a) ∙ f(C)
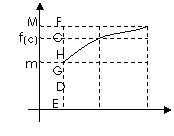Dimostrazione (f(X) > 0)
y = f(X) continua in [a ; b] m , M RABED < TABCD < RABCF
(b-a) ∙ m < < (b-a) ∙ M f(C) per Darboux
f(C) = valore medio della funzione
Geometricamente il teorema della media dice che l'area del trapezoide è equivalente a quella di un rettangolo con base AB e per altezza il valore medio f(C).
Teorema del calcolo di Torricelli
Dimostrazione
Se la funzione y = f(X) è continua nell'intervallo chiuso e limitato [a;b] la corrispondente funzione integrale F(X) è derivabile per ogni x appartenente ad [a;b] e quindi
F'(X) = f(X)
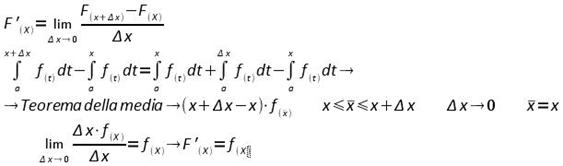
Conseguenza:
L'integrale definito di una funzione è uguale alla differenza dei valori assunti da una qualsiasi delle sue primitive rispettivamente nell'estremo superiore e in quello inferiore di integrazione
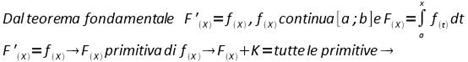
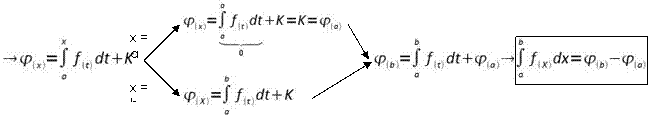
Area di una superficie piana mistilinea
f(X), g(X) continue in [a ; b] f(X) > g(X)
Volume di solidi di rotazione
f(X)) continua in [a ; b]
Integrali impropri o generalizzati
- un estremo = l converge diverge
indeterminato
nell'estremo b la funzione è discontinua
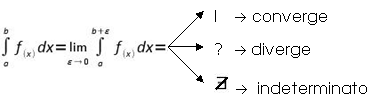
Equazioni differenziali
Un'equazione differenziale è un'equazione matematica dove figurano la variabile indipendente x, la funzione incognita y ed alcune sue derivate.
Una equazione differenziale è detta di ordine n quando n è l'ordine massimo delle derivate presenti.
Soluzione o integrale di un'equazione differenziale è una funzione che la soddisfa e il grafico si chiama curva integrale.
Le soluzioni generali sono infinite e dipendono un numero di variabili pari all'ordine n dell'equazione differenziale.
Per avere la soluzione particolare si deve specificare la K imponendo delle condizioni iniziali (generalmente coordinate di un punto per il quale debba passare la curva integrale).
Risoluzione di equazioni differenziali del 1° ordine (a variabili separabili o lineari)
A variabili separabili:
Si sostituisce con , si separano le variabili mettendone una a primo membro e una a secondo membro e si
calcola l'integrale nelle due variabili separate.
Lineari
Un'equazione differenziale si dice lineare quando la y e la y' sono del primo grado.
Il modello di riferimento è questo:
b(X) = 0 l'equazione è omogenea
formula risolutiva:
b(X) l'equazione è completa
formula risolutiva:
Serie numeriche
Una successione numerica è una particolare funzione che assegna ad un numero naturale un numero reale
f:N R
Viene così a generarsi un insieme dove n indica il posto occupato da An in questo insieme. An è il termine generale.
PROBLEMA: la somma dei termini di una successione è la somma di infiniti termini. Come fare per "calcolarla"?
Questo problema è risolto dalla teoria delle serie numeriche.
Serie numerica: la somma degli infiniti termini di una successione numerica
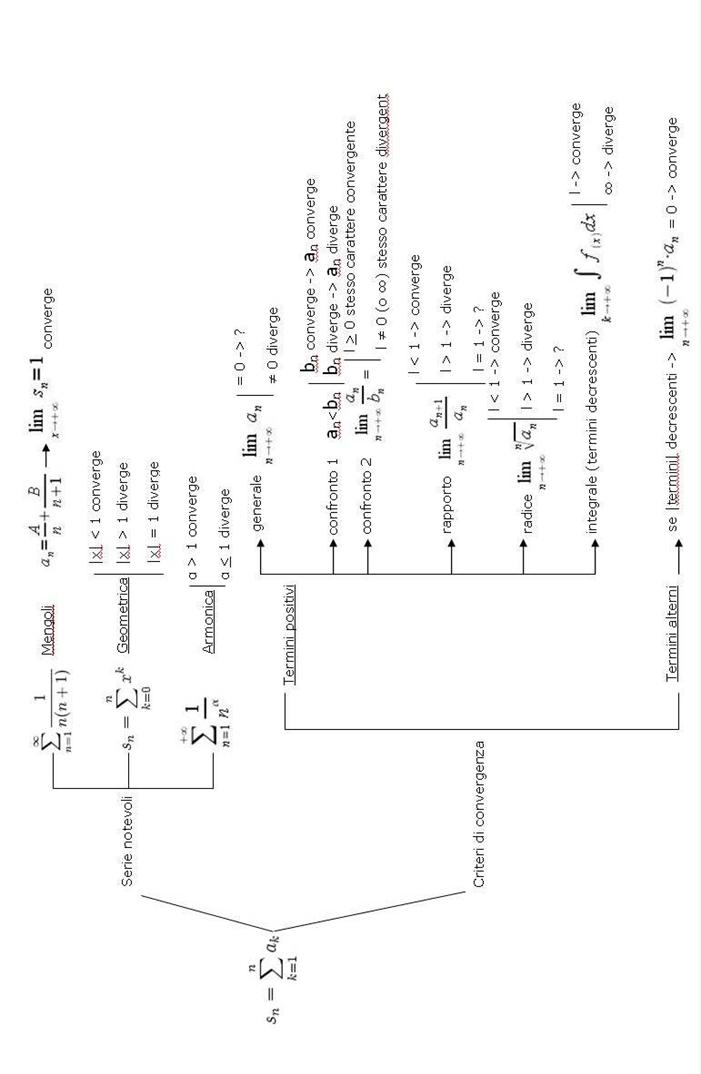
Studiare il carattere di una serie significa studiare se una serie è convergente, divergente o indeterminata.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025
