|
|
| |
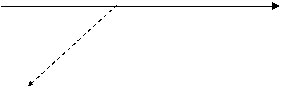
Una persona cammina seguendo questo percorso: 3,1Km verso nord, poi 2,4Km verso ovest ed infine 5,2Km verso sud.
Costruire il diagramma vettoriale che rappresenta questo moto.
Quale distanza dovrebbe percorrere, ed in quale direzione, un uccello che voli in linea retta per raggiungere lo stesso punto di arrivo ?
SVOLGIMENTO
Fissiamo un sistema di riferimento bidimensionale in modo tale da far coincidere l'origine degli assi con il punto A di partenza del percorso:
![]() y
y
![]()
![]()
![]() C B
C B
A x
D
Dai dati del problema si ha:
![]()
![]()
![]()
![]()
![]()
![]() AB = 3,1 j BC
= -2,4 i CD = -5,2 j
AB = 3,1 j BC
= -2,4 i CD = -5,2 j
![]()
Il vettore AD è dato da:
![]()
![]()
![]()
AD = ADx + ADy
![]()
![]()
![]() dove ADx = (ABx + BCx + CDx) i = -2,4 i
dove ADx = (ABx + BCx + CDx) i = -2,4 i
![]()
![]()
![]() ADy = (ABy + BCy + CDy) j = -2,1 j
ADy = (ABy + BCy + CDy) j = -2,1 j
![]()
![]()
![]() Quindi
AD = -2,4 i -2,1 j
Quindi
AD = -2,4 i -2,1 j
![]()
![]()
![]() AD = (ADx + (ADy = 10,17 = 3,2 Km
AD = (ADx + (ADy = 10,17 = 3,2 Km
La direzione si ricava da:
ADy
![]() tgj =
0,875
tgj =
0,875
ADx
da cui j = 221° rispetto all'orizzontale.
ESERCIZIO N° 2
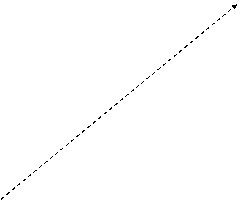
Un'automobile viaggia per 50Km in direzione est, poi per 30Km in direzione nord e poi per 25Km in una direzione nord-est a 30° rispetto al nord.
Tracciare il diagramma vettoriale.
Determinare lo spostamento totale compiuto dall'automobile dal suo punto di partenza.
SVOLGIMENTO
Scegliamo un sistema di riferimento bidimensionale in modo tale da far coincidere l'origine degli assi con il punto A di partenza:
![]()
![]() y
y
 D
D
![]()
![]() 30°
30°
C
![]() j
j
![]()
![]() A B x
A B x
Dai dati del problema si ha:
![]()
![]() AB = (50Km)
i
AB = (50Km)
i
![]()
![]() BC = (30Km)
j
BC = (30Km)
j
![]()
![]()
![]()
![]()
![]() CD = [25sen(30°)] i + [25cos(30°)] j = 12,5 i + 21,65 j
CD = [25sen(30°)] i + [25cos(30°)] j = 12,5 i + 21,65 j
![]() Il
vettore AD è dato da:
Il
vettore AD è dato da:
![]()
![]()
![]() AD = ADx + ADy
AD = ADx + ADy
![]()
![]()
![]()
![]() dove ADx = (ABx + BCx + CDx) i = (50 + 12,5) i = 62,5 i
dove ADx = (ABx + BCx + CDx) i = (50 + 12,5) i = 62,5 i
![]()
![]()
![]()
![]() ADy = (ABy + BCy + CDy) j = (30 + 21,65) j = 51,65 j
ADy = (ABy + BCy + CDy) j = (30 + 21,65) j = 51,65 j
![]()
![]()
![]() Quindi
AD = 62,5 i + 51,65 j
Quindi
AD = 62,5 i + 51,65 j
![]()
AD = (ADx + (ADy = 81 Km
Per la direzione
ADy
![]() j = arctg
= 40°
j = arctg
= 40°
ADx
ESERCIZIO N° 3
Un giocatore di golf in tre colpi riesce a mandare la sua palla nella buca. Il primo colpo sposta la palla di 12m verso nord, il secondo di 6m in direzione sud-est ed il terzo colpo di 3m in direzione sud-ovest.
Quale spostamento sarebbe stato necessario per mandare la palla nella buca al primo colpo ?
SVOLGIMENTO
Fissiamo un sistema di riferimento bidimensionale in cui l'origine degli assi coincida col punto di partenza:
![]() y
y

![]() B
B
![]()
C
![]() D
D
![]() j
j
![]() x
x
A
Lo spostamento necessario per mandare la palla in buca al primo colpo è rappresentato dal vettore:
![]()
![]()
![]() AD = ADx + ADy
AD = ADx + ADy
![]()
![]()
![]()
![]()
![]() dove ADx = (ABx + BCx + CDx) i
dove ADx = (ABx + BCx + CDx) i
![]()
![]()
![]()
![]()
![]() ADy = (ABy + BCy + CDy) j
ADy = (ABy + BCy + CDy) j
Dai dati del problema si ottiene:
![]()
![]() AB = 12 j
AB = 12 j
![]()
![]()
![]()
![]()
![]() BC =
6cos(45°) i - 6 sen(45°) j = 4,24 i - 4,24 j
BC =
6cos(45°) i - 6 sen(45°) j = 4,24 i - 4,24 j
![]()
![]()
![]()
![]()
![]() CD =
-3cos(45°) i -3sen(45°) j = -2,12 i -2,12 j
CD =
-3cos(45°) i -3sen(45°) j = -2,12 i -2,12 j
Da ciò si ricava:
![]()
![]()
![]() AD =
2,12 i + 5,64 j
AD =
2,12 i + 5,64 j
![]()
AD = (ADx + (ADy = 6m
Per la direzione:
ADy
![]() j = arctg
= 70° rispetto all'orizzontale.
j = arctg
= 70° rispetto all'orizzontale.
ADx
ESERCIZIO N° 4
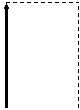
Un uomo desidera raggiungere una località situata a 3,4Km di distanza dal luogo dove attualmente si trova, in direzione nord-est con un angolo di 35° rispetto a nord. Egli si trova costretto però a percorrere strade che possono avere solo due direzioni: o nord-sud, oppure est-ovest. Qual è la minima distanza che l'uomo dovrebbe percorrere per raggiungere la destinazione ?
Indichiamo con A il punto di partenza e con B quello di arrivo.
Fissiamo un sistema di riferimento bidimensionale in modo tale da far coincidere l'origine degli assi col punto A di partenza
![]() y
y
 B
B
![]()
ABy
![]()
![]() ABx
ABx
![]()
![]() x
x
![]()
Il vettore AB (spostamento totale) può essere scomposto nella somma dei due suoi vettori componenti lungo i due assi, cioè:
![]()
![]()
![]()
AB = ABx + ABy
La minima distanza d sarà allora data dalla somma dei moduli dei due vettori componenti:
d = ABx + ABy = ABsen(35°) + ABcos(35°) = 3,4∙0,57 + 3,4∙0,82 = 4,72Km
ESERCIZIO N° 5
![]()
![]() Due
vettori a e b hanno lo stesso modulo di 10 unità. Essi sono orientati come in
figura:
Due
vettori a e b hanno lo stesso modulo di 10 unità. Essi sono orientati come in
figura:
![]() y
y

![]() b 105°
b 105°
![]()
![]()

![]() a
a
![]()
![]() 30°
30°
x
Trovare:
a)
![]() le
componenti del loro risultante r secondo i due assi x e y;
le
componenti del loro risultante r secondo i due assi x e y;
b)
![]() il
modulo di r ;
il
modulo di r ;
c)
![]() l'angolo
j che r forma con l'asse x.
l'angolo
j che r forma con l'asse x.
Si ha, per le componenti:
![]()
![]()
![]()
![]()
![]() r = a +
b = rx i + ry j
r = a +
b = rx i + ry j
rx = ax + bx = a∙cos(30°) + b∙cos(135°) = 1,59
ry = ay + by = a∙sen(30°) + b∙sen(135°) = 12,07
Per il modulo
![]()
r = (rx + (ry = 12,17
Per l'angolazione
ry
![]() j = arctg =
82,5° rispetto all'orizzontale.
j = arctg =
82,5° rispetto all'orizzontale.
rx
ESERCIZIO N° 6
Tre vettori sono dati da:
![]()
![]()
![]()
![]()
![]() A = 3 i + 3 j -2 k
A = 3 i + 3 j -2 k
![]()
![]()
![]() B = -i -4
j +2 k
B = -i -4
j +2 k
![]()
![]()
![]()
![]() C = 2 i + 2 j + k
C = 2 i + 2 j + k
Trovare:
![]()
![]()
![]()
a) A∙(B x C)
b)
![]()
![]()
![]() A∙(B
+ C)
A∙(B
+ C)
c)
![]()
![]()
![]() A x (B +
C)
A x (B +
C)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Ricordiamo
che dati due vettori A = Axi + Ayj + Azk e B = Bxi + Byj + Bzk allora risulta:
Ricordiamo
che dati due vettori A = Axi + Ayj + Azk e B = Bxi + Byj + Bzk allora risulta:
![]()
![]()
A∙B = AxBx + AyBy + AzBz
e
![]()
![]()
![]()
![]()
![]() A x B = i(AyBz - AzBy) + j(AzBx - AxBz) + k(AxBy - AyBx
A x B = i(AyBz - AzBy) + j(AzBx - AxBz) + k(AxBy - AyBx
![]()
![]() Quindi
per rispondere al quesito a) ricaviamoci prima B x C:
Quindi
per rispondere al quesito a) ricaviamoci prima B x C:
![]()
![]()
![]()
![]()
![]() B x C =
-8 i + 5 j + 6 k
B x C =
-8 i + 5 j + 6 k
![]()
![]()
![]() Posto
ora B x C = D si ottiene:
Posto
ora B x C = D si ottiene:
![]()
![]() A∙D = AxDx + AyDy + AzDz
A∙D = AxDx + AyDy + AzDz
Per il quesito b):
![]()
![]()
![]()
![]()
![]() B + C = i -2
j + 3 k
B + C = i -2
j + 3 k
e quindi
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() A x D = i(AyDz - AzDy) + j(AzDx - AxDz) + k(AxDy - AyDx) = 5 i -11 j -9 k
A x D = i(AyDz - AzDy) + j(AzDx - AxDz) + k(AxDy - AyDx) = 5 i -11 j -9 k
ESERCIZIO N° 7
Un vettore ha modulo unitario (versore); gli angoli che esso forma con i tre assi x, y, z di una terna cartesiana ortogonale sono tra loro uguali.
Trovare i coseni direttori della direzione del vettore.
Trovare le componenti cartesiane del vettore.
![]() u (cosa , cosb , cosg
u (cosa , cosb , cosg
![]()
![]()
![]() Siano inoltre i,
j, k i versori degli assi x, y, z, i cui coseni
direttori sono
Siano inoltre i,
j, k i versori degli assi x, y, z, i cui coseni
direttori sono
![]() i
i
![]() j
j
![]() k
k
Si ha allora
![]()
![]() u ∙ i = cosa
u ∙ i = cosa
![]()
![]() u ∙ j = cosb
u ∙ j = cosb
![]()
![]() u ∙ k = cosg
u ∙ k = cosg
![]() Poiché
gli angoli formati dalla direzione di u con gli assi sono uguali, abbiamo
Poiché
gli angoli formati dalla direzione di u con gli assi sono uguali, abbiamo
cosa = cosb = cosg
La proprietà di ortogonalità dei coseni direttori
cos a + cos b + cos g
diventa dunque
3cos a
da cui deriva
![]()
![]() cosa
cosa
![]()
![]()
![]()
![]() Due
vettori a e b hanno come componenti a (1,1,1) , b (1,0,1). Calcolare
Due
vettori a e b hanno come componenti a (1,1,1) , b (1,0,1). Calcolare
il modulo di ciascun vettore;
il prodotto scalare tra i due vettori;
l'angolo formato dai due vettori.
Poiché il modulo di un vettore è dato da:
![]()
v = vx + vy + vz
allora
![]()
![]()
a = 3 b = 2
Il prodotto scalare fra i due vettori è
![]()
![]() a ∙
b = axbx + ayby + azbz
a ∙
b = axbx + ayby + azbz
Per conoscere l'angolo formato dai due vettori possiamo utilizzare la definizione di prodotto scalare tra due vettori:
![]()
![]() a
∙ b = abcosj
a
∙ b = abcosj
da cui
![]()
![]() a ∙ b 2
a ∙ b 2
![]()
![]()
![]() cosj = = 0,816
cosj = = 0,816
ab 6
Da ciò si ottiene quindi:
j
che espresso in radianti sarebbe:
j = 0,616 rad.
ESERCIZIO N° 9
![]()
![]()
![]()
![]() Due
vettori a e b hanno come componenti a (1,1,1) , b
Due
vettori a e b hanno come componenti a (1,1,1) , b
Detto c il prodotto vettoriale fra i due vettori, trovare:
![]() Le
componenti cartesiane di c.
Le
componenti cartesiane di c.
![]() Il
modulo di c.
Il
modulo di c.
![]()
![]() L'angolo
fra i due vettori a e b.
L'angolo
fra i due vettori a e b.
Il prodotto vettoriale di due vettori può essere scritto in termini delle componenti dei due vettori nel seguente modo:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() c = a X b = ( i ax + j ay+ k az X ( i bx + j by+ k bz ) = i (aybz - azby) + j (azbx - axbz) + k (axby - aybz
c = a X b = ( i ax + j ay+ k az X ( i bx + j by+ k bz ) = i (aybz - azby) + j (azbx - axbz) + k (axby - aybz
![]() Le
componenti cartesiane di c risultano quindi
Le
componenti cartesiane di c risultano quindi
cx
cy
cz
![]()
![]()
c cx + cy + cz =
Con la stessa formula calcoliamoci a e b per poter determinare l'angolo tra i due vettori.
![]()
![]() a = 3 b
= 5
a = 3 b
= 5
Poiché
c = absenj
allora
![]() c 6
c 6
![]()
![]()
![]() j = arcsen =
arcsen = 0,684 rad.
j = arcsen =
arcsen = 0,684 rad.
ab 15
ESERCIZIO N° 10
Rispetto ad un sistema di assi cartesiani ortogonali Oxyz un punto P ha coordinate P (1,1,3) mentre una retta r ha coseni direttori a b g. Trovare
![]()
modulo e componenti cartesiane del vettore OP;
![]() le
componenti di OP lungo la retta r e
nel piano perpendicolare a tale retta.
le
componenti di OP lungo la retta r e
nel piano perpendicolare a tale retta.
![]()
Le componenti cartesiane del vettore OP coincidono con le coordinate di P. Quindi
![]()
![]() Il
modulo di questo vettore è OP = 11
Il
modulo di questo vettore è OP = 11
![]()
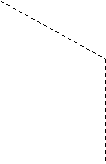
![]() Indicato
con u un versore orientato come la retta r,
le componenti di u sono i coseni direttori della retta, si ha cioè
Indicato
con u un versore orientato come la retta r,
le componenti di u sono i coseni direttori della retta, si ha cioè
![]() u a b g
u a b g

![]() r
r
![]() OPn
OPn
![]() OPr
OPr
P
 O
O
![]() La
componente OPr di OP lungo
la retta r è data da
La
componente OPr di OP lungo
la retta r è data da
![]()
![]() OPr = OP ∙ u
= a b g
OPr = OP ∙ u
= a b g
![]()
Il vettore OP risulta così decomposto in un componente OPr parallelo alla retta r ed in uno, OPn, normale alla stessa. Per il teorema di Pitagora:
OPr + OPn = OP
La componente OPn è data quindi da
![]()
OPn = 11 - (a b g
ESERCIZIO N° 11
![]()
![]()
![]()
![]()
![]()
![]() Tre
vettori a, b, c hanno le seguenti componenti a (1,2,1)
, b (2,4,0)
, c
Tre
vettori a, b, c hanno le seguenti componenti a (1,2,1)
, b (2,4,0)
, c
![]()
![]()
![]() Provare
che il modulo del prodotto a ∙ b X c è il volume del parallelepipedo avente come
spigoli i tre vettori.
Provare
che il modulo del prodotto a ∙ b X c è il volume del parallelepipedo avente come
spigoli i tre vettori.
Esprimere in forma cartesiana tale prodotto.
Mostrare che esso è esprimibile per mezzo di un determinante.
Calcolare tale prodotto nel caso particolare suggerito giustificando a posteriori il risultato ottenuto.
![]()
![]()
![]()
![]()
![]() Il
prodotto vettoriale b X c dà come
risultato un vettore d perpendicolare al piano dei due vettori avente come
modulo d = bcsenq, essendo q l'angolo formato dai due vettori b e c.
Il
prodotto vettoriale b X c dà come
risultato un vettore d perpendicolare al piano dei due vettori avente come
modulo d = bcsenq, essendo q l'angolo formato dai due vettori b e c.
Ma si ha che csenq è l'altezza DH del parallelogramma costruito sui due vettori:
D C![]()
![]()
![]()
![]()
![]() c
c
![]()
![]() q b
q b
![]() A H B
A H B
Il modulo bcsenq è quindi l'area di tale parallelogramma.
Il prodotto scalare
![]()
![]() a
∙ d = adcosj
a
∙ d = adcosj
![]()
![]() essendo j l'angolo formato da a col vettore d
essendo j l'angolo formato da a col vettore d
![]()
![]() d
d
![]()
![]()
![]() a
a
acosj
 j
j
![]()
![]() c
c
![]() b
b
![]()
![]()
![]() Poiché
acosj è la proiezione del vettore a sulla
normale al piano individuato da b e da c, esso rappresenta l'altezza del
parallelepipedo avente come spigoli i tre vettori. Ne segue dunque che il
prodotto misto tra i tre vettori esprime il volume del parallelepipedo stesso.
Poiché
acosj è la proiezione del vettore a sulla
normale al piano individuato da b e da c, esso rappresenta l'altezza del
parallelepipedo avente come spigoli i tre vettori. Ne segue dunque che il
prodotto misto tra i tre vettori esprime il volume del parallelepipedo stesso.
![]()
![]() Il
prodotto vettoriale b X c può essere
scritto come
Il
prodotto vettoriale b X c può essere
scritto come
![]()
![]()
![]() i (bycz - bzcy) + j (bzcx - bxcz) + k (bxcy - bycz
i (bycz - bzcy) + j (bzcx - bxcz) + k (bxcy - bycz
![]() I
coefficienti dei versori rappresentano le componenti cartesiane del vettore d e
quindi:
I
coefficienti dei versori rappresentano le componenti cartesiane del vettore d e
quindi:
![]()
![]() a
∙ d = ax(bycz - bzcy) + ay(bzcx - bxcz) + az(bxcy - bycz
a
∙ d = ax(bycz - bzcy) + ay(bzcx - bxcz) + az(bxcy - bycz
Ma tale uguaglianza coincide proprio con il seguente determinante
![]()
![]() ax ay az
ax ay az
bx by bz
cx cy cz
![]()
![]() 1 2 1
1 2 1
![]()
![]()
![]() a
∙ b X c = 2 4 0 = 0
a
∙ b X c = 2 4 0 = 0
3 6 1
Il volume del parallelepipedo costruito sui tre vettori è nullo, come poteva ricavarsi osservando che i tre vettori giacciono in un piano.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025