Proprietà del campo elettrico. Lavoro, potenziale, energia potenziale.

fisica

Proprietà del campo elettrico. Lavoro, potenziale, energia potenziale.

3.1 Potenziale del campo

La proprietà del campo elettrico è di essere conservativo.

Si può esprimere tale proprietà:

a) 242f52c   Esiste una funzione scalare V(x,y,z), detta POTENZIALE del CAMPO tale che:

  

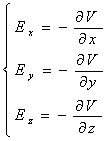
(4)

dove:

Può essere utile esprimere il potenziale in funzione della coordinata curvilinea s, V(s), tale che:

  (5)

= componente di lungo la curva .

b) 242f52c   Il lavoro delle forze del campo su di una carica per spostarla da A a B lungo una linea non

dipende dal cammino ma solo dagli estremi.

da cui:

sostituendo la (5):

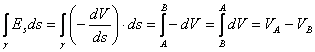
in definitiva:

(6)

(Volt)

Il lavoro che un campo conservativo compie su una carica q  per spostarla da non dipende dal cammino , ma dal valore cha la funzione potenziale assume negli estremi A e B (cambiata di segno).

Se risulta:

il lavoro risulta nullo lungo chiuso (7)

Dalla (6):

(8)

dove U = energia potenziale di q nel campo conservativo.

Infatti l'energia totale di una particella di massa m, carica q vale:

Se la particella subisce una variazione di velocità, da a , da uno stato di potenziale a quello di potenziale (calcolati rispetto lo stesso potenziale di riferimento) si può scrivere:

per la conservazione dell'energia totale:

ma il primo termine è il lavoro, pertanto:

variazione energia potenziale

3.2 Lavoro positivo e lavoro negativo.

Il lavoro risulta positivo se:

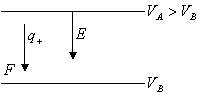
concorde al campo

si ha aumento di energia cinetica. È il campo che lavora.

Il lavoro risulta negativo se:

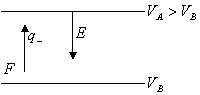
discorde al campo

In questo caso per far scendere la carica si deve applicare una forza dall'esterno contro il campo.

3.3 Definizione di elettronvolt (eV)

Uno ione fermo acquista energia cinetica in un campo creato da una differenza di potenziale pari a:

Si definisce ELETTRONVOLT l'energia acquisita da un elettrone in =1 Volt e vale: