FISICA SPERIMENTALE B - ELETTROSTATICA

Campo elettrico esiste indipendentemente dalla carica Q di prova:

E = F/Q = 1/4πε_o q/r² (vel. di propagazione campo = vel. luce)

Cariche non puntiformi

ρ = Q/Volume = densità di carica

E = 1/4πε_o · ∫_V ρ/r² dv

Proporzione tra F gravitazionale e F elettrostatica

F_el / F_g = 10⁴³ posso ignorare F_g

Proprietà della carica elettrica 1) conservazione della carica totale

2) quantizzazione della carica: dq = ρ dv non è infinitesima, la carica minima è l'elettrone e 151i85b il protone

Lavoro del campo elettrostatico (E è conservativo, quindi L non dipende da traiettoria)

L = ∫F ds = q₁q₂/4πε_o · (1/r_b - 1/r_a)

Energia potenziale L per portare carica da r_b = ∞ a r_a

Ep = 1/4πε_o · q₁q₂/r

Potenziale elettrostatico

V = Ep/Q = 1/4πε_o q/r L = Q (V_A - V_B) = -QΔV

V = Σ V_i E_x,y,z = - ∂V/∂x,y,z · dx,dy,dz E = - ΛV

con Λ = vettore derivate parziali

dV = -E · dl

Legge di Gauss Φ_E = ∫ E n dΣ = Q_{contenuta in Σ} / ε_o

Flusso generato da guscio sferico carico

Φ_E = Q/ε_o = E Σ E = Q/Σ 1/ε_o = σ/ε_o

all'interno di un conduttore non c'è campo, poiché Q interno a Σ è 0

Cariche sferiche: ext: E = Q/A 1/ε_o = Q/4πε_or² ÷ 1/r²

int: E = Qint/A 1/ _o (Qint = ρ 4/3 r³, A = 4 r²)

E = (ρ 4/3 r³) / 4 _or² = _o r/3   ÷ r

Cariche superficiali piane considero piano infinito carico:

E = ½ σ/ε_o u_n

E è costante e non dipende dalla distanza (poiché il piano è infinito)

Cariche cilindriche: considero un cilindro infinito carico:

ext: E = ρ/ε_o · R²/r ÷1/r

int: E = ρ/ε_o · 2r ÷ r

Cariche filiformi considero filo infinito carico:

E = λ / 2πε_od

Cariche ad anello considero solo E lungo la retta passante per il centro dell'anello:

E = λhR / 2ε_o(h²+R²)^3/2

Energia elettrostatica

dW = V dq W = ∫V dq

esempio: caricare una sfera:

V = 1/4πε_o q/r q = ρ 4/3 π r³ V = ρr²/3ε_o

dq = r² dr)(=d Vol)

W = ∫ V dq = ∫ r²/3 _o r² dr = 4π/3ε_o ρ² ∫ r⁴ dr = 4π/3ε_o ρ²R⁵/5

W sostituisco = q / 4/3 R³ = 3/5 Q/4 _o 1/R

Conduttori e isolanti

Un materiale conduttore immerso in un campo elettrostatico subisce l'effetto dell'induzione elettrostatica, detta completa se tutte le linee di campo passano per il conduttore. All'interno del conduttore il campo è nullo, le cariche si dispongono sulla superficie e generano un campo esterno che nei pressi della superficie è perpendicolare ad esse, poiché altrimenti vi sarebbe una componente di E tangente che farebbe muovere le cariche.

Teorema di Coulomb E = ρ/ε_o

Condensatori: E uniforme = ρ/ε_o     V = ρ d / ε_o = q/ε_o d/A = E d

C = _o A/d = q/V u.m.: Farad = C/V

energia associata a E: W = ½ Q²/C = ½ V²C = ½ VQ = ½ E²ε_o Ad (Ad = vol)

esempio se V = sfera:   W = ∫(_4/3 πr³) ½ E²ε_o dv = ∫₀^R ½ ε_o (1/4πε_o)² Q²/R⁴ 4πr² dr

(dv = 4πr² dr)

Condensatore cilindrico: E = σ/ε_o a/l V = -q/2 ε_ol log(b/a)

C = q/ V = 2 ε_ol / log(b/a)

Condensatore sferico: C = 4 ε_o / (1/a - 1/b)

Corrente elettrica I = dQ/dt = ∫_Σ J · n dΣ con J = densità di corrente = q N v

Q = v · n t con n = normale alla superficie, v = velocità

I = q N v n Σ = ∫_Σ J n dΣ N = n portatori di q / Volume

Corrente in un metallo V = R I R = resistenza u.m.: Ω Ohm

R = · L_unghezza/S_uperficie = resistività ~ T u.m.: Ω/m

Campo conservativo: carica: puntiforme o sferica: circuitazione = ∫_A^A qE · dl = 0

Forza elettromotrice:G = differenza di potenziale ai morsetti del generatore a circuito aperto. nel generatore è presente una resistenza interna r tale per cui:

G = RI + rI

Resistenze in serie R_tot = R₁ + R₂ V_tot = V₁ + V₂ I = cost

in parallelo: 1/R_tot = 1/R₁ + 1/R₂ V = cost I_tot = I₁ + I₂

Legge alle maglie: Σ_A^A V_i = 0

ai nodi: Σ_A^A I = 0

Divergenza di E: data una superficie gaussiana Σ che racchiude un volume V,

dwE = lim _{Σ>>0 ovvero V>>0} Φ_E/V

dwE = ∂E_x/∂x + ∂E_y/∂y + ∂E_z/∂z = ΛE con Λ = vettore derivate parziali

Φ_E = [ ∂E_x/∂x + ∂E_y/∂y + ∂E_z/∂z ] dx dy dz = dwE dx dy dz

teorema di gauss: Φ_E = ∫_Vol ΛE dV

dwE = ρ/ε_o (se E è solenoidale dwE = 0)

equazione di poisson:   E = -ΛV ΛE = ρ/ε_o = Λ(-ΛV) Λ²V = -ρ/ε_o

Rotore di E: ∫_L E · dl ∫_Σ rotE · n dΣ N.B. con Σ superficie aperta

rot E = Λ×E = u_x u_y u_z

∂/∂x ∂/∂y ∂/∂z

E_x E_y E_z

poiché E è conservativo: ∫_Σ rotE · n dΣ = 0 poiché rotE = 0

Dipolo elettrico momento di dipolo P = q d u_s +q -q u_s: -

r = distanza di un punto da O posto in d/2, r >> d

allora E_p = -ΛV_p

potenziale di dipolo: V_p = V_+q + V_-q = q/4πε_o (1/r⁺ - 1/r^-) = q/4πε_o (r^- - r⁺ / r^-r⁺)

r^- - r⁺ = d cosθ con θ = angolo asse d e r, r^-r⁺ = r²

V_p = q/4πε_o dcosθ/r² = 1/4πε_o p·r/r³

calcolo E_p = -ΛV_p: E_p = -1/4πε_o Λ(p·r/r³) = -1/4πε_o [1/r³(Λp·r) + p·r(Λ1/r³)]

r = (xu_x + yu_y + zu_z)

p = (p_xu_x + p_yu_y + p_zu_z)  

r³ = (x² + y² + z²)^3/2

Λp·r = Λ(p_xx + p_yy + p_zz) = ∂p_xx/∂x + ∂p_yy/∂y + ∂p_zz/∂z = p_xu_x + p_yu_y + p_zu_z = p

Λ1/r³ = Λ 1/(x² + y² + z²)^3/2

= ∂1/(x² + y² + z²)^3/2/∂x + ∂1/(x² + y² + z²)^3/2/∂y + ∂1/(x² + y² + z²)^3/2/∂z

= -3/2 1/(x² + y² + z²)^5/2 2x u_x + -3/2 1/(x² + y² + z²)^5/2 2y u_y + -3/2 1/(x² + y² + z²)^5/2 2z u_z

= -3/r⁵ (xu_x + yu_y + zu_z) = -3r/r⁵

E_p = -1/4πε_o [p/r³ - 3(p·r) r / r⁵] = 1/4πε_o [(p·r)·r / r⁵ - p/r³]

E_p = componente r - componente p

Dielettrico: caratterizzato da ε_r = costante dielettrica relativa = C_diel/C_vuoto >1 C_diel > C_vuoto

I dipoli molecolari/atomici si orientano secondo E, annullando gli effetti del loro campo all'interno del dielettrico, ma generando all'esterno una carica superficiale ∂q e densità ∂p, che genera un campo E_diel opposto e proporzionale a E: E_tot = E - E_diel

vettore polarizzazione: P = Σp_i / volume ∂p = (P · n)

(ci sono condizioni per cui ho densità di cariche nel volume del dielettrico _p ~ dwP = ΛP)

P = ε_oχE χ = suscettività elettrica

Legge di Gauss: dwE = ΛE = /ε_o = ( _{libera p}) / ε_o    

dwE = ( _libera - ΛP) / ε_o Λ[ε_o E + P] = _libera

[ε_o E + P] = D = spostamento elettrico dwD = ρ_libera

D = ε_o E + P = ε_o E + ε_o χ E = ε_o E (1+χ) = ε_o E ε_r

E_tot = E_o ε_r

Dielettrico nel condensatore: date 2 maglie a distanza d e un dielettrico spesso h:

C = C_od / d-h

Polarizzabilità atomica p = q d = α E α = polarizzabilità atomica

4πd²E = /ε_o · 4πr³/3 E = d / 3 ε_o = q d / 4πr³ε_o = p/4πr³ε_o α_d = 4πR³ε_o R= r atomo

p = α_oE α_orientamento ≠ α_deformazione ( = 4πR³ε_o )

L'energia cinetica (temperatura) dispone casualmente i dipoli, E li fa orientare: p ~ 1/T

in genere: α_o = p_o²/3kT α = α_o + α_d α_o dipende dal materiale.

Liquidi: α = (3ε_o/N) (ε_r - 1)/(ε_r + 2) N = num dipoli / volume

Gas: ε_r ~ 1 α = (ε_o/N) (ε_r - 1)

dimostrazione 2^a legge di Ohm: V = RI V = E l_filo R = A/l I = J A

E = J J = σ E σ = 1/ρ = conducibilità

In genere quindi J // E // p. Alcuni materiali p non è // E, quindi

p = ε_o χ E χ (χ_x, χ_y, χ_z) costanti dette tensori

Drude: considero una corrente in un metallo: F = q_(e-) E a = q/m E

gli elettroni urtano con i cationi: tempo medio tra due urti: т

v_deriva = a т = q/m E т J = n q v_d v_d = J/nq

J = nq²тE /m quindi σ = 1/ρ = conducibilità = nq²т /m

т = m σ / n q² conosco v_termica т = l (distanza tra due urti) ½mv_th² = 3/2 k T

la distanza tra ioni è d ~ 5 Ǻ nd = l

Nel metallo gli elettroni, se raggiungono velocità suff. elevate, si comportano come onde, e se il materiale è un cristallo perfetto, si muovono senza interagire quindi la resistenza è nulla.

ELETTROMAGNETISMO

Forza di Lorentz: F = q v×B u-m.: Tesla = Kg / A s²

La forza di Lorentz non compie lavoro, poiché è una forza sempre centripeta: a = v²/R

v_B:

moto circolare uniforme: qvB = mv²/ρ

raggio di curvatura: ρ = mv/qB

v e B con angolo

moto elicoidale, devo scomporre v in componenti parallelo a B, che rimane inalterato, e perpendicolare a B, che subisce l'effetto della F di Lorentz.

v // B

B non varia la velocità.

Effetto Hall: Data una piastra di spessore a, lunghezza b, e una corrente i che la percorre, immersa in un campo magnetico B perpendicolare ad essa: i = J a b = N q v_d

Il campo magnetico B curva le velocità con F_m = - q v_d B e sposta gli elettroni da un lato della lastra, generando una carica negativa da un lato e una positiva dall'altro, creando così un campo elettrico il cui V è misurabile. V = E b

E applica sulle cariche una forza F_e opposta a F_m, in condizioni di equilibrio abbiamo:   q E = q v_d B

E = v_d B ΔV / b = v_d B B = ΔV / b v_d ( v_d = i / N q a b ) B = ΔV N q / a i

Campo generato da un circuito: dato un circuito chiuso , dato l'elementino di circuito dl, R il

vettore che indica il punto P e R' quello che indica dl, B calcolato in P vale:

B_(p) = μ_o i / 2π ∫_γ [dl × (R-R') / (R-R')³] (Formula di Laplace)

μ_o = 4π 10^-7 Henry/m = N C^-2 m^-1 cost. di permeabilità magnetica nel vuoto

Filo percorso da corrente F = i l×B F è centripeta e B è tangente a una circonferenza col centro nel filo.

Se ci sono due fili, entrambi generano un campo e si attrarranno se i hanno lo stesso verso oppure si respingeranno, con F: F = (μ_o/2π)(I₁I₂)(l/d)

Formula di Biot-Savar: Dato un filo l u_z passante per O, considero l'elementino dl e un punto P posto a distanza d, allora: O-dl = R' = z O-P = d = R u_x dl-P = R-R'= P-dl

detto θ l'angolo tra asse z e R-R', allora B:

B = i μ_o / 4π ∫dz senθ / (r-r')² sostituisco: (R-R')senθ = d z/d = cotgθ

B = μ_o/4π i/d ∫₀^π -senθ dθ B = μ_o/2π i/d

Campo generato da una spira consideriamo asse z passante per O centro della spira di raggio a e P posto su z di coordinata R, θ l'angolo tra l'asse z e R-R' congiungente l'elementino di spira dl = R' a P. Allora avremmo che:

B = i μ_o / 4π ∫dl senθ / (R-R')² sostituisco: R-R' = √(a² + z²) senθ = a / √(a²+ z²)

B = (i μ_o / 4π) (a / (a²+z²)^3/2) ∫_spira dl = (i μ_o / 4π) (a / (a²+z²)^3/2) 2πa    B = (i μ_o / 2) (a² / (a²+z²)^3/2)

Se z>>a allora B = (i μ_o / 2) (a² / z³)

Dipolo magnetico m = i · A_{rea circuito} · n_ormale (n determinata da regola mano destra)

B_spira = μ_o/2π m/z³

Campo generato da un solenoide: dato un solenoide approssimato a un numero N di spire di lunghezza l, considero il campo lungo il suo asse centrale z:

η = N/l = densità di spire. considero tratto infinitesimo: dz dN = η dz

dB = campo di una spira · dN: dB = (i μ_o / 2) (a² / (a²+z²)^3/2) ηdz

Dato θ angolo tra asse z e dl, sostituisco: z = a cotgθ dz = a dθ / senθ a/√(a² + z²) = senθ

B = (i μ_o η / 2) ∫ senθ dθ = (i μ_o η / 2) |cosθ|_θ1^θ2

se il solenoide è infinito θ₁ = 0, θ₂ = 180° B = i μ_o η

Filo immerso in un campo magnetico esterno:

F = (q v×B)(num e^- = N S l) N = densità di corrente, S = sezione filo

sostituisco J = Nqv F = J×B S l  sostituisco J S = i F = i l×B

Spira immersa in un campo magnetico esterno:

considero una spira quadrata di lato l e B che forma con la normale n alla superficie un angolo θ, considero i lati uno alla volta:

l₁: F₁ = l₁×B i cosθ l₃: F₃ = l₃×B i cosθ

poiché l₁ = -l₃ F₁ + F₃ = 0 perché entrambe hanno la stessa retta d'azione posta sul piano della spira e perpendicolare nel centro di l a l.

F₂ e F₄ sono una coppia di forze = i l_2,4×B

Momento torcente: M_o = i l₂ l₄ B senθ = m B senθ

Legge di Gauss Φ_B = ∫_Σ B n dΣ = 0

Φ_B = ∫_v dwB dv = ∫_v ΛB dv dwB = 0 non esistono le sorgenti del campo B

Circuitazione: Γ_B = ∫_γ B dl = μ_o I_concatenata Legge di Ampère (non sempre valida)

Γ_B = ∫_Σ rotB n dΣ = ∫_Σ (Λ×B) n dΣ con Σ superficie aperta sottesa da l linea chiusa

Γ_B = ∫_Σ μ_o J n dΣ rot B = μ_o J

Limitazioni legge di Ampère: Data la relazione Λ(Λ×B) = Λ(μ_o J), il primo termine è 0, allora: ΛJ = 0 che è valida sempre se J è solenoidale, ovvero quando:

Φ_J = _v ΛJ dv = J n dΣ = 0 Il flusso è uguale a 0 se la densità di corrente è stazionaria, ovvero non si accumulano cariche: I_netto = -∂q/∂t = 0 ΛJ = -∂q/∂t se ≠ 0 Ampère non valida

Formula di Biot-Savar: B dl = μ_o I_conc scelgo l = circonf. centro nel filo tg a B = 2πr

B = μ_o/2π I/r

Corrente cilindrica: ext: B = μ_o/2π I/r

int: B = μ_o J r / 2

Teorema di Helmotz: Detto F campo vettoriale, U il potenziale e W l'energia, allora:

U = 1/4π _R3 (rotF ∙ F') / |F-F'| dv'

W = 1/4π _R3 (rotF ∙ r') / |r-r'| dv'

Energia di un campo magnetico dU_B = B²/2μ_o dV

Costanza del valore di B all'interno del solenoide: ∫_γ B dl = μ_o I_conc , se stabilisco un percorso rettangolare interno al solenoide, con 2 lati // a B, di cui uno coincidente con l'asse centrale, l'integrale è uguale a: = ∫ B dl_par1 + ∫ B dl_par2 + ∫ B dl₁ + ∫ B dl₂ = μ_o I_conc = 0, i componenti perpendicolari dl1 e dl2 sono uguali a 0, quindi, ∫ B dl_par1 + ∫ B dl_par2 = 0, B al centro è uguale a B non al centro!

Annullamento del campo all'esterno del solenoide stesso discorso di prima ma con un lato // esterno, per cui ∫ B dl_int + ∫ B dl_ext = μ_o I_{conc =} μ_o I η l,

il primo termine da esattamente μ_o I η l, allora il secondo non può che essere uguale a zero.

Energia del campo di un solenoide U = 1/2μ_o B² A_spira l = ½ μ_o η² A l I²

autoinduttanza = L = μ_o η² A l è legata a geometria del solenoide U = L I²

Autoinduttanza: calcolo Φ_B sulla superficie aperta Σ racchiusa dal circuito,

che è quindi ≠ 0 = B n dΣ,

L = Φ_{B autoconcatenato} / I _circuito (u.m. Henry = T m² / A)

Autooinduttanza di un solenoide: Φ_{B autoconcatenato} = μ_o I η A_spira N_spire ( = ηl) = μ_o η² A l I

L = μ_o η² A l I / I = μ_o η² A l   quindi: Φ_B = L I, U_B = ½ L I²

Forza fra due circuiti: F_{2 su 1} = I₁ dl₁ × B₂

se i circuiti sono 2 fili paralleli: F₂/l₂ = (μ_o / 2π) (I₁I₂ / d) (forza su unità di lunghezza)

Magnetismo nella materia

Affianco al termine μ_o, nella formula di Laplace, il termine μ_r = B/B_o (<1 diamagnetismo, >1 paramagnetismo, >>1 ferromagnetismo dipende cmq dal campo generante, ovvero da I nel circuito).

Diamagnetismo

considero l'orbita dell'elettrone nell'atomo come una spira di raggio r_o, e il campo B che ne attraversa l'area con un certo angolo.

1. I = e^-/t = e^- v_o/2πr_o   v_o = velocità elettrone senza B_ext
2. F_lorentz = -e^- v×B_ext  v = velocità centripeta elettrone a effetto compiuto, B non deforma l'orbita
3. Forze agenti = F_coloumb agisce B F_coloumb + F_lorentz   F = 1/4πε_o e²/r_o + evB = m v_o²/r_o (v≠v_o)
4. evB = m/r_o (v + v_o) (v - v_o)  dati: v+v_o ~ 2v_o e v-v_o = Δv ~ eBr_o/2m = Δv_(B) che provoca ΔI
5. ΔI = eΔv / 2πr_o = e eBr_o / 2πr_o 2m = e²B/4πm
6. mom = momento di dipolo magnetico = ΔI π r_o² = e²B/4πm πr_o² = e²Br_o² / 4m
7. mom_tot = -∑ e²Br_o² / 4m (mom ÷ B ma verso opposto)

quindi B genera momenti magnetici che generano minicampi opposti a B, che perciò lo indeboliscono. In genere i materiali diamagnetici hanno orbitali con gli spin entrambi occupati, e quindi non presentano momenti magnetici propri. Il diamagnetismo non dipende dalla temperatura.

Paramagnetismo

in materiali con elettroni spaiati, presenza quindi di un momento magnetico di spin. In presenza di un campo esterno la spira ruota finchè mom_o non è orientato come B (somma massima). Tuttavia si presenta anche il fenomeno del diamagnetismo, con la formazione di un mom_diam opposto a B.

Avrò quindi: B_ext e mom_o , e B_int generato da mom_diam , in totale B > B_o .

B_ext genera mom_diam che indebolisce B, ma orienta mom_o in modo da ottenere somma massima.

Il fenomeno del paramagnetismo diminuisce all'aumentare di Temperatura, gli atomi vibrano, si ha meno orientazione degli orbitali.

Magnetizzazione

∫ B dl = μ_o (I_conc + I_{magnetizzazione atomo}) Λ×B = μ_o (j_conc + j_magn)

devo trovare legame M = magnetizzazione = (∑mom_i) / Volume

considero 2 volumetti di lato dx, dy, dz affiancati sulla faccia dx dz, ognuno contenente I antiorario, sullo spigolo dz avrò a sinistra una I che sale, e a destra una I che scende, ognuna producente il suo M lungo x M_x che varia di volumetto in volumetto:

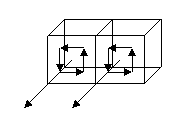dy

dx I₁ I₂ M'_x = M_x + δM_x/δy ∙ dy

I₁A₁ = I₁ dy dz = M_x dx dy dz I₁ = M_x dx

dz I₂ dy dz =(M_x + δM_x/δy ∙ dy) dx dy dz I₂ = (M_x + δM_x/δy ∙ dy) dx

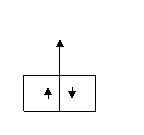
M_x M'_x I'_z = I₁ - I₂ = - δM_x/δy ∙ dx dy

z I' = I₁-I₂ I₃

nelle altre dimensioni:

I₁ I₂ M'_y = M_y + M_y/ x ∙ dx I₁

I₃ = M_y dz + M_y/ x ∙ dx dz

I'₃ - I' = I''_z = M_y/ x ∙ dx dz

J_{z magn} M_y/ x - Mx y) = (Λ×M)_z

quindi Λ×B = μ_oj + μ_o Λ×M Λ×B/μ_o = j + Λ×M detti: H = B/μ_o - M e Λ×H = j

allora ∫H dl = I

se ( _{o o r} e (∫B dl = (I_conc + I_magn) μ_o) ×B/ _o = j + j_magn e j_magn = Λ×M

ottengo: H = B/ _o - M Λ×H = j ∫H dl = I

Conservazione componenti di B:

considero il passaggio da un materiale 1 con μ_r1 e materiale 2 con μ_r2 e un percorso rettangolare che li comprenda entrambi, e per cui dl di passaggio da 1 a 2 << dl nei materiali.

∫_γH dl = I_conc = 0 H_tg1 dl - H_tg2 dl = 0 H_tg1 = H_tg2

se invece considero un cilindro infinitesimo, in cui dh << ds, allora:

∫_ΣB n dΣ = 0 B_{norm 2} ds - B_{norm 1} ds = 0 B_{norm 1} = B_{norm 2}