CAMPO MAGNETICO. FORZA MAGNETICA - INTERAZIONE MAGETICA. CAMPO MAGNETICO

Esistono solo due specie di poli: positivi e negativi. Inoltre i poli di un stesso magnete sono sempre di segno opposto. Se un magnete lo dividiamo in due parti, avremo 2 magneti che hanno entrambi polo positivo e polo negativo.

2. Se si avvicina ad un pezzo di magnetite una bacchetta sottile di ferro, questo acquista la proprietà di attirare la limatura di ferro. Si dice che essa è magnetizzata e viene detta magnete artificiale o calamita, e presenta due poli magnetici di segno opposto. Se è di piccole dimensioni la bacchetta viene detta ago magnetico.
3. Se l'ago magnetico viene sospeso ad un filo, esso tende a disporsi parallelamente al meridiano terrestre. L'esperienza mostra l'esistenza di un campo magnetico naturale, il campo magnetico terrestre e mette in evidenza un comportamento dell'ago magnetico del tutto analogo a quello di un dipolo elettrico posto in un campo elettrico E.

L'ago magnetico si comporta come un dipolo magnetico che lasciato libero si orienta nella direzione e verso del campo magnetico esistente nel punto dove è posto.

Il polo che si orienta verso Nord è detto Polo nord ed è positivo; viceversa il polo sud è negativo.

4. Sebbene la forza che si esercita tra i due poli magnetici sia simile a quella che si esercita tra due cariche elettriche, esiste tra di esse una differenza fondamentale. Una carica elettrica, positiva o negativa, può sempre essere isolata. Invece il monopolo magnetico non esiste. L'induzione classica è costituita dall'esperimento della calamita spezzata.
5. Sono significative anche le esperienze condotte con limatura di ferro posta in vicinanza di un magnete. I granelli si dispongono in modo ordinato lungo le linee regolari, ovvero le linee di campo magnetico B.

Questo fenomeno veniva studiato con la magnetostatica. E' stato poi scoperto che non sono solo i magneti naturali a comportarsi in questo modo, ma anche i materiali ferromagnetici, se sono posti ad un ciclo di isteresi, si comportano nello stesso modo (magneti artificiali).

Anche un circuito sottoposto a corrente, presenta questo fenomeno.

Abbiamo quindi:

1. Magneti naturali;
2. Magneti artificiali;
3. Circuiti elettrici.

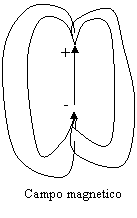
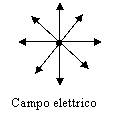
Nel campo elettrico, abbiamo visto che possiamo usare per la misura del campo, una carica di prova q, talmente piccola in modo che non influenzi il campo.

Nel campo magnetico, la carica di prova non sarà mai osservabile su una singola carica, ma su un dipolo magnetico (questa sarà la nostra carica di prova). Esistono oggetti che si comportano come dipoli magnetici (aghi magnetici della bussola). Questi sono molto piccoli e non influenzano il campo magnetico, ma si mettono in direzione del campo.

Questa osservazione è importante, in quanto ci dice la I equazione di Maxwell per il campo magnetico.

∫ B d I equazione di Maxwell per il campo magnetico

Il flusso sarà 0 perché il numero di linee uscenti, sarà uguale al numero di dipoli entranti (in quanto siamo di fronte ad un dipolo magnetico).

ELETTRICITA' E MAGNETISMO

Gli elementi costitutivi dei magneti sono i dipoli magnetici, che possono essere caratterizzati da un momento magnetico m.

Siccome la non isolabilità dei poli magnetici è confermata, siamo portati a supporre che atomi e molecole, come possiedono una struttura elettrica, abbiano anche un momento di dipolo magnetico.

Oersted mostrò che un ago magnetico, posto in prossimità di un filo percorso da corrente, tende ad assumere una ben definita posizione di equilibrio. Ponendo in un piano perpendicolare un filo percorso da corrente della limatura di ferro, i granelli si addensano lungo circonferenze con centro il filo.

Quindi il filo percorso da corrente produce un campo magnetico B e l'ago e la limatura di ferro si orientano parallelamente al campo magnetico esistente nel punto in cui sono posti. In seguito Ampere dimostro che anche due fili percorsi da corrente interagiscono e intuì che le azioni magnetiche non sono altro che la manifestazione dell'interazione tra cariche elettriche in movimento, ponendo le basi della teoria attuale del magnetismo.

Per spiegare le azioni sui magneti bisogna pensare che in ogni atomo o in ogni molecola devono esistere delle correnti microscopiche locali, che prendono il nome di correnti molecolari di Ampere o correnti Amperiane;

L'interazione tra un circuito percorso da corrente ed un magnete è il risultato delle interazioni tra gli elettroni liberi in moto nel conduttore e le microcorrenti presenti nel materiale magnetizzato. Infine l'interazione tra due magneti è il risultato delle interazioni delle correnti microscopiche in essi presenti. Tutto ciò presuppone che il moto degli elettroni negli atomi e nelle molecole, dia origine a momenti magnetici atomici elementari.

Maxwell dimostrò che nel caso più generale un campo elettrico e un campo magnetico non possono avere esistenza indipendente e vanno unificati nell'unico concetto di campo elettromagnetico.

Campo elettrico e campo magnetico hanno significato relativo: un interazione magnetica in un sistema di riferimento inerziale può apparire elettrica in un altro sistema di riferimento inerziale e viceversa.

FORZA MAGNETICA SU UNA CARICA IN MOTO

Le azioni magnetiche sono il risultato dell'interazione tra cariche in moto:

adottando la rappresentazione tramite un campo, diciamo che l'azione magnetica è dovuta al fatto che un sistema di cariche in moto genera un campo magnetico, che indichiamo con il simbolo B e che l'altro sistema di cariche in moto risente di una forza in quanto immerso in B.

Consideriamo una particella, di massa m e carica q, posta in un campo magnetico B. Se la particella è ferma in un sistema di riferimento solidale alle sorgenti del campo si trova che su essa non agisce nessuna forza, poiché l'interazione magnetica si manifesta solo tra cariche in movimento. Se invece la particella è in moto con velocità V rispetto al sistema di riferimento dato, su di essa agisce la forza di Lorentz.

F= qV x B FORZA DI LORENTZ

Il cui modulo è F= qvB senθ. Si misura in Tesla= Kg

As²

dove θ è l'angolo formato da V e B. Quindi la forza è nulla se la velocità è parallela al campo B e massima se V   B.

La direzione della forza è ortogonale al piano individuato dai vettori V e B, e il verso è determinato dalla nota regola del prodotto vettoriale se la carica è positiva, ed è opposto se la carica è negativa. Per il verso si fa riferimento alla regola della vite.

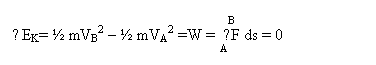
In particolare la forza è sempre ortogonale alla velocità, cioè alla traiettoria e pertanto, in base alla definizione di lavoro e di energia cinetica, si ha:

Quindi per un qualsiasi spostamento da A a B nella regione in cui esiste il campo magnetico B l'energia cinetica della particella resta costante, in quanto la forza di Lorentz non compie lavoro sulla particella.

Quando una particella carica si muove in campo magnetico, la sua velocità cambia direzione, ma non modulo.

FORZA MAGNETICA SU UN CONDUTTORE PERCORSO DA CORRENTE

La corrente elettrica di un conduttore è dovuta al moto degli elettroni, sotto l'azione del campo elettrico applicato tramite un generatore i, se n è il numero di elettroni liberi per unità di volume, ciascuno con carica -e, e Vd la loro velocità di deriva, la densità di corrente si scrive:

j= -neVd

ed è parallela e concorde al campo elettrico applicato.

Quando il conduttore percorso da corrente è immerso in un campo magnetico a ciascun elettrone è applicata la forza di Lorentz:

F_L = -eVd x B

In un tratto di conduttore lungo ds e di sezione sono contenuti n ds elettroni e la forza risultante è:

dF = n dsF_L = -( ds) neVd x B = ds j x B

Considerando un conduttore filiforme, e ricordando che j è la corrente i che percorre il filo, orientiamo ds come j e otteniamo:

dF= i ds x B SECONDA LEGGE ELEMENTARE DI LAPLACE

serve per calcolare la forza che un campo magnetico esercita su una corrente.

La forza magnetica su un tratto infinitesimo di filo percorso da corrente, è ortogonale al filo e al campo magnetico, ed è orientata rispetto a ds e B secondo la regola della vite.

|dF|= i B ds senθ

OSS: Le caratteristiche della forza non dipendono dal segno dei portatori di carica ed essa è sempre proporzionale all'intensità di corrente.

Per ottenere la forza su un tratto di filo di estremi A e B:

_B

F= i ∫ ds x B

^A

(i si porta fuori dal segno di integrale perché è costante su ciascuna sezione del filo).

Nel caso particolar in cui B è uniforme e il conduttore è rettilineo di lunghezza l:

_B

F= i ( ds) x B

^A

poiché il modulo del campo e θ formato con ds sono costanti.

MOTO DI UNA PARTICELLA CARICA IN CAMPO MAGNETICO B

Supponiamo che B sia uniforme in una certa regione e che la velocità iniziale della particella sia ortogonale a B.

La forza di Lorentz è anch'essa ortogonale a B e produce una variazione della direzione della velocità ancora ortogonale a B e quindi la velocità in qualsiasi istante successivo sta nel piano ortogonale a B individuato dalla velocità iniziale.

Il moto della particella si svolge in tale piano e la legge del moto è:

F= qvB = ma_n = m v²

r

da cui otteniamo il raggio di curvatura della traiettoria

r = mv = p (p= modulo della quantità di moto)

qB qB

La velocità non cambia in modulo perché la forza è esclusivamente centripeta.

Inoltre siccome il raggio è costante, la traiettoria è un arco di circonferenza di raggio r o una circonferenza completa se la particella resta sempre nella regione in cui è definito B.

Il moto lungo la traiettoria, è circolare uniforme con velocità uguale a quella iniziale e velocità angolare:

ω = v = qB

r m

Per quanto riguarda il periodo:

T= 2Π = 2Πm

ω qB

da cui la frequenza è:

ν= 1 = ω = qB

T 2Π 2Πm

MOTO DI UNA CARICA IN UN CAMPO MAGNETICO

Supponiamo che B sia uniforme.

B e V formano un angolo qualsiasi.

La forza sulla carica può essere espressa come:

F = ma= qv x B = m dv

dt

Ma V rispetto a B si può scomporre secondo la regola del parallel.

V = V_par + V

da cui F = qV_par x B + qV x B = F_par + F

F_par = 0 da cui a=0 e V_par=cost per cui il moto è uniforme

F ≠ 0 da cui F B segue che F = F , a ≠0, V ≠ cost per cui il moto non è uniforme

Vediamo la natura del moto in direzione perpendicolare al campo B.

_B

F non compie lavoro, per cui ω = F dl = 0 da cui

^A

ω = ∆u_k = 0, segue che u_k = ½ mv² = costante, poiché v è costante, e varia solo in direzione.

Abbiamo che F = qV B segue che a= q V B = costante

m

Siccome a v si tratta di un moto circolare uniforme.

F = ma_c = v² m = qV B segue che R = mv

R qB R è il raggio del moto circolare uniforme che avviene nel piano ortogonale a B

Riassumendo:

V_par = costante

V    = costante, ma V ≠ costante MOTO ELICOIDALE A PASSO COSTANTE

Elica percorsa in senso orario o antiorario, a seconda

che q>0 o q<0.

Se la componente parallela a B della velocità è nulla, il moto è circolare uniforme ed è detto moto ciclotrone con frequenza:

	FORMULE DI LAPLACE dB = μ0 ids μt x μr (campo magnetico 4Π r2 prodotto da corrente dF = i ds x B (Forza magnetica su corrente

2Πv = ω = V = qB

R m

T= 2Π = 1

ω ν