|
|
| |
Sia Y una variabile statistica ottenuta a partire dalla variabile X, attraverso la trasformazione:
Y=g(X)
Applicando il teorema della media, possiamo calcolare la media e la varianza della variabile Y senza per questo dover valutare la sua distribuzione di frequenza, infatti
![]()
![]()
il che implica comunque di dover calcolare le sommatorie rispetto alla distribuzione della X.
Supponiamo ora che la trasformazione g sia lineare
![]()
per le proprieta' di linearita' dell'operatore media, possiamo ricavare direttamente (senza fare alcuna sommatoria) la media di Y a partire dalla media di X, infatti
![]()
In maniera del tutto analoga e' possibile ricavare direttamente la varianza di Y a partire dalla varianza di X, infatti:
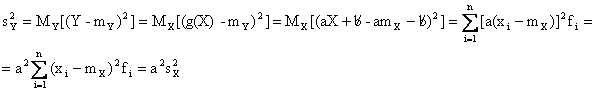
Le formule ricavate sono dette di propagazione della media e della varianza.
Nel caso in cui la trasformazione g non sia lineare, e' possibile linearizzarla intorno al valore della media di X, applicare il teorema della media alla trasformazione linearizzata e ottenere delle formule di propagazione approssimate.
Il livello di approssimazione di tali formule dipendera' da quello con cui la trasformazione linearizzata approssima quella non lineare. L'errore sara' contenuto se:
la trasformazione nell'intorno della media e' sufficientemente regolare
la frequenza della variabile X e' concentrata in tale intorno.
La regolarita' implica che la retta tangente si discosti poco dalla curva g(x,y) nell'intorno della media, intorno nel quale l'errore commesso nel sostituire alla g la tangente e' moltiplicato pre frequenze elevate; al di fuori di tale intorno l'errore maggiore viene moltiplicato per frequenze trascurabili
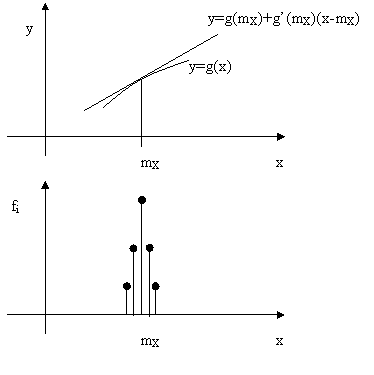
Posto dunque, in maniera approssimata
![]()
Si ricava
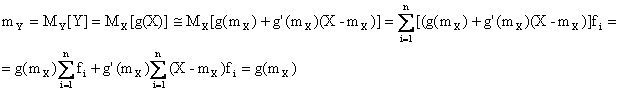
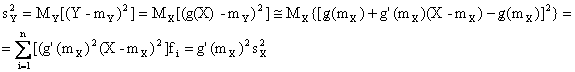
|
Formule di propagazione della media e della varianza |
|
|
Caso lineare |
Caso non lineare |
|
Y=aX+b |
Y=g(X) |
|
|
|
|
|
|
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026