studiare le caratteristiche di un circuito RL mediante

Oscilloscopio dual-trace 30Hz Elettronica Veneta modello 0 30-82/EV

Induttore

RELAZIONE: la prova sperimentale consiste nello studiare un circuit 444j94e o ohmico-induttivo. Prima di poter effettuare questa prova bisogna però precisare alcuni punti fondamentali.

Se una corrente alternata percorre, ad esempio, una bobina, avremo che questa offre, al passaggio della corrente, oltre alla sua resistenza ohmica, anche un'altra resistenza dovuta all'induttanza induttiva XL. Schematicamente risulta conveniente rappresentare separatamente la R e la L come indicato nella figura seguente.

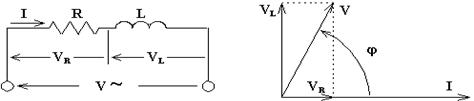
Ovviamente, applicando ad un circuito così costituito una certa tensione, la corrente provoca una caduta di tensione Vr, attraversando la resistenza ed una caduta di tensione VL, attraverso l'induttanza. La caduta totale di tensione non può essere ricavata dalla somma aritmetica di VR e VL ma dalla loro somma vettoriale. La rappresentazione grafica, quindi, viene mostrata dallo schema descritto nella figura qui sopra, in cui VL si trova sfasata di 90° in anticipo rispetto alla corrente I a causa dell'induttanza, mentre VR trovasi in fase con I per il circuito ohmico. Componendo i due vettori relativi a VR e VL, il teorema di Pitagora, si avrà la caduta totale di tensione V. L'espressione rappresenta l'ostacolo complessivo che la corrente alternata incontra nel circuito per la presenza della resistenza e della reattanza; questa grandezza viene detta impedenza induttiva del circuito e si indica con la lettera Z.

Per cui si ha V=I·Z da questa formula si ricava:

I=V/Z e Z=V/I

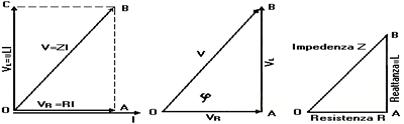
La resistenza, la reattanza induttiva e l'impedenza vengono misurate in ohm; in effetti l'impedenza non è altro che una resistenza apparente, il cui valore è senz'altro maggiore della resistenza ohmica e, graficamente, è rappresentata dall'ipotenusa del triangolo rettangolo OAB, avente i cateti uguali rispettivamente ad R ed L. Tale triangolo viene detto triangolo dell'impedenza ed è ricavato da quello delle cadute di tensione, dividendo i vettori proporzionali per la corrente I. Il rapporto tra la resistenza R del circuito e la sua impedenza Z indica il coseno trigonometrico dell'angolo  che rappresenta l'angolo j di sfasamento tra i vettori di tensione e corrente.

Per effettuare la prova ci serviamo oltre che alla resistenza e all'induttore di un oscilloscopio e di due tra i più comuni strumenti di misura, un voltmetro e un amperometro. L'amperometro e il voltmetro serviranno a far si che si possano fissare i valori della corrente e di tensione da noi stabiliti. L'oscilloscopio, mostrato nella figura qui seguente, è uno strumento utilizzato per la misurazione di intensità di corrente, di differenza di potenziale e misurazioni di frequenza, il suo principale vantaggio rispetto ad altri strumenti, però è che permette di visualizzare la variazione nel tempo dei segnali applicati alle sue entrate, di conseguenza verrà utilizzato per lo studio delle sinusoidi della corrente e della tensione.

Dopo aver assemblato il circuito si potrà dare inizio alla prova che sarà composta nel seguente modo:

in corrente continua fissare il valore di tensione opportuno (V=21.2V) per far si che circoli una corrente pari a 2A. Questa prima fase della prova viene effettuata senza l'impiego dell'unità di ferro all'interno dell'induttore;

I

V

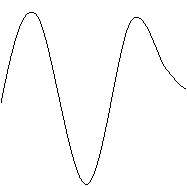
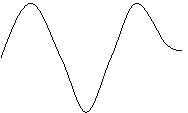
in corrente alternata ad una frequenza di 50Hz fissare il valore di tensione opportuno (V=56.6V) per far si che circoli la stessa corrente, pari a 2A, della fase precedente. Come si può notare dal grafico seguente, sia la corrente che la tensione sono grandezze isofrequenziali (Periodo=20ms). Anche questa seconda fase viene effettuata senza l'impiego dell'unità di ferro all'intero dell'induttore;

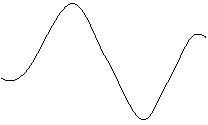
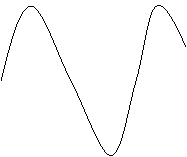
in corrente alternata ad una frequenza di 50Hz fissare lo stesso valore di tensione della fase precedente, 56.6V, e controllare quanta corrente circola (I=0.21A) a parità di tensione. Come si può notare dal grafico seguente la corrente è in ritardo di un certo angolo X rispetto alla tensione. Questo angolo risulterà, dopo alcuni brevi calcoli, essere di 64.8°. Questa terza fase della prova viene effettuata introducendo l'unità di ferro all'interno dell'induttore;

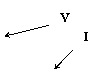
in corrente alternata ad una frequenza di 50Hz fissare un valore opportuno di tensione (V=430V) per far si che circoli una corrente pari a 2A. Anche questa quarta ed ultima fase della prova viene effettuata introducendo l'unità di ferro all'interno dell'induttore.

CALCOLI:

Corrente Continua

V=21.2V

I=2A

R=V/I=21.2/2=10.6W Resistenza del circuito

Corrente alternata 50Hz (induttore senza l'unità di ferro)

V=56.6V

I=2A

T=20ms

Z=V/I=56.6/2=28.3W Impedenza del circuito

XL wL=  Z² - R² = 28.3² - 10.6² = 26.24W Reattanza induttiva

j=arcTg(XL/R)=arcTg(26.24/10.6)=arcTg2.475=67.9°    Angolo di sfasamento

Corrente Alternata 50Hz (induttore con l'unità di ferro)

V=56.6V

I=0.21A

Z=V/I=56.6/0.21=269.52W Impedenza del circuito

XL wL=  Z² - R² = W Reattanza induttiva

j=arcTg(XL/R)=arcTg(269.31/10.6)=arcTg25.41=87.7°  Angolo di sfasamento

Corrente Alternata 50Hz (induttore con l'unità di ferro)

V=430V

I=2A

Z=V/I=430/2=215W

XL wL=  Z² - R² = 215² - 10.6² = 214.74W Reattanza induttiva

j=arcTg(XL/R)=arcTg(214.74/10.6)=arcTg20.26=87.17° Angolo di sfasamento

TABELLA:

CONCLUSIONI: si può quindi dire che in un circuito ohmico-induttivo, sia I il vettore rappresentativo della corrente che attraversa il circuito, la caduta ohmica dovuta alla resistenza R è rappresentata dal vettore VR di ampiezza

VR=R·I

in fase con il vettore I. L'induttanza L oppone alla corrente, infatti, una reattanza XL pfL, la quale determina una caduta induttiva che è rappresentata da un vettore VL di ampiezza

VL=XL·I

e sfasato di 90° in anticipo rispetto al vettore I.

Ne segue allora che per mantenere nel circuito la corrente I si dovrà applicare al circuito stesso una tensione definita in ampiezza e fase dal vettore risultante

V=VR+VL