|
|
| |
Un circuito elettronico in grado di generare un segnale sinusoidale di frequenza predeterminata, senza l'intervento di alcuna eccitazione esterna che non sia la consueta alimentazione in continua, prende il nome di oscillatore sinusoidale.
Il modo classico di generare un segnale sinusoidale consiste nel portare un amplificatore, sottoposto a reazione positiva, in oscillazione spontanea. Glio oscillatori trovano impiego in vari campi sia in bassa frequenza (testing di apparecchi audio, pilotaggio di trasduttori) che in alta frequenza (generazione di portanti radio TV, conversioni di frequenza ecc).
In fig. è rappresentato lo schema generale di un amplificatore rea 656b16g zionato (positivamente).
Mantenendo aperto S2 e
chiudendo S1, si applichi il segnale sinusoidale xs
all'ingresso del blocco G (che nella pratica è un amplificatore); otteniamo
che: xi=xs e xf=GHxi
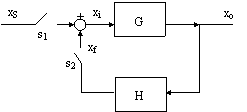
Mantenendo aperto S2 e chiudendo S1, si applichi il segnale sinusoidale xs all'ingresso del blocco G (che nella pratica è un amplificatore); otteniamo che:
xi=xs e xf=GHxi
Nell'ipotesi che esista un'unica frequenza Fo per la quale la fase di GH sia uguale a 0, ovvero che xf e xi siano in fase, possono aversi i seguenti tre casi:
|GH|=1, risulta allora |xf|=|xs|; chiudendo S2 e aprendo simultaneamente S1 l'amplificatore si autoeccita, mantenendo in uscita l'oscillazione a frequenza Fo, di ampiezza costante.
|GH|<1, risulta allora |xf|<|xs|; chiudendo S2 e aprendo simultaneamente S1 l'oscillazione a frequenza Fo si smorza gradualmente fino ad esaurirsi.
|GH|>1, risulta allora |xf|>|xs|; chiudendo S2 e aprendo simultaneamente S1 l'oscillazione a frequenza Fo cresce in ampiezza col passare del tempo, sino a quando non intervengono fenomeni di non linearità nell'amplificatore.
Nell'ultimo caso l'oscillazione ha carettere "autoinnescante" e nasce spontaneamente nell'anello di reazione al momento della chiusura del circuito di alimentazione , rendendo superflua la funzione di eccitazione della sorgente xs.
In pratica l'autoinnesco è reso possibile dall'inevitabile presenza di una componente del rumore a frequenza Fo; tale componente, di valore infinitesimo, viene esaltata in modo esclusivo dall'anello di reazione (nel caso 3 ), mutandosi rapidamente in un'oscillazione di grande ampiezza.
Le condizioni di innesco sono pertanto:
|GH|>1 e fase di GH = 0
Le condizioni necessarie per ottenere in uscita un'oscillazione di ampiezza costante sono invece:
|GH|=1 e fase di GH = 0
queste sono note come condizioni di Barkhausen.
La necessità di soddisfare tali condizioni per un'unico valore di frequenza rende indispensabile la presenza nell'anello di reazione di componenti selettivi (elementi induttivi e capacitivi).
Al fine di ottenere l'autoinnesco dell'oscillazione, si deve prevedere nel funzionamento lineare iniziale un guadagno |GH| leggermente maggiore di 1. Successivamente, col crescere dell'ampiezza della sinusoide, la diminuzione del guadagno A dell'amplificatore dovuta a fenomeni di non linearità, riporta gradualmente il valore di |GH| a 1, con la conseguente stabilizzazione dell'ampiezza, anche se con una certa distorsione.
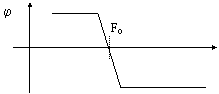
La frequenza di innesco Fo di un oscillatore coincide, come si è già detto, con la frequenza per la quale lo sfasamento j lungo l'anello di reazione risulta nullo. Ne consegue che la stabilità della frequenza di oscillazione è essenzialmente legata alla stabilità della curva di fase di GH.
Per valutare il grado di stabilità in frequenza di un oscillatore si fa riferimento al seguente coefficiente:
![]()
il cui valore
deve risultare elevato per una buona stabilità. Questo significa che la
curva di fase j(F) deve
tagliare l'asse 0° con la massima pendenza possibile (vedere figura a
lato); questo si ottiene con anelli di reazione particolarmente selettivi.
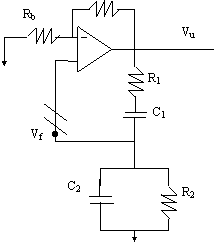
Il ponte di Wien è il circuito raffigurato in figura presenta una rete RC serie in un ramo e una rete RC parallela in un ramo adiacente. Nei due rami rimanenti vi sono due resistori.
![]()
![]()
Per la
determinazione del guadagno di anello, nelle ipotesi Ri= e Ro=0, risulta comodo aprire l'anello all'ingresso
dell'amplificatore. Lo stadio base
è un amplificatore non invertente, per il quale si ricava: Mediante
partitore sulla rete di uscita si ricava invece: con:
![]()
![]()
![]()
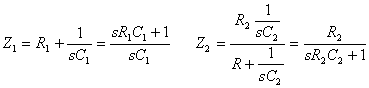 quindi:
quindi:
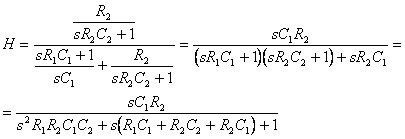
In conclusione il guadagno di anello è:
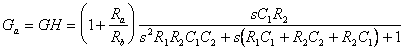
Bisogna ora verificare l'esistenza di una frequenza Fo alla quale siano verificate le condizioni di Barkhausen per l'automantenimento dell'oscillazione.
Poniamo per semplicità:
R1=R2=R
C1=C2=C
Si ottiene quindi:
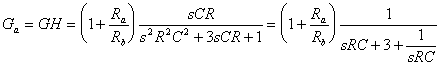
sostituiamo s=jw
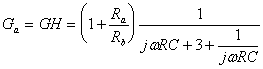
Imponendo la condizione di Barkhausen sulla fase abbiamo che dev'essere GH=0°, cioè:
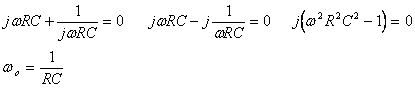
Imponendo la condizione di Barkhausen sul modulo abbiamo che dev'essere |GH|=1, cioè
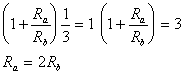
Nel caso più generale invece avremo queste condizioni:
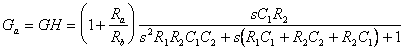
dividiamo numeratore e denominatore per sC1R2:
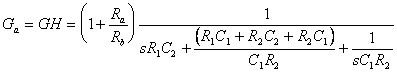
e quindi:
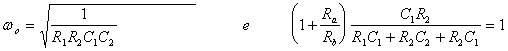
Per avere l'innesco dell'oscillazione si regola il trimmer per avere un guadagno >3, poi il guadagno viene ridotto a 3.
Il circuito visto non può essere utilizzato in pratica in quanto, non essendo presente la rete per il controllo automatico dell'ampiezza, il sistema satura o non oscilla.
Un semplice metodo per controllare automaticamente il guadagno consiste nel sostituire i resistori Ra e Rb con dei resistori sensibili alla temperatura. In particolare:
Ra ntc, Rb ptc
La prima diminuisce il proprio valore di resistenza all'aumentare della temperatura, la seconda aumenta il proprio valore di resistenza all'aumentare della temperatura. Inizialmente il guadagno dell'amplificatore è tale per cui si ha |GH|>1; in seguito, la corrente crescente che percorre Ra e Rb provoca un aumento di temperatura, quindi i valori delle resitenze si modificano come indicato sopra. In conseguenza di tali cambiamento, il guadagno di anello raggiunge il valore unitario.
E' necessario che i tempi di risposta non siano troppo lunghi (2-3 periodi della sinusoide).
Se si usa un amplificatore invertente, per avere un oscillatore la rete di reazione deve introdurre, alla frequenza di oscillazione, uno sfasamento di 180°.
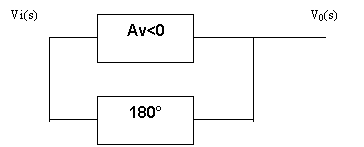
Per avere uno sfasamento di 180° la rete di reazione deve avere almeno 3 celle RC e RL (infatti ognuna ha sfasamento <=90°). Il circuito più usato è il seguente:

Se l'amplificatore ha impedenza di ingresso infinita e di uscita nulla, la funzione di trasferimento del circuito di reazione non viene influenzata dall'amplificatore. La rete ha tre condensatori e quindi la funzione di trasferimento ha tre poli. Per ω→ ∞ Vi → V0 cioè la fdt tende a 1 e quindi anche gli zeri sono tre. Per ω→ 0 i condensatori sono circuiti aperti e bloccano il segnale, si può dire che i tre zeri sono nell'origine, quindi:
![]()
ad una frequenza di 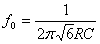 le tre celle danno uno
sfasamento di 180° e una attenuazione di
le tre celle danno uno
sfasamento di 180° e una attenuazione di ![]() , quindi per rispettare la condizione di Barkhausen deve
essere Av = - 29, come detto prima l'amplificatore deve essere
invertente. Una possibile realizzazione è:
, quindi per rispettare la condizione di Barkhausen deve
essere Av = - 29, come detto prima l'amplificatore deve essere
invertente. Una possibile realizzazione è:

Con C=15nF, R=4,3KΩ, R1=100KΩ, R2=47KΩ.
Questo circuito ha una distorsione maggiore di quella di Wien.
Oscillatore in quadratura
Permette di ottenere due segnali fra loro in quadratura e perciò viene anche chiamato oscillatore seno-coseno. Se si realizza un circuito che sfasa in anticipo di 90° e lo si mette in anello chiuso con un altro che ritarda di 90°, si realizza un circuito a reazione positiva. Se ad una certa frequenza il guadagno è uguale a 1 si ha l'oscillatore.
V0(s)

Per avere un anticipo di 90° si può usare un integratore invertente, per avere un ritardo di 90° si usa un integratore non invertente, in tale modo il guadagno unitario si ha ad una sola frequenza:
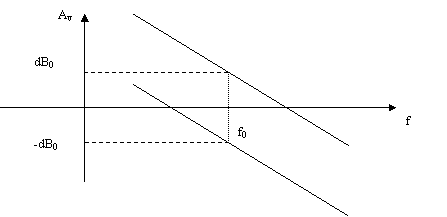
Un esempio di integratore non invertente è:
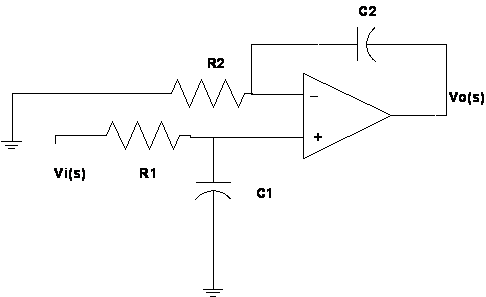
supposti gli ingressi invertente e non invertente allo stesso potenziale si ha:
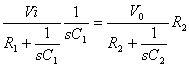
da cui ![]() nel caso in cui:
nel caso in cui: ![]() si ottiene:
si ottiene:
![]() cioè un integratore
non invertente.
cioè un integratore
non invertente.
Il circuito completo dell'oscillatore è:

Il guadagno d'anello è pari al prodotto delle funzioni di trasferimento dei due amplificatori:
![]()
Il guadagno ad anello, essendo lo sfasamento nullo a tutte le frequenze, è sempre reale. Per soddisfare Barkhausen è sufficiente che questo guadagno sia unitario. Questo si ha per:
![]() quindi
quindi ![]()
Frequentemente si pone R1C1= R2C2= R3C3=RC. Per cui:
![]()
In essi viene sfruttata la frequenza di risonanza dei circuiti LC. Vengono usati sopra i 100 kHz (tra i 100 kHz e la decina di Mhz) per difficoltà di realizzazione delle induttanze a basse frequenze. La maggior parte degli oscillatori per alte frequenze è riconducibile alla struttura a tre punti.
Lo schema di principio di un oscillatore a tre punti è presentato in fig.

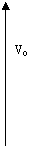
Per analizzare il circuito imponiamo alcune ipotesi semplificative:
si suppone la resistenza di ingresso dell'amplificatore Ri infinita
si suppone la resistenza Ro sufficientemente elevata da non rendere trascurabile Z3
L'amplificatore AVi ha guadagno negativo.
Valutiamo il guadagno di
anello: ![]()
Si ricava:
![]()
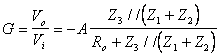
![]()
Il guadagno di anello è:

Ipotizziamo che le tre impedenze siano solo reattanze, cioè solo la componente immaginaria di Zi sia diversa da 0:
Z1=jX1 Z2=jX2 Z3=jX3 il guadagno di anello assume questa forma:
![]()
La condizione di Barkhausen sulla fase può essere verificata solo se Ga è reale, cioè se:
x1+x2+x3=0
Infatti condizione necessaria per avere fase nulla è che la parte immaginaria di Ga sia nulla, ovvero che gli elementi reattivi non siano tutti e tre dello stesso tipo (ricorda:le induttanze sono positive, le capacità negative).
Sotto questa ipotesi, il guadagno di anello diventa:
![]()
Ma questa condizione non è sufficiente: la parte immaginaria nulla si ottiene anche con una fase di 180°; per ottenere una fase di Ga pari a zero, occorre che Ga sia positivo, cioè che x2 e x3 siano concordi, e quindi elementi reattivi dello stesso tipo. Da questo segue che x1 deve essere discorde con x2 e x3.
La condizione di Barkhausen sul modulo, |GH|=1, impone che:
![]()
Fatte tutte queste premesse, si possono distinguere due tipi fondamentali di oscillatori a tre punti.
10.1.4.1 Oscillatore Hartley
Utilizza due induttori e un condensatore
(fig 10.6).

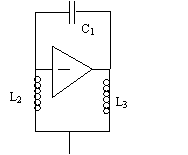
Imponendo che la fase fosse nulla abbiamo ricavato la pulsazione di oscillazione della sinusoide generata. Imponendo la condizione sul modulo otteniamo:
![]()
L'oscillatore Hartley consente di variare facilmente wo agendo soltanto sul valore della capacità C1 , senza alterare in alcun modo la condizione di oscillazione a regime che dipende esclusivamente da L2 e L3.
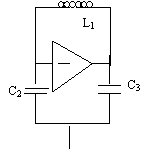

Per la condizione sul modulo otteniamo:
![]()
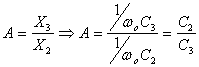
I limiti di questi oscillatori sono legati alla difficoltà di ottenere stabilmente la frequenza di oscillazione prescelta e comunque una tolleranza ristretta, cosa richiesta sempre più di frequente, si pensi ai generatori della frequenza portante nei trasmettitori e ai generatori di clock nei sistemi digitali e di telecomunicazioni. Infatti i circuiti oscillatori a risonanza hanno una stabilità in frequenza dipendente dal fattore di merito dei componenti impiegati. Più precisamente l'oscillatore risulterà tanto più stabile quanto maggiore è il coefficiente di risonanza del circuito, ovvero quanto più questi e selettivo.
Si ricorre perciò ad oscillatori al quarzo.
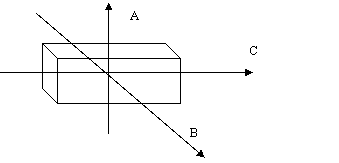
Il quarzo è un minerale costituito da biossido di silicio che presenta delle proprietà piezoelettriche. Se si provoca una leggera pressione l'ungo l'asse neutro A, si manifestano sulle due facce normali all'asse elettrico B due polarità uguali e di segno opposto, funzioni delle dimensioni della lamina e dell'entità della pressione. Si otterrà quindi l'ungo l'asse elettrico B una differenza di potenziale.
Una leggera trazione lungo l'asse neutro invece renderà evidenti sulle due facce suddette due polarità di segno opposto alle precedenti.
Una sollecitazione alternata di trazione e pressione darà origine quindi a una differenza di potenziale alternata.
Il fenomeno è perfettamente reversibile. Infatti, applicando una tensione alternata sulle facce normali all'asse elettrico B si produrrà una vibrazione.
Questo fenomeno è detto piezoelettricità.
La lamina di quarzo possiede una frequenza di risonanza fondamentale propria, funzione delle dimensioni, risonanza pochissimo smorzata per il piccolo coefficiente di attrito interno al cristallo; il quarzo è quindi schematicamente equivalente ad un circuito risonante LC ed è per questo che può essere utilizzato per creare gli oscillatori di precisione.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025