|
|
| |
![]() Probabilità di A dato B
Probabilità di A dato B
detta ![]() una partizione di
una partizione di ![]()
![]() Teorema della
probabilità totale
Teorema della
probabilità totale
Formula di Bayes per passare dalla priorità a priori a quella a posteriori
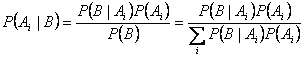
Formula di Bernoulli di ![]() successi su
successi su ![]() eventi
eventi
![]()
Funzione di distribuzione cumulativa o ripartizione di probabilità
![]() Proprietà 1)
Proprietà 1)![]() è non decrescente 2)
è continua a destra
è non decrescente 2)
è continua a destra
727c23h 727c23h 3)![]() 4)
4)![]()
727c23h 727c23h 5)
![]() 727c23h 6)
727c23h 6)![]()
Probabilità di trovarsi in un intervallo ![]()
![]()
Funzione densità di probabilità
![]() Proprietà 1)
Proprietà 1)![]() 727c23h 2)
727c23h 2)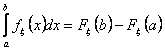
727c23h 727c23h 3)![]()
 Densità normale
Densità normale
727c23h 727c23h 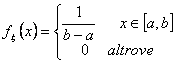
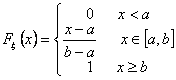
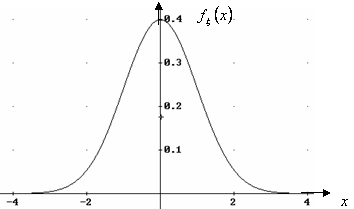
Densità normale o gaussiana (usata per modellare il rumore).
727c23h 727c23h 727c23h 727c23h 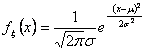
727c23h 727c23h 727c23h 727c23h 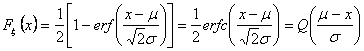
727c23h 727c23h 727c23h 727c23h 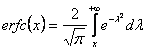
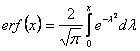
727c23h 727c23h 727c23h 727c23h ![]()
![]()
727c23h ![]() 727c23h 727c23h
727c23h 727c23h ![]() 727c23h 727c23h
727c23h 727c23h ![]()
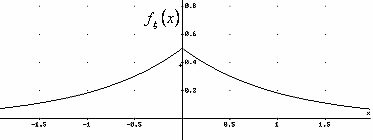
Distribuzione di Laplace che modella il segnale vocale
 727c23h 727c23h 727c23h 727c23h
727c23h 727c23h 727c23h 727c23h ![]()
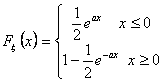
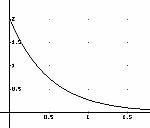
Distribuzione esponenziale che modella i guasti
 727c23h 727c23h
727c23h 727c23h 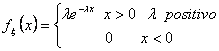
Distribuzione binomiale
![]() =# successi in un esperimento bernoulliano di
=# successi in un esperimento bernoulliano di ![]() prove
prove
![]()
![]()
Distribuzione geometrica
![]() =# di volte che devo eseguire un esperimento per avere
successo
=# di volte che devo eseguire un esperimento per avere
successo
![]()
![]()
Media o valore atteso o momento del primo ordine
![]() se continua 727c23h
se continua 727c23h ![]() se discreta
se discreta
in generale ![]()
Si definisce la varianza come la differenza tra il valore quadratico medio e la media quadratica
![]()
Funzione di distribuzione cumulativa congiunta
![]()
Le distribuzioni marginali si ricavano come segue
![]()
![]()
Densità di probabilità congiunta
![]()
se ![]() ed
ed ![]() sono statisticamente
indipendenti
sono statisticamente
indipendenti
![]()
![]()
TEORIA DELL'INFORMAZIONE
quantità di informazione associata al simbolo ![]() e si misura in bit
e si misura in bit
![]()
Entropia di informazione
![]()
![]() l'uguaglianza
vale solo nel caso di equiprobabilità
l'uguaglianza
vale solo nel caso di equiprobabilità
Un codice è univocamente decodificabile e non viola la regola del prefisso e vale la disuguaglianza di Kraft
![]()
# medio di bit
![]()
![]() se
se ![]() ossia se il # di bit
del simbolo
ossia se il # di bit
del simbolo ![]() è proprio
è proprio ![]()
TEORIA DEI SEGNALI
![]() con supporto
con supporto ![]()
si dice che ![]() è ortogonale a
è ortogonale a ![]() se
se ![]()
con ![]() detta simbolo o delta
di Kronecker
detta simbolo o delta
di Kronecker
se ![]() allora le
allora le ![]() si dicono ortronormali
si dicono ortronormali
Un segnale ![]() ad energia finita o a
potenza media finita definito su
ad energia finita o a
potenza media finita definito su ![]() si può rappresentare su
si può rappresentare su ![]() come combinazione lineare
dei segnali
come combinazione lineare
dei segnali ![]() come segue
come segue
![]() con
con ![]()
Considerazioni energetiche
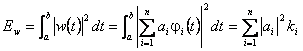 ove
ove ![]()
Un insieme di segnali è completo se l'errore quadratico medio è nullo, in formule
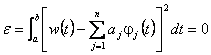
Si parte da un insieme generico di segnali ![]() a supporto su
a supporto su ![]()
Si definiscono i segnali ![]() e i segnali
e i segnali ![]() che sono
rispettivamente i segnali ortogonali e ortonormali.
che sono
rispettivamente i segnali ortogonali e ortonormali.
1° segnale) ![]()
![]()
![]()
2° segnale) ![]() 727c23h
727c23h ![]()
![]()
727c23h dove
![]() è la proiezione di
è la proiezione di ![]() su
su ![]()
![]() ° segnale)
° segnale) ![]()
![]()
![]()
727c23h dove
![]() è la proiezione di
è la proiezione di ![]() su
su ![]()
![]() segnale ad energia
finita o a potenza media finita su
segnale ad energia
finita o a potenza media finita su ![]()
sia ![]() la base di Fourier,
allora
la base di Fourier,
allora ![]() si può scrivere come
segue
si può scrivere come
segue
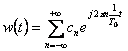 con
con 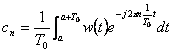 si ricorda che
si ricorda che ![]()
se ![]() è reale il suo
sviluppo in serie è reale e i coefficienti sono generici con
è reale il suo
sviluppo in serie è reale e i coefficienti sono generici con ![]()
se ![]() è reale e pari il suo
sviluppo in serie è reale e anche i coefficienti, dove
è reale e pari il suo
sviluppo in serie è reale e anche i coefficienti, dove ![]()
se ![]() è reale e dispari il
suo sviluppo in serie è reale e i coefficienti immaginari puri, dove
è reale e dispari il
suo sviluppo in serie è reale e i coefficienti immaginari puri, dove ![]()
per l'energia del segnale si ha 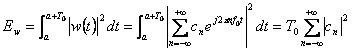
![]() 727c23h
727c23h ![]()
Proprietà della Trasformata di Fourier F
F![]()
F![]()
F![]()
F![]()
F![]()
F![]()
F![]()
F![]()
Se ![]() è reale pari
è reale pari ![]() è reale
è reale
Se ![]() è reale dispari
è reale dispari ![]() è immaginaria pura
è immaginaria pura
Definizioni della ![]() di Dirac:
di Dirac: ![]() 727c23h 727c23h
727c23h 727c23h ![]()
727c23h 727c23h ![]() 727c23h
727c23h ![]()
727c23h 727c23h ![]() 727c23h 727c23h
727c23h 727c23h ![]()
Prodotto di convoluzione
![]()
Energia di un segnale ![]() definito su
definito su ![]()
![]()
Densità spettrale di energia : ![]()
Teorema di Parseval (per i segnali ad energia finita e a potenza media finita) che mi dice che trasformando o sviluppando in serie di Fourier io non perdo alcuna informazione sul segnale
![]() oppure
oppure ![]()
Formulazione generale del Teorema di Parseval per segnali ad energia finita (o periodici a potenza media finita)
![]() se
se![]() allora
allora ![]()
Potenza media (normalizzata) di un segnale ![]()
![]()
![]() è reale,
non negativo e pari
è reale,
non negativo e pari
![]() potenza
normalizzata
potenza
normalizzata
Se ![]() è periodico si può
scrivere come
è periodico si può
scrivere come
![]() e
e ![]()
posto ![]() allora
allora ![]()
quindi ![]() da cui
da cui ![]()
allora la potenza di
![]() si esprime come
si esprime come ![]()
ed il suo spettro di
potenza come ![]()
Se la grandezza in esame è una potenza allora
il decibel è ![]()
Se la grandezza in esame è una tensione o una
corrente allora il decibel è ![]()
Si definisce decibel al milliwatt ![]()
Formula trigonometrica di Eulero ![]()
TEORIA DEI SISTEMI
Un sistema è lineare se ad una combinazione lineare degli ingressi corrisponde una combinazione lineare delle uscite.

Un sistema si dice tempo invariante o invariante
per traslazioni temporali se l'uscita ![]() ritardata di una
quantità
ritardata di una
quantità ![]() coincide con l'uscita
coincide con l'uscita ![]() ottenuta inviando in
ingresso il segnale
ottenuta inviando in
ingresso il segnale ![]() ritardato della stessa
quantità.
ritardato della stessa
quantità.
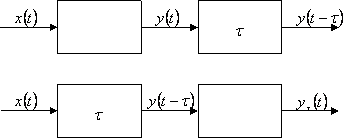
La risposta all'impulso caratterizza un sistema LTI (Linear Time Invariant)
![]() dove
dove![]() è la risposta del sistema LTI quando all'ingresso c'è
è la risposta del sistema LTI quando all'ingresso c'è ![]()
facendo la trasformata di Fourier
![]() dove
dove ![]() è detta funzione di
trasferimento
è detta funzione di
trasferimento
Densità Spettrale di Energia dell'ingresso
![]()
Densità Spettrale di Energia dell'uscita
![]()
Un sistema LTI è non distorcente se il modulo
dell'uscita è costante e la fase varia in maniera lineare con ![]()
Scritto ![]()
![]() lineare con
lineare con ![]()
![]() lineare con
lineare con ![]()
PROCESSI CASUALI
Stazionario dell'![]() ordine
ordine
![]()
Stazionario del primo ordine
![]()
Un processo casuale (p.c.) che dipende dal tempo in maniera periodica è detto ciclostazionario
Media temporale di un p.c. ![]()
p.c. stazionari
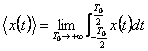
 Media statistica o media di insieme di un p.c.
Media statistica o media di insieme di un p.c. ![]()
![]()
p.c. ergodici
Se un p.c. stazionario è tale che
![]() il processo si dice
ergodico
il processo si dice
ergodico
![]()
se il p.c. è stazionario del secondo ordine la
media congiunta non dipende dal tempo, posto ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Spettro di potenza di un segnale numerico sotto l'ipotesi di stazionarietà
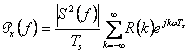 con
con![]() e
e ![]() simbolo
simbolo ![]()
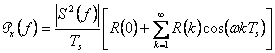
NRZ (non return to zero)

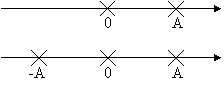 727c23h 727c23h NRZ
unipolare
727c23h 727c23h NRZ
unipolare
727c23h 727c23h NRZ antipodale
RZ (return to zero) ![]() è detto duty cycle
è detto duty cycle

 727c23h 727c23h RZ
unipolare
727c23h 727c23h RZ
unipolare
727c23h 727c23h RZ antipodale
PARAMETRI CHE CARATTERIZZANO UN SISTEMA DI TRASMISSIONE
![]() è la velocità di
trasmissione espressa in
è la velocità di
trasmissione espressa in ![]()
![]() è la velocità di
segnalazione espressa in
è la velocità di
segnalazione espressa in ![]()
![]() è la banda
(unilatera) occupata dal segnale espressa
in
è la banda
(unilatera) occupata dal segnale espressa
in ![]()
![]() è l'efficienza espressa
in
è l'efficienza espressa
in ![]()
|
SEGNALE |
|
|
|
|
|
NRZ binario |
|
|
|
|
|
RZ (50%) binario |
|
|
|
|
|
NRZ quaternario |
|
|
|
|
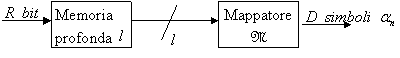
727c23h 727c23h 727c23h 727c23h 727c23h ![]()
INTERFERENZA INTERSIMBOLICA (ISI)
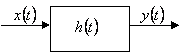 727c23h 727c23h
727c23h 727c23h ![]() 727c23h
727c23h ![]()
727c23h posto ![]() segue
segue ![]()
727c23h detto
![]() l'istante di
campionamento
l'istante di
campionamento 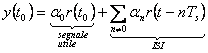
Distorsione di picco
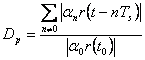 con
con ![]()
![]() è minima. Bisogna che
è minima. Bisogna che ![]() altrimenti si hanno
errori sistematici
altrimenti si hanno
errori sistematici
Primo teorema di Nyquist che ci dice come deve comportarsi la trasformata di Fourier di un segnale elementare affinché questo segnale elementare ci assicuri ISI nulla.
![]() dove
dove ![]() è il segnale
elementare
è il segnale
elementare
SEGNALE A COSENO RIALZATO
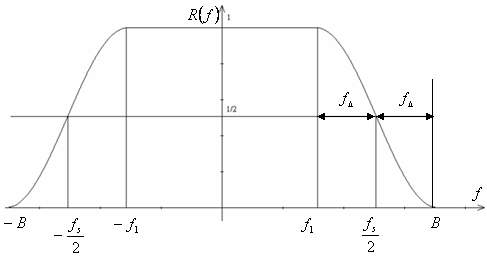
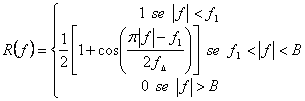 con
con ![]() e
e ![]()
graficamente:
![]() è la banda minima
è la banda minima
![]() inizio e fine raccordo
inizio e fine raccordo
![]() banda totale
(unilatera)
banda totale
(unilatera)
Coefficiente di ROLL-OFF
![]() rapporto tra la
banda aggiuntiva
rapporto tra la
banda aggiuntiva ![]() e la banda minima
richiesta
e la banda minima
richiesta ![]()
se ![]() è zero mi trovo nel
caso di una porta e non ho banda aggiuntiva, se
è zero mi trovo nel
caso di una porta e non ho banda aggiuntiva, se ![]() è uno vuol dire che ho
è uno vuol dire che ho
![]()
quindi ![]() . Conoscendo
. Conoscendo ![]() si calcola
si calcola ![]() come
come
![]() detta
detta ![]() la velocità do
segnalazione in
la velocità do
segnalazione in ![]() e
e ![]() segue
segue
![]() ossia
ossia ![]() e se ho una banda
e se ho una banda ![]() , siccome
, siccome ![]() segue che
segue che ![]()
![]()
IL RUMORE
Sia ![]() un p.c. stazionario,
ergodico, gaussiano, la densità spettrale del suo valore quadratico medio vale
un p.c. stazionario,
ergodico, gaussiano, la densità spettrale del suo valore quadratico medio vale
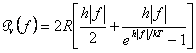 con
con ![]() in
in ![]() ,
, ![]() è la costante di Plank
è la costante di Plank
727c23h 727c23h ![]() è la costante di
Boltzman
è la costante di
Boltzman
Se ci si trova ad operare con ![]() e
e ![]() allora l'espressione
del valore quadratico medio di
allora l'espressione
del valore quadratico medio di ![]() si approssima come
si approssima come ![]()
![]() è la potenza
disponibile (siamo in situazione di adattamento) che si distribuisce a valle e
vale
è la potenza
disponibile (siamo in situazione di adattamento) che si distribuisce a valle e
vale

![]() (N.B. la resistenza
non ha pedice perchè siamo in adattamento)
(N.B. la resistenza
non ha pedice perchè siamo in adattamento)
La densità spettrale della potenza di rumore termico disponibile di una resistenza
a vuoto sarà
![]() con
con ![]() che è la potenza di rumore
che è la potenza di rumore
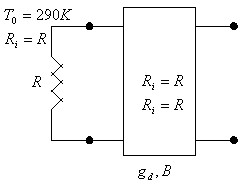 CIFRA DI RUMORE
CIFRA DI RUMORE

Il sistema è lineare
e supponiamo il guadagno ![]() costante
costante

Notare che ![]() è costante perchè
generato internamente al bipolo.
è costante perchè
generato internamente al bipolo.
Integrando sulla
banda si ha per ![]() la seguente
espressione
la seguente
espressione
 dove
dove ![]() è la potenza di rumore
disponibile all'uscita.
è la potenza di rumore
disponibile all'uscita.
 Nel caso in cui il doppio bipolo fosse una
linea si ha che
Nel caso in cui il doppio bipolo fosse una
linea si ha che ![]() ,ossia la cifra di rumore coincide con l'attenuazione della linea.
,ossia la cifra di rumore coincide con l'attenuazione della linea.
Riepilogando:la cifra di rumore è il rapporto tra la densità spettrale della potenza di rumore all'uscita del doppio bipolo e la densità spettrale della potenza di rumore alluscita del doppio bipolo ne caso che il doppio bipolo non introduca rumore.
![]() questa è la
definizione operativa di cifra di runore.
questa è la
definizione operativa di cifra di runore.
![]() per convenzione.
per convenzione.
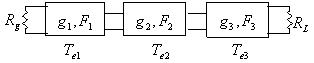 Si ha
Si ha ![]()
Essendo ![]() il termine che tiene
conto della generazione interna
il termine che tiene
conto della generazione interna
di rumore del doppio bipolo. Si vede facilmente che
![]() e che
e che ![]()
Cifra di rumore
equivalente e temperatura equivalente di una cascata di ![]() doppi bipoli
doppi bipoli
![]()
![]()
![]()
CANALE HERTZIANO
La potenza ricevuta è
![]()
Con ![]() guadagno dell'antenna ricevente e
guadagno dell'antenna ricevente e ![]() guadagno dell'antenna
trasmittente
guadagno dell'antenna
trasmittente
![]() guadagno di
propagazione nello spazio libero
guadagno di
propagazione nello spazio libero
![]() potenza trasmessa
potenza trasmessa
![]() è la lunghezza d'onda
ed
è la lunghezza d'onda
ed ![]() è la frequenza a cui
stiamo operando
è la frequenza a cui
stiamo operando
![]() è la distanza tra le
due antenne
è la distanza tra le
due antenne
Detta ![]() la densità spettrale
della potenza di rumore disponibile all'ingresso di un canale, la densità
spettrale della potenza di rumore disponibile all'uscita dello stesso canale
sarà
la densità spettrale
della potenza di rumore disponibile all'ingresso di un canale, la densità
spettrale della potenza di rumore disponibile all'uscita dello stesso canale
sarà ![]()
Ossia ![]()
Un processo casuale gaussiano è detto bianco o non colorato, quando non
dipende dalla frequenza, ossia quando la sua densità spettrla edi potenza è
costante e vale per convenzione ![]() , il fattore ½ tiene conto del fatto che le bande in genere
sono unilatere.Con
, il fattore ½ tiene conto del fatto che le bande in genere
sono unilatere.Con ![]()
PROBABILITA' DI ERRORE SUL SIMBOLO E SUL BIT (2-ASK, BPSK, 2-PSK)
 Detta
Detta ![]() la quantità in figura,
la probabilità di errore di un simbolo vale
la quantità in figura,
la probabilità di errore di un simbolo vale 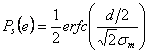
 CASO NRZ ANTIPODALE BINARIO
CASO NRZ ANTIPODALE BINARIO
![]() con
con ![]() banda del segnale
(unilatera) ed
banda del segnale
(unilatera) ed ![]() come già definito
come già definito
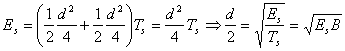
Si ha 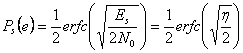 dove
dove ![]() è il rapporto segnale
rumore
è il rapporto segnale
rumore ![]() (all'uscita). Se il
segnale è binario si ha
(all'uscita). Se il
segnale è binario si ha ![]() , ossia la probabilità di errore sul simbolo coincide con
quella sul bit, quindi
, ossia la probabilità di errore sul simbolo coincide con
quella sul bit, quindi ![]() e
e 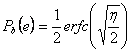 con
con ![]() . Si userà l'espressione più adatta in base al contesto.
. Si userà l'espressione più adatta in base al contesto.
![]() con
con ![]() banda del segnale
(unilatera) ed
banda del segnale
(unilatera) ed ![]() come già definito
come già definito

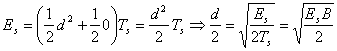
A
Si ha 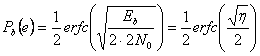 dove
dove ![]() è il rapporto segnale
rumore
è il rapporto segnale
rumore ![]() (all'uscita). Siamo
nel caso di segnale è binario.
(all'uscita). Siamo
nel caso di segnale è binario.
Notare che a causa della presenza della ![]() nel mezzo della banda
l'energia del segnale è dimezzata.
nel mezzo della banda
l'energia del segnale è dimezzata.
FILTRO ADATTATO (esalta il segnale ma non il rumore)
Sia ![]() un segnale ed
un segnale ed ![]() un p.c. (rumore)
un p.c. (rumore)
Le ipotesi sono:
![]() è limitato nel tempo,
es.
è limitato nel tempo,
es. ![]()
![]() è nota
è nota
Segue che il filtro adattato ha la seguente Funzione di Trasferimento (FdT)
![]() Si ha
Si ha 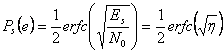 dove
dove ![]()
Quindi utilizzando
un filtro adattato ho un guadagno di ![]() , perché a parità di probabilità uso metà energia ovvero a
parità di energia dimezzo la probabilità di errore.
, perché a parità di probabilità uso metà energia ovvero a
parità di energia dimezzo la probabilità di errore.
4-ASK

Probabilità di errore sul simbolo in una costellazione equispaziata (indipendente dal segnale elementare).
Per i segnali alle
estremità vale 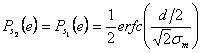 (una sola coda
accavallata)
(una sola coda
accavallata)
Per i segnali
centrali invece vale 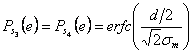 (entrambe le code
accavallate)
(entrambe le code
accavallate)
La probabilità
media vale invece 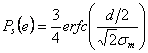 , in generale, con costellazioni equispaziate di
, in generale, con costellazioni equispaziate di ![]() simboli si ha
simboli si ha 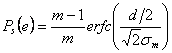 . La probabilità di errore sul bit si ricava, nota
. La probabilità di errore sul bit si ricava, nota ![]() , come
, come ![]() , con
, con ![]() numero dei simboli.
numero dei simboli.
Probabilità di errore sul simbolo in una costellazione equispaziata (segnale NRZ antipodale).
Fissata l'origine
tra ![]() ed
ed ![]() , l'energia media
, l'energia media 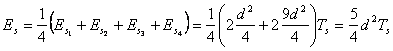 , da cui
, da cui 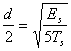 e quindi
e quindi 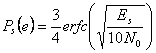 .
.
Siccome ![]() e
e ![]() si ha.
si ha.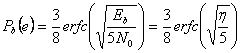
INVILUPPO COMPLESSO
![]() , con
, con ![]() pulsazione istantanea,
pulsazione istantanea,
![]() segnale modulato,
reale, la cui
segnale modulato,
reale, la cui ![]() è centrata in 0
è centrata in 0
La densità
spettrale di potenza di ![]() si può scrivere come
si può scrivere come
![]() , notare che
, notare che ![]() può essere complesso
può essere complesso
MODULAZIONE DI AMPIEZZA
![]() 727c23h :segnale
modulante.
727c23h :segnale
modulante.
![]() :segnale
di portante
:segnale
di portante
![]() :segnale
modulato
:segnale
modulato
In questo caso ![]() e quindi
e quindi ![]()
Efficienza 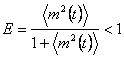 . Per
l'utilizzo di un demodulatore coerente deve essere
. Per
l'utilizzo di un demodulatore coerente deve essere ![]()
PROBABILITA' DI ERRORE DI UN 4-PSK
Detta ![]() la probabilità di
errore sul simbolo e sul bit di un BPSK si ha in generale
la probabilità di
errore sul simbolo e sul bit di un BPSK si ha in generale
![]() 727c23h
727c23h ![]()
ma se il demodulatore del 4-PSK è composto di due demodulatori BPSK indipendenti si ha:
![]() 727c23h
727c23h ![]() e quindi il BPSK ed il
4-PSK hanno la stessa probabilità di errore sul bit.
e quindi il BPSK ed il
4-PSK hanno la stessa probabilità di errore sul bit.
PROBABILITA' DI ERRORE DI UN 16-QAM
![]()
NUMERO MEDIO DI RITRASMISSIONI IN UN SISTEMA CON CRC
![]() dove
dove ![]() indica la probabilità
di ritrasmettere
indica la probabilità
di ritrasmettere
PCM
Canale BSC con
probabilità di errore ![]() , quantizzatore con
, quantizzatore con ![]() bit
bit
Livelli di
quantizzazione ![]()
![]() passo di
quantizzazione
passo di
quantizzazione
![]() potenza associata
all'errore di quantizzazione
potenza associata
all'errore di quantizzazione
![]() potenza di segnale
all'uscita del quantizzatore
potenza di segnale
all'uscita del quantizzatore
![]() rapporto segnale
rumore all'uscita del quantizzatore, numero puro
rapporto segnale
rumore all'uscita del quantizzatore, numero puro
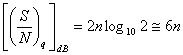 rapporto
segnale rumore all'uscita del quantizzatore in
rapporto
segnale rumore all'uscita del quantizzatore in ![]()
![]() rapporto
segnale rumore all'ingresso del quantizzatore, numero puro
rapporto
segnale rumore all'ingresso del quantizzatore, numero puro
![]() potenza associata
all'errore sul bit in trasmissione
potenza associata
all'errore sul bit in trasmissione
![]() rapporto
segnale rumore massimo all'ingresso del ricevitore
rapporto
segnale rumore massimo all'ingresso del ricevitore
![]() rapporto segnale
rumore medio all'ingresso del ricevitore
rapporto segnale
rumore medio all'ingresso del ricevitore
in ![]() ed in corrispondenza
di
ed in corrispondenza
di ![]() vale
vale ![]()
![]() relazione tra
massimo e medio
relazione tra
massimo e medio
![]() rapporto segnale
rumore sul bit all'uscita del canale BSC
rapporto segnale
rumore sul bit all'uscita del canale BSC
![]() 727c23h rapporto
segnale rumore sul bit all'uscita del canale BSC in
727c23h rapporto
segnale rumore sul bit all'uscita del canale BSC in ![]()
![]() è la probabilità di
soglia che si ricava ugluagliando
è la probabilità di
soglia che si ricava ugluagliando ![]() e
e ![]() ottenendo
ottenendo
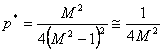 valore della
probabilità di soglia
valore della
probabilità di soglia
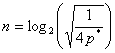 è il numero
massimo di bit del quantizzatore per un afissata
è il numero
massimo di bit del quantizzatore per un afissata ![]()
Dato il guadagno ![]() in
in ![]() , allora si può scrivere
, allora si può scrivere 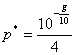
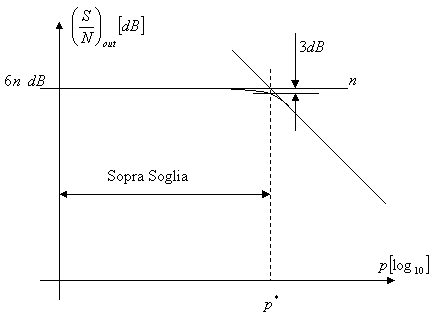
Se ![]() aumenta
aumenta ![]() si sposta a sinistra e
viceversa.
si sposta a sinistra e
viceversa.
Rapporto segnale
rumore all'ingresso del ricevitore 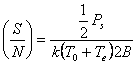 dove:
dove:
![]() è la costante
di Boltzmann
è la costante
di Boltzmann
![]() è la potenza di
segnale all'ingresso della linea
è la potenza di
segnale all'ingresso della linea
![]() questo fattore è
dovuto alla modulante che è una sinusoide
questo fattore è
dovuto alla modulante che è una sinusoide
Il rapporto segnale
rumore all'uscita del demodulatore raddoppia o in ![]() si somma 3
si somma 3
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026