|
|
| |
FORMULA DI BLACKMAN
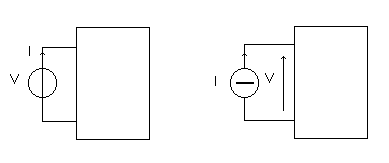
Consideriamo il caso in cui ci interessi valutare l'impedenza che si osserva tra due morsetti di una rete. Per fare ciò posso applicare un generatore di tensione di prova e valutare la corrente che esso eroga oppure, in modo analogo, applicare un generatore di corrente di prova e valutare la tensione che si osserva ai suoi capi.
Supponiamo ora che il sistema con cui abbiamo
a che fare sia un sistema reazionato. A seconda dei tipi di reazione posso
assumere che la grandezza di ingresso sia una tensione e la grandezza di uscita
una corrente, o viceversa, ma in ogni caos che si può analizzare, la funzione
di trasferimento, per quanto visto prima avrà sempre la forma: ![]() .
.
Al denominatore comparirà sempre il guadagno d'anello.
Ora, a secondo delle grandezze scelte noi possiamo avere due tipi di funzioni:
I = f (V) oppure V = g (I)
Le due funzioni di trasferimento Xo/Xs , a seconda dei due casi prima esposti, avranno rispettivamente la dimensione di una resistenza e di una conduttanza, denomina 919i83j te:
Rif e 1/Rif
Dove la F sta per feedback.
Ovviamente i due valori sono legati dal fatto che uno non è altro che l'inverso dell'altro.
La formula di Blackman ci permette di calcolare la Rif nel seguente modo:
![]()
Vediamo come calcolare i vari termini nel caso dell'amplificatore di tensione:
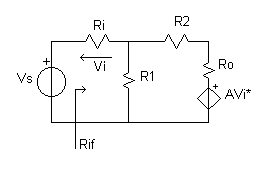
La Rid, è la resistenza di sistema morto, ed è la resistenza che si osserva in ingresso quando si annulla il generatore pilotato, quindi nel nostro caso sarà:
![]()
Toc, vale Vi/Vi* quando tra i due morsetti c'è una circuito aperto (OC = OPEN CIRCUIT), equivale quindi a togliere il generatore Vs. In questo caso si vede che la Vi è nulla in quanto in Ri non circola corrente e quindi in questo circuito si ha:
Toc = 0
Tsc, vale Vi/Vi* quando tra i due morsetti vi è un cortocircuito (SC = SHORT CIRCUIT), bisogna quindi cortocircuitare Vs. SI ha quindi:
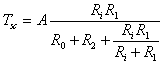
In definitiva, quindi si ha:
![]()
Sarei arrivato ad un analogo risultato facendo i conti utilizzando il generatore di prova.
ANALISI IN FREQUENZA DI AMPLIFICATORI REAZIONATI.
Quando si deve fare un progetto o valutare in prima approssiamzione cosa succede in un circuito , possono essere utili le formule ricavate in via generale per sistemi reazionati, e in particolare la formula che esprime il guadagno ad anello chiuso:
![]()
con G guadagno ad anello aperto e H reazione.
Questo approccio approssimato è particolarmente utile nell'analisi in frequenza di amplificatori reazionati.
Possiamo avere amplificatori a larga banda, cioè dotati sia di frequenza di taglio inferiore che di frequenza di taglio superiore o amplificatori operazionali che posseggono solo una frequenza di taglio superiore, a sua volta poi questi ultimi amplificatori possono avere uno o più poli che identificano la pendenza della curva dopo il taglio.
Iniziamo con l'analisi dell'amplificatore a larga banda.
AMPLIFICATORE A LARGA BANDA
La curva di risposta di un amplificatore a larga banda ha il seguente andamento:
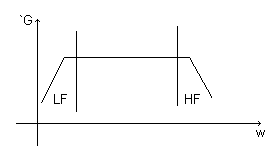
Il guadagno G avrà la seguente forma: ![]()
Nella zona di guadagno piatto è come se nel circuito non ci fossero elementi reattivi, quindi non ha senso fare uno studio in frequenza in questa zona, possiamo invece analizzare cosa succede a basse e ad alte frequenze:
BASSE FREQUENZA: vediamo cosa succede applicando la reazione:
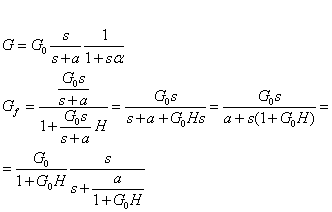
Come si vede da quanto scritto, la reazione fa si che: ad una diminuzione di guadagno, corrisponda una equivalente diminuzione della frequenza di taglio inferiore.
Ciò equivale a dire che il polo si sposta sempre più verso lo zero sul polo delle redici.
ALTE FREQUENZA: analogamente a prima ptteniamo:
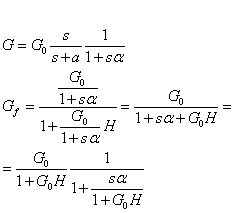
Ancora, otteniamo che: diminuendo il guadagno si alza la frequanza di taglio superiore.
CONCLUSIONI: DIMINUENDO IL GUADAGNO SI AUMENTA LA BANDA PASSANTE.
Sul luogo delle radici ciò equivale ad uno spostamento delle radici verso gli zeri.
NOTA: La reazione sposta solo i poli e non gli zeri.
AMPLIFICATORE OPERAZIONALE
Consideriamo un amplificatore per continua con due poli, con la seguente curva di risposta:
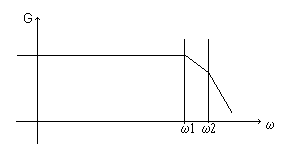
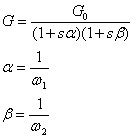
Come prima andiamo a vedere cosa succede quando applichiamo una reazione:
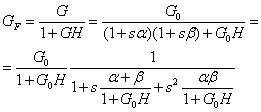
Il sistema reazionato presenta ancora due poli, in generale questi due poli sono complessi coniugati.
Il denominatore dell'espressione trovata ha la seguente forma:
![]()
dove Q viene detto FATTORE DI MERITO e K FATTORE DI SMORZAMENTO.
Nel caso in cui K<![]() o equivalentemente Q>
o equivalentemente Q>![]() la Gf presenta una massimo.
la Gf presenta una massimo.
Consideriamo ora un caso particolare:
studiamo la funzione quando il rapporta tra i due poli è pari al guadagno ad
anello alle basse frequenze; cioè : ![]() .
.
Otteniamo la seguente espressione:
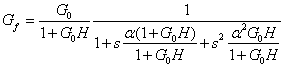
Se ipotizziamo che GoH >>1 allora possiamo scrivere:
![]()
Confrontando il denominatore di questa
espressione con la forma generale prima riportata, si ottiene che in questo
caso particolare![]() ; quindi il polo più alto ha la stessa pulsazione della frequenza di
oscillazione non smorzata. Inoltre, si ha che Q=1 e quindi K=0.5, e allora per
quanto detto la funzione presenta un massimo di
; quindi il polo più alto ha la stessa pulsazione della frequenza di
oscillazione non smorzata. Inoltre, si ha che Q=1 e quindi K=0.5, e allora per
quanto detto la funzione presenta un massimo di ![]() dB=1,25 dB rispetto al guadagno a basse frequenze.
dB=1,25 dB rispetto al guadagno a basse frequenze.
In generale, per un sistema del secondo ordine quale è questo possiamo riassumere le seguenti caratteristiche:
Se il rapporto ![]() > 4GoH ho due poli reali, per 2GoH<
> 4GoH ho due poli reali, per 2GoH<![]() < 4GoH i poli sono complessi coniugati ma non vi è un massimo e
infine per GoH <
< 4GoH i poli sono complessi coniugati ma non vi è un massimo e
infine per GoH < ![]() < 2GoH ho due poli complessi coniugati con massimo.
< 2GoH ho due poli complessi coniugati con massimo.
Un sistema del secondo ordine, lo posso ottenere anche attraverso una rete RLC, come segue:
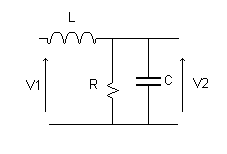
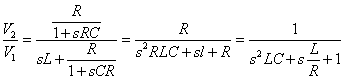
Ma una funzione identica la si può ottenere anche con una rete RC in retroazione, com visto prima.
Questo è un aspetto molto importante, in quanto significa che io posso inserire nei circuiti coppie di poli complessi coniugati, senza dover far ricorso alle induttanze che sono elementi molto poco precisi.
CRITERI DI STABILITÀ PER UN SISTEMA IN ANELLO CHIUSO.
Esistono vari criteri per analizzare la stabilità di un sistema ad anello chiuso. Noi analizzaremo i due principali criteri:
CRITERIO DI NYQUIST
CRITERIO DI BODE
Il primo dei due criteri è quello che meglio fornisce informazioni sulla stabilità ma, in pratica, viene più spesso utilizzato il criterio di Bode che è di più facile utilizzo.
CRITERIO DI NYQUIST
Il criterio fondamentale è che i poli della funzione di trasferimento ad anello chiuso devono trovarsi tutti nel semipiano s<0. (Ad esempio l'integratore non è stabile in quanto ha un polo nell'origine).
Analizziamo quale è la forma di una funzione di trasferimento ad anello chiuso.
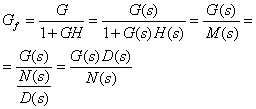
Supponiamo, come è possibile fare , che sia G(s) che H(s) abbiano tutti i loro poli con parte reale negativa, cioè che siano blocchi stabili, allora la stabilità della Gf , dipende totalmente dagli zeri della funzione 1+G(s)H(s), che sono poi i poli della Gf.
Quindi 1+G(s)H(s) non deve avere zeri (o poli) con parte reale positiva.
Vediamo ora come valutare il numero di zeri con parte reale positiva.
Dalla differenza tra gli zeri e i poli, si può rilevare quanti giri fa una curva che racchiude nel dominio tali poli e zeri.
Se consideriamo qualunque contorno chiuso del semipiano positivo del dominio, vogliamo che nell'immagine il contorno non circondi l'origine, perchè vogliamo zeri solo nel semipiano destro.
Studiamo allora M(s) in un contorno nel semipiano destro:
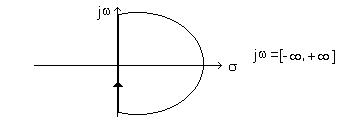
Tracciamo il diagramma polare di G(jw)H(jw); se il diagramma comprende al suo interno il punto (-1,0), detto PUNTO DI NYQUIST, il sistema è instabile, se non lo comprende il sistema è stabile.
Introduciamo a questo punto i concetti di margine di fase e margine di guadagno:
Tracciamo sul diagramma polare della funzione, un cerchio di raggio unitario, esso passa per il punto di Nyquist e intersecherà il diagramma polare, tracciamo un semiretta che congiunge l'origine e quisto punto di intersezione che è individuato da una frequenza wc ;definiamo il MARGINE DI FASE come l'angolo formato da questa semiretta e il semiasse reale negativo, quindi:
Mj= arg (Ga(jwc
Perchè un sistema sia stabile, il margine di fase deve essere positivo
Un sistema si dice INGEGNERISTICAMENTE STABILE se il margine di fase è maggiore di 45°.
Consideriamo ora, sempre sul diagramma precedente, in cui abbiamo tracciato il cerchio di raggio unitario, l'intersezione del diagramma polare con il semiasse reale negativo.
Il sistema è stabile se questa intersezione è allinterno del cerchio.
Si definisce MARGINE DI GUADAGNO la seguente grandezza:
Mg = - | GH | arg (GH) = 180 °
Se Mg è negativo l'intersezione dsta nel cerchio, viceversa sta fuori.
CRITERIO DI BODE
Per il criterio di Bode, un sistema è stabile se il modulo di GH taglia l'asse delle w a 0 dB sul diagramma di Bode del modulo con una pendenza non superiore a -20 dB/dec.
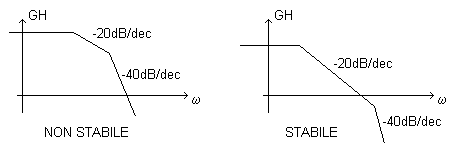
Nel caso particolare, in cui il diagramma arriva sull'asse con una pendenza di -20db/dec e continui dopo con una pendenza di -40dB/dec, siamo nel caso intermedio in cui il margine di fase vale 45°..
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025