RUMORE TERMICO

tecnica

RUMORE TERMICO

Poiché è dovuto al sommarsi (sovrapporsi) di un numero estremamente grande di fenomeni (eventi caotici tutti dello stesso tipo) quasi indipendenti tra loro, il modello per esso corretto è quello di un processo gaussiano, che sarà inoltre anc 858j91i he ergodico e stazionario (SSL SSS).

In ogni istante quindi il segnale sarà una variabile aleatoria N(t) che potrà assumere valori con una densità di probabilità del tipo:

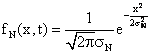
Avrà quindi valor medio nullo e varianza . Tenendo conto anche dell'ergodicità potremo scrivere:

E, dalla definizione di potenza di un processo:

Analizzando la correlazione tra i valori del rumore in due istanti distinti t₁ e t₂, per la stazionarietà del processo otterremo una funzione di autocorrelazione dipendente solo dalla distanza t=t₂-t₁, R_NN(t). Poiché abbiamo detto che le cause caotiche del rumore sono molto poco correlate, la R_NN(t) sarà quasi nulla per t>0 ed assumerà valori significativi per istanti molto vicini allo 0.

Tenendo conto, con opportuni modelli, di queste correlazioni e del fatto che le densità di probabilità del secondo ordine sono congiuntamente gaussiane, si ottiene per la R_NN(t

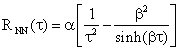
Con a e b parametri dipendenti dalla temperatura, dalla costante di Boltzmann, dalla costante di Planck e dalla natura del sistema rumoroso.

Avremo anche che:

Ad esempio, nel caso di una resistenza elettrica R, considerando il rumore in tensione, si ha:

    (con h=cost.di Planck, K=cost.di Boltz.,T=temp.)

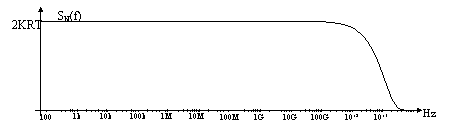La trasformata di Fourier dell'autocorrelazione ci darà lo spettro di densità di potenza, che è pari a:

E nel caso della resistenza:

che ha  e decresce di 3dB in corrispondenza di , quindi è praticamente piatta per quasi tutte le frequenze di utilizzo fisico reale. Per questo si suppone che il rumore sia anche bianco e cioè lo si modellizza con una: