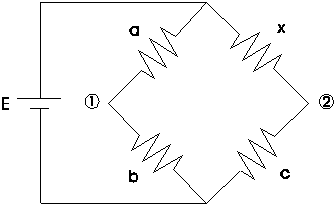
dove è possibile variare grossolanamente i valori di a e di b, mentre c è il campione finemente variabile. Lo scopo di variare a , b e c è di annullare la tensione ai capi del galvanometro (che è posto fra i nodi 1 e 2), così che:

V_G =V₁₂= 0 =>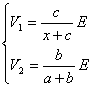

da cui: 

di conseguenza leggendo i valori di a , b e c quando V_G = 0 siamo in grado di determinare il valore 757i87h di x. 

APPARECCHIATURE USATE

Cassetta di resistori Allocchio Bacchini & C

mod 1548 inv. Nº 2559

2x5 valori da 1 a 10000 W

potenza dissipata per ogni bobina: 2 W a carico continuo

taratura eseguita a 0.02%

Decade Resistor Decabox

Type 1434_N, serial 9749, inv. Nº2736

Incertezza: (0.02% + 5mW

Coefficiente di temperatura: < 10 ppm / ºC a temperatura ambiente; per bassi valori di resistenza è necessario aggiungere 0.4% / ºC.

Tolleranze in corrente continua:

Resistenze da misurare

Scatolini R2 di resistori con resistenze nominali pari a 10W W W W ; incertezza nominale 5% ; potenza nominalmente dissipabile 5W ; coefficiente di temperatura 200 ppm/K

Galvanometro

Type 2707, inv. Nº 2762

Max sensitivity: 10 mV    (1 nA)

Max input : 5 V

Resistenza di ingresso 9 kW

Interruttore SEB

Mod T/S n^o 720826, inv Nº 2616

Interruttore a coltelli

Inv Nº 2328

DC power supply HP E3611A

Inv Nº 3097

Tensione di uscita massima 35 V

ESECUZIONE DELLA MISURAZIONE

Abbiamo eseguito una misurazione per tre dei quattro resistori a disposizione.

x = 10 W

Il valore nominale della resistenza è: x_n = 10 W

Occorre scegliere il valore da assegnare:  - alla tensione di alimentazione E

alle resistenze a, b e c

in modo da ottenere un compromesso ottimale tra precisione, sensibilità e risoluzione.

Poiché a e b possiedono un'incertezza pari a 2 10^-4, è bene scegliere c in modo da non peggiorare tale accuratezza. In questo caso dunque:

ovvero devo poter agire sui mW di x.

Poiché la minima variazione possibile di c è pari a 0.1 W

Ne consegue che c = x/0.01 = 1000W

Per soddisfare il rapporto a / b che abbiamo ottenuto, poniamo a e b più grandi possibili, in modo tale da rendere trascurabile l'effetto delle resistenze di contatto:

a = 100 W b = 10000 W

Verifichiamo dunque gli effetti della scelta dei parametri sulla sensibilità.

L'equivalente di Thevenin ai capi del galvanometro è:

La sensibilità è tanto migliore quanto più la tensione ai capi del galvanometro tende a E_o, e questo si verifica se R_i è piccola rispetto a g. Per cui valutiamo R_i , conosciamo g e dunque possiamo avere una stima dell'effetto della configurazione scelta sulla sensibilità.

R_i = (a // b) + (c // x) = (100 // 10000) + (1000 // 10) 100 + 10 = 110 W

g 10000 W dunque circa 1% della E_o cade su R_i il che implica una buona sensibilità.

Per quanto riguarda la risoluzione, se imponessimo c = 10000 W , sicuramente aumenterebbe ma ne conseguirebbe:

x / c = 0.001 = a / b,  con a = 10 W e b = 10000 W ; un valore di a così piccolo implica che bisogna tener conto anche delle resistenze di contatto, ma si preferisce non avere contributi significativi delle resistenze di contatto data la loro natura aleatoria.

Per queste ragioni scegliamo   a = 100 W b = 10000 W c = 1000 W

Per quanto riguarda il valore di E, all'equilibrio si ha:

P_x = x I₁² E =

P_c = c I₁² E =

P_a = a I₂² E =

P_b = b I₂²     E =

Affinché x non bruci è necessario che non assorba una potenza superiore ai 5 W; pertanto ponendo P_x = 0.5 W siamo sicuramente al riparo da rischi di questo tipo ed inoltre siamo certi che la sovra temperatura è accettabile ai fini della variazione di resistenza dovuta all'autoriscaldamento. In tali condizioni si ottiene:  E226 V

I valori di a, b, e c sono garantiti dal costruttore per potenze inferiori a 2 W.

Ponendo P_a = P_b = P_c = 2W   si ottengono i seguenti risultati:

a)      P_a = 2W   E = 1428 V

b)     P_b = 2W   E = 143 V

c)      P_c = 2W   E = 45 V

Dunque il valore massimo che può assumere la tensione E è pari a 45 V: partiremo da un valore di E pari a 25 V circa e se avremo bisogno di maggiore sensibilità la aumenteremo fino ad un massimo possibile di 35 V , che è il massimo consentito dal nostro alimentatore.

I ragionamenti fin qui svolti valgono anche per le altre misurazioni. In modo specifico per questo caso vanno considerate anche le resistenze di contatto come influenti sul valore di x, in quanto x=10 W con accuratezza al ^o/_oo comporta un'incertezza dell'ordine dei mW e le resistenze di contatto sono dell'ordine delle decine di mW. Il modo migliore di rendere trascurabile l'effetto delle resistenze di contatto è quello di metterle in serie a grandi resistenze: a questo scopo si usano resistori a 4 morsetti , collegati come mostra lo schema seguente

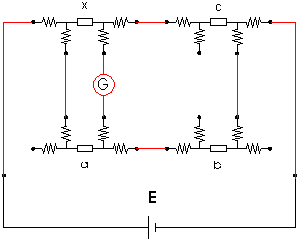
Si osservi che è possibile collegare solamente un resistore a 4 morsetti, gli altri sono a 2 o a 3 morsetti.

Materialmente, il resistore a 4 morsetti si realizza utilizzando 2 connessioni boccola-banana e 2 forchetta-banana.

2) x_n = 10 kW

Procedendo secondo i passaggi logici esposti per il caso 1) otteniamo:

dobbiamo poter agire sugli ohm di x, quindi

di conseguenza

perdiamo circa il 20% su Ri , il risultato è accettabile.

Eseguendo la prova ci si rende conto che la risoluzione non è sufficiente , quindi è necessario andare ad agire sui decimi di ohm di x.

Ne consegue che

Si perde il 50% su Ri , che è tanto.

Ma per rendere l'effetto delle resistenza di contatto trascurabile si può anche porre a=1kW e b=1kW, così

Si perde il 35% su Ri, che è un valore accettabile e garantisce la risoluzione desiderata.

3) x_n = 100 W

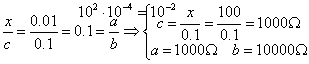
su Ri si perde il 10%.

Anche in questo caso eseguendo la misura ci si rende conto che occorre migliorare la risoluzione:

si deve poter agire sui milliohm di x.

Da cui

Perdiamo il 2% della tensione su Ri, siamo nella condizione ottimale.

DIARIO

STIMA DELLE INCERTEZZE

Le cause di incertezza sono: - il modello utilizzato

la sensibilità del ponte

le resistenze di contatto

le resistenze di dispersione

l'effetto Seebeck

- Per quanto riguarda l'effetto Seebeck, sia x₁ la resistenza misurata prima dell'inversione dell'alimentazione ed x₂ quella misurata dopo; avremo che:

x₁ = x + Dx'    x₂ = x - Dx'

dove Dx' è la variazione del valore della resistenza dovuta all'effetto Seebeck.

Quindi:

ovvero , facendo la media fra i due valori di x si elimina l'incertezza dovuta all'effetto Seebeck.

- Le resistenze di dispersione sono dell'ordine di un centinaio di MW. La resistenza più grande che usiamo è pari a 10 kW: il parallelo tra le due vale 10 kW // 100 MW 10 kW, ed è quindi lecito trascurare gli effetti delle resistenze di dispersione.

Per le resistenze di contatto si utilizzano gli accorgimenti già discussi in precedenza che consentono di trascurarne l'effetto.

Per l'incertezza dovuta al modello utilizzato e quella legata alla sensibilità del ponte, possiamo dire:

x =    quindi:

Tenendo conto anche della sensibilità del ponte:  

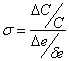
dove

e la si ricava sperimentalmente durante la misura:

dalla posizione in cui si trova durante la lettura si fa variare C di 0.1W (C=valore di C quando V_G DC=0.1W) e si legge di quante tacche si sposta l'indice del galvanometro (De=numero di tacche di cui si è spostato il galvanometro dalla posizione di equilibrio, de=1tacca)

RISULTATI OTTENUTI

X_n= 10 W

Stima dell'incertezza:

- e_a e_b

sperimentalmente abbiamo ottenuto s% = 0.005 %

Alimentazione diretta

lettura ( C ) W fatta a 0 tacche

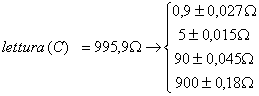    da cui C = 995,9 W

Inversione di alimentazione

lettura ( C ) W fatta a -1 tacche

C = 995,9 W

lettura ( C ) W fatta a +1 tacche

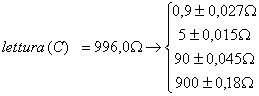    da cui C = 996,0 W

Per determinare il valore 757i87h di C con alimentazione invertita dobbiamo procedere per interpolazione tra i due valori ottenuti:

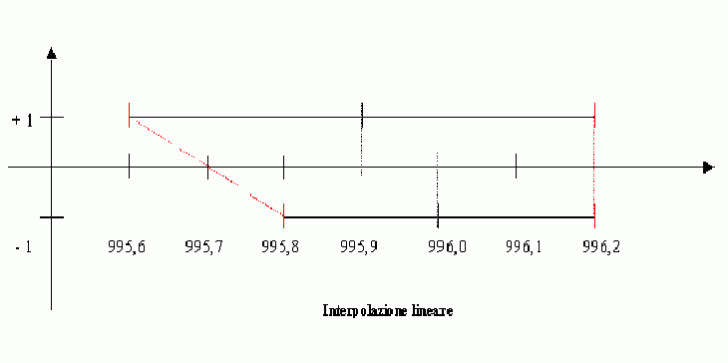
Da cui   C = 995,95 W

N.B. : L'interpolazione consente di guadagnare una cifra sola

In definitiva

C = [C(alimentazione diretta)+C(alimentazione inversa)]/2

In una somma le incertezze assolute si sommano , dunque

DC = DC (alimentazione diretta ) + DC (alimentazione inversa )

Eseguendo questi calcoli otteniamo:

C = ( 995,9 + 995,9 ) / 2 = 995,9 W

DC = 0,3 + 0,2 = 0,5 W

e_c

Ne risulta una incertezza complessiva pari a

e_x

La s non compare perchè dà un contributo che è dell'ordine dell'incertezza delle incertezze di e_{a ,}e_b, e_c

X_n= 10 KW

Stima dell'incertezza:

- e_a e_b

s% = 0.0003 % ( calcolata durante l'esecuzione della misura )

Alimentazione diretta

lettura ( C ) W

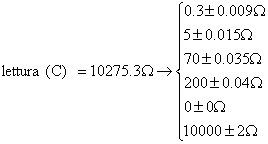    da cui C = 10275.3 W

Per determinare il valore 757i87h di C con alimentazione diretta dobbiamo procedere per interpolazione tra i due valori ottenuti:

10273.2 10277.4  fatta a +1 tacche

10273.1 10277.3  fatta a -2 tacche

da cui si ottiene

C = 10275.27 2.10 

Inversione di alimentazione

lettura ( C ) W

    da cui C = 10275.2 W

Per determinare il valore 757i87h di C con alimentazione invertita dobbiamo procedere per interpolazione tra i due valori ottenuti:

10273.1 10277.3  fatta a +1 tacche

10273.2 10277.4  fatta a -3 tacche

da cui si ottiene

C = 10275.22 2.10 

In definitiva

C = [C(alimentazione diretta)+C(alimentazione inversa)]/2

DC = DC (alimentazione diretta ) + DC (alimentazione inversa )

C = ( 10275,27 + 10275,22 ) / 2 = 10275,24 W

DC = 2,1 + 2,1 = 4,2 W

e_c

Ne risulta una incertezza complessiva pari a

e_x

La s non compare perchè dà un contributo che è dell'ordine dell'incertezza delle incertezze di e_{a ,}e_b, e_c

X_n= 100 W

Stima dell'incertezza:

- e_a e_b

s% = 0.003 % ( calcolata durante l'esecuzione della misura )

Alimentazione diretta

lettura ( C ) W fatta a 0 tacche

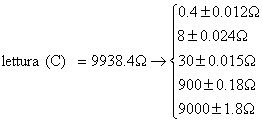    da cui C = 9938.4 W

Inversione di alimentazione

lettura ( C ) W fatta a 0 tacche

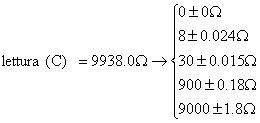    da cui C = 9938.0 W

In definitiva

C = [C(alimentazione diretta)+C(alimentazione inversa)]/2

DC = DC (alimentazione diretta ) + DC (alimentazione inversa )

C = ( 9938,4 + 9938,0 ) / 2 = 9938,2 W

DC = 2,031 + 2,019  4,0 W

e_c

Ne risulta una incertezza complessiva pari a

e_x

La s non compare perchè dà un contributo che è dell'ordine dell'incertezza delle incertezze di e_{a ,}e_b, e_c

RISULTATI FINALI

In definitiva abbiamo ottenuto i seguenti valori:

X_n = 10 W

X = * c = 0,01*995,9 = 9,959 W

DX = e_X * X ==0,009 W

quindi:  X = 9,959 0,009 W

X_n = 10 KW

X = * c = 1*10275,24 = 10275,24 W

DX = e_X * X ==8 W

quindi:  X = 10275 8 W

X_n = 100 W

X = * c = 0,01* 9938,2 = 99,382 W

DX = e_X * X ==0,08 W

quindi: X = 99,38 0,08 W

MISURE MEDIANTE OHMMETRI DI ALTA PRECISIONE

Lo scopo di questa seconda parte dell'esperienza è quello di avere dei risultati da poter confrontare con quelli ottenuti con il metodo del ponte di Wheatstone.

Apparecchiature usate

Multimetro digitale HEWLETT PACKARD E34401A:

Multimetro di precisione (in ambiente controllato):

Esecuzione della misura

Sono state effettuate le misurazioni dei resistori da 10 e da 10000 W con ohmmetri digitali aventi precisione diversa, ottenendo i seguenti risultati:

Stima dell'incertezza

È possibile stimare le cause d'incertezza, dovute unicamente allo strumento, grazie alla formula binomia che il costruttore riporta nel manuale:

errore totale = (errore lettura) (lettura) + (errore portata) (portata)

Si ottengono dunque i valori di R_x:

ANALISI DEI RISULTATI

Per ogni misura abbiamo ottenuto un'incertezza dell'ordine di 10^-4 raggiungendo così l'obiettivo prefissato.

Si osserva inoltre che :

x_n = 10 W 5%    x_n = 10 0.5 W

x_n = 10 kW 5%  x_n = 10 0.5 kW

x_n = 100 W 5%  x_n = 100 5 W

confrontando questi intervalli di valori con quelli ottenuti con il metodo del ponte di Wheatstone si vede che risultano compatibili.

Per confrontare i risultati ottenuti con il metodo a ponte con quelli delle misure con ohmetro occorre riportare le misure fatte ad una stessa temperatura , sfruttando la seguente formula:

dove Dt è il salto termico.

Xn=10 W

Metodo a ponte : temperatura ambiente = 25.1°C  x=9.959 W

Multimetro digitale : temperatura ambiente = 25.5°C   x=9.980 W

dunque x(25.1°C) = 9.979 W

Multimetro di precisione : temperatura ambiente = 22.9°C x=9.98055 W

dunque x(25.1°C) = 9.98494 W

Xn=10 kW

Metodo a ponte : temperatura ambiente = 25.3°C  x=10275 W

Multimetro digitale : temperatura ambiente = 25.5°C   x=10278.0 W

dunque x(25.3°C)=10277.6 W

Multimetro di precisione : temperatura ambiente = 22.9°C x=10277.868 W

dunque x(25.3°C)=10282.801 W

Né per x=10W né per x=10kW otteniamo la compatibilità delle tre misure. Ciò può essere imputabile al fatto che , per motivi di tempo, le due misure con ohmetro sono state fatte senza aspettare un tempo sufficiente affinché si raggiungesse l'equilibrio termico fra ambiente esterno e scatola contenente i resistori.