|
|
| |
Macchine termiche
Gli scambiatori di calore sono dispositivi in cui si realizza il trasferimento di un flusso termico tra due fluidi senza che si verifichi mescolamento tra i fluidi stessi.
Gli scambiatori di calore vengono classificati in base al percorso dei fluidi, come illustrato nelle figure.

Figura 7. - scambiatore contocorrente

Figura 7. 2 - scambiatore equicorrente
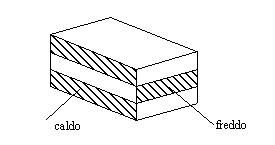
Figura 7. - scambiatore a flusso incrociato
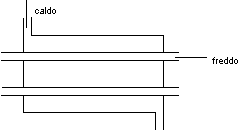
Figura 7. 4
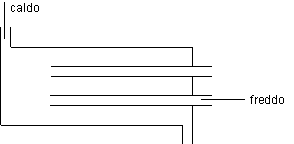
Figura 7. 5 - scambiatore a flusso tubiero a passaggi multipli
I principali fattori che caratterizzano le prestazioni di uno scambiatore di calore sono:
- lo scambio termico tra i fluidi;
- le perdite di pressione per attrito nei due circuiti.
Si definisce efficenza * di uno scambiatore il rapporto tra il flusso termico effettivamente scambiato tra i due fluidi e il flusso massimo teorico.
Il numeratore

Figura 7.
dove i vari pedici hanno il significato:
c = fluido caldo;
f = fluido freddo;
i = ingresso dello scambiatore;
o = uscita dello scambiatore.
Con riferimento alla figura 7.5 possiamo scrivere:
Qe
+ Li = ![]() (7.1)
(7.1)
Siccome non ci sono parti in movimento:Li = 0.
Inoltre siccome il sistema è isolato rispetto all'esterno: Qe = 0.
Infine si può considerare Eci 0 e allora la (7.1) può essere riscritta come:
mc ic + mf if = 0
mf if = -mcic
Se consideriamo solo il fluido caldo:
Qe + Li - mc( ic + Ec )= 0
che utilizzando le semplificazioni di prima si ottiene:
Qec = mc ic
Pertanto il numeratore
* = ![]()
dove (mcp)min rappresenta il minimo tra mfcpf e mccpc.
Qualitativamente, le prestazioni termiche di uno scambiatore di calore si possono caratterizzare in termini di thermal ratio :
c = ![]()
![]()
In generale l'efficenza si può esprimere come * = f(NTU, , percorso dei fluidi), dove:
NTU =![]() (NTU = Number of
Transfer Unit);
(NTU = Number of
Transfer Unit);
=![]() ;
;
H = coefficente globale di scambio termico tra i due fluidi;
A = superficie globale di scambio.
Un esempio tipico dell'efficenza dello scambiatore in funzione di NTU è riportato nella figura 7.6:
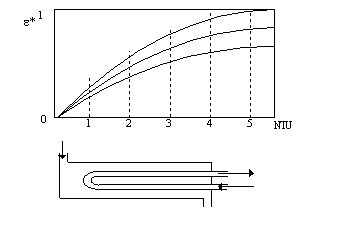
Figura 7. 7
E' bene che NTU sia sempre maggiore di 1, altrimenti risulta sottodimensionato, cioè HA è troppo piccolo rispetto a (mcp)min. Analogamente è bene che NTU non superi il valore 4, perchè in questo caso lo scambiatore risulterebbe sovradimensionato.
La distribuzione qualitativa della temperatura varia a seconda del tipo di scambiatore. In particolare si distingue tra equicorrente e controcorrente:
equicorrente

Figura 7. 8
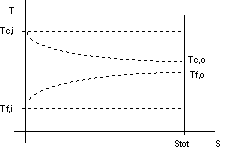
Figura 7. 9
I limiti di questo scambiatore sono:
- T decresce al crescere di S, quindi l'efficenza degli ultimi tratti è molto ridotta;
- Risulta: Tf,0 < Tc,o < Tc,i
Nel caso di vapore condensante (fluido caldo):
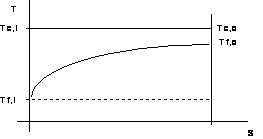
Figura 7. 10 - condensatori
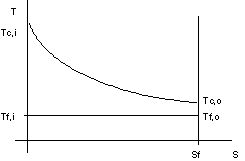
Figura 7. 11 - evaporizzazione
controcorrente
![]()
Figura 7. 12
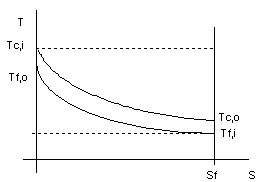
figura 7.11
Per questo tipo di condensatore si ha:
- T varia poco con S e pertanto l'efficenza dello scambiatore è quasi costante lungo S;
- Risulta: Tf,0 < Tc,i
quindi è meno restrittivo del caso precedente.
Nel caso del condensatore:
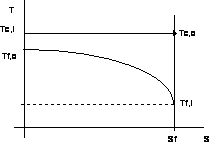
Figura 7. 13
La scelta tra scambiatore equicorrente o controcorrente è dettata da altre esigenze diverse dalla ottimizzazione della efficenza.
Nelle figure 7.13 e 7.14 sono rappresentati i tipi di scambiatori trattati.
[Vedere fogli a parte]
figura 7.13 - scambiatore a superficie
[Vedere fogli a parte]
figura 7.14 - scamiatore a miscela
Sono scambiatori di calore il cui scopo è la sottrazione di calore al vapore d'acqua, che costituisce il fluido di lavoro negli impianti termoelettrici per la produzione di energia elettrica.
La sottrazione del calore di condensazione al vapore può avvenire ad opera di un fluido ausiliario attraverso pareti metalliche (condensatori a superficie) oppure direttamente per mescolanza (condensatori a miscela).
Il fluido ausiliario di solito è acqua di fiume, di pozzo, ecc. negli impianti fissi; di mare negli impianti marini; mentre è più raro l'impiego dell'aria.
Nei condensatori a superficie occorre muovere il fluido ausiliario. Se il fluido è liquido si ottiene mediante pompe apposite dette pompe di circolazione; se il fluido è aeriforme si ottiene mediante ventilatori.
Negli impianti di turbine a vapore la condensazione ha i seguenti scopi, separati o congiunti:
Abbassamento della pressione finale di espulsione del vapore al di sotto della pressione atmosferica, e quindi aumento del salto di espansione (e del lavoro) che esso può sviluppare;
Recupero del calore posseduto dal vapore di scarico;
Recupero della condensa.
Il primo scopo presuppone che si abbia a disposizione un fluido ausiliario a temperatura inferiore di quella di saturazione del vapore corrispondente alla pressione atmosferica (100°C). Il condensatore è quindi relativamente freddo. Se invece lo scopo è il recupero del calore, la pressione e la temperatura di condensazione sono imposte dalle regioni dell'utilizzazione industriale, e sono di solito piuttosto elevate (condensatore caldo).
Il recupero delle condense interessa sia per non disperdere il calore del liquido che esso ancora possiede, sia perchè si tratta di acqua demineralizzata o addirittura distillata, utile e spesso necessaria per l'alimentazione della caldaia.
I condensatori a superficie che utilizzano acqua come fluido ausiliario sono costituiti da un cassone approssimativamente cilindrico o parallelepipedo, di solito ad asse orizzontale, contenente fasci di tubi percorsi internamente dall'acqua e lambiti esternamente dal vapore. I tubi sono assicurati alle piastre tubiere disposte sulle testate laterali del cassone.
Le testate costituiscono le camere di ingresso e di uscita dell'acqua condensatrice.
Il percorso dell'acqua condensatrice può essere semplice (da un estremo all'altro) o più volte ripiegato.
[Vedere fogli a parte]
figura 7.15 - condensatore a superficie
[Vedere fogli a parte]
figura 7.16 - condensatore a superficie
[Vedere fogli a parte]
figura 7.17 - condensatori a superficie
[Vedere fogli a parte]
figura 7.18 - percorso dell'acqua condensatrice per condensatori a superficie
[Vedere fogli a parte]
figura 7.19 - condensatore a miscela
L'acqua è introdotta direttamente nella camera di condensazione in modo tale da offrire la massima superficie di contatto al vapore con cui si mescola intimamente fino a produrre la condensazione. Ciò si ottiene o spruzzando l'acqua sotto pressione in modo da formare corone di getti finissimi che investano il vapore o, più comunemente, portandole nella parte alta della camicia e facendola poi traboccare dall'una all'altra di numerose bacinelle sovrapposte in modo da formare veli liquidi che il vapore è costretto ad attraversare.
Oltre all'inconveniente di non consentire il recupero della condensa, questo tipo di condensatore presenta, rispetto a quello a superficie, il difetto di maggiore quantità di aria da estrarre, poichè all'aria portata dal vapore si aggiunge quella disciolta nell'acqua condensatrice.
Il condensatore a miscela presenta viceversa il vantaggio di maggiore semplicità e di minor consumo di acqua condensatrice, essendo il salto Tv - Tu praticamente nullo.
Il calore trasmesso nell'unità di tempo dal vapore all'acqua condensatrice si può esprimere con la consueta formula degli scambiatori di calore:
Q = hS Tm
dove:
h è un coefficente globale di trasmissione del calore dal vapore all'acqua;
S è la superficie di scambio necessaria per la condensazione;
Tm è la differenza di temperatura media tra vapore ed acqua efficace ai fini di un bilancio termico globale.
La superficie di scambio è, di regola, la superficie totale dei tubi tra le pareti interne delle piastre tubiere.La differenza di temperatura media Tm presenta difficoltà in quanto essa dipende in maniera complessa dalla geometria del condensatore e dalla configurazione del percorso del vapore e dell'acqua.
Normalmente si utilizza per Tm la media logaritmica definita da:
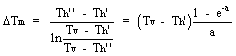
dove: Tv è la temperatura di saturazione del vapore all'ingresso del condensatore;
il coefficente a è defnito da:
![]()
L'espressione della media logaritmica esprime la differenza di temperatura media dedotta, con opportune semplificazioni, per uno scambiatore di calore a circolazione semplice, nell'ipotesi che la temperatura di uno dei due fluidi si mantenga costante, condizione questa approssimata in un condensatore.
Per quanta riguarda il coefficente globale h teniamo presente che la trasmissione di calore si opera dapprima per convezione dal vapore alla parete esterna dei tubi con un coefficente hv; poi dall'una all'altra parete dei tubi per conduzione con un coefficente K/s, essendo K la conducibilità termica del metallo di cui è fabbricato il tubo ed s è lo spessore; e finalmente dalla parete interna all'acqua con un coefficente di trasmissione per convezione hh.
In prima approssimazione si può utilizzare la seguente formula
che lega h a hv, ![]() e hh:
e hh: ![]()
dove: Se è la superficie esterna dei tubi;
Si è la superficie interna dei tubi;
Sm è la superficie media di scambio per conduzione definita da:
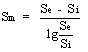
Nella prassi si utilizzano valori del coefficente globale di trasmissione h dedotti sperimentalmente per ciascun tipo di condensatore, cioè per qualsiasi tipo di geometria, percorso, ecc.
Sperimentalmente si è verificato che h soddisfa ad una relazione del tipo:
h
= cost. ![]()
dove w è la velocità dell'acqua nei tubi.
I valori medi di h sono compresi nell'intervallo h= 2500 4500 ![]() .
.
Ci limitiamo a considerare sistemi a due fluidi, uno scaldante e uno scaldato.
La generazione dell'energia termica avviene unicamente mediante combustione.

figura 7.20
ma = portata comburente;
mb = portata combustibile;
B = bruciatore (generatore di fiamma) il quale permette al combustibile e all'aria di reagire dando origine a una fiamma.
Nel bruciatore si ha una reazione chimica esotermica che mette a disposizione energia termica: nel principio di conservazione dell'energia occorre considerare il dEchimico.
Abbiamo il moto di un fluido attraverso un certo sistema e quindi sono presenti resistenze al moto (nelle prime applicazioni si collegava il tutto al camino che con la sua azione aspirante vinceva la resistenza al moto).
All'interno del generatore di calore si può individuare una zona (focolaio) in cui termina la combustione, a cui segue una zona di scambio termico, con diminuzione di volume massico.
Qe + Li = i* + Ec
dove:
i* = i + Uchim
applicata al fluido scaldante:
Qe = i* = if* - ii*
dove: i* = ![]() (7.2)
(7.2)
Hip = potere calorifico inferiore a pressione costante del combustibile;
cp'= capacità termica a pressione costante dei fumi;
= ![]() ed è denominata dosatura;
ed è denominata dosatura;
Tfc è la temperatura di fine scambio.
La relazione (7.2) vale per un tratto del bruciatore, prima dello scambio termico con il fluido scaldato.
Si distingue tra potere calorifico inferiore e superiore quando nei prodotti finali della combustione è presente H2O. Se l'acqua è presente sotto forma di liquido (Hs) o di vapore (Hi) abbiamo un diverso valore numerico dovuto al calore di condensazione dell'acqua presente.
Nei calcoli normalmente si considera Hi in quanto la temperatura dei fumi è tale per cui l'acqua presente è sotto forma di vapore.
I generatori di calore vengono distinti in :
caldaie acqua;
generatori di aria calda aria;
generatori di vapore vapore.
Le grandezze che caratterizzano il generatore di calore sono:
- potenza termica spesa: Ps = mbHi
dove: Hi = potere calorifico inferiore;
mb = portata di combustibile.
- potenza termica utile: Pu = m'(i'f - i'i)
La differenza tra Ps e Pu rappresenta le perdite, indicate come: Ps - Pu = Pi + Pd + Pe.
Pi = perdite per incombusti (vengono scaricati al camino gas in cui la reazione chimica non è finita, ad es. CO) fuligine presente: carbonio non completamente bruciato. Queste perdite dipendono dal bruciatore;
Pd = perdite per dispersione: pur essendo le pareti esterne sempre isolate (ad es. fibra di vetro,...) sono sempre presenti delle perdite;
Pc = perdite al camino: i gas combusti escono ad una temperatura superiore a quella ambiente: c'è una portata di fluido caldo che se ne va al camino ad una temperatura maggiore di quella con cui era entrata.
Definiamo rendimento del
generatore: ![]()
la scrittura corrisponde a fare il bilancio termico nel modo diretto, cioè misurando direttamente Pu e Ps e calcolando indirettamente:
![]()
Le perdite percentualmente più importanti sono Pc. Si può ritenere che valga:
![]()
dove:
A = costante che dipende dal tipo di combustibile ed eccesso di aria;
[CO2] legata a mb in base alla reazione chimica;
ta = temperatura ambiente.
tf''= temperatura finale dei gas combusti nel camino che essere alta per:
esigenze di tiraggio;
sicurezza (se è presente dello zolfo sa 140 °C si ha la temperatura di rugiada con la formazione di H2SO4).
Per legge il valore di tf'deve essere 180 350 °C.
Il valore di [CO2] deve essere alto in modo che, a parità di mb, m è inferiore, con portata complessiva di fumi al camino inferiore, e quindi minori perdite.
In alcuni casi occorre vapore d'acqua direttamente come utilizzare (es. industria acconciatura pellami); in altro casi si utilizza il vapore per la possibilità di fornire al fluido che evapora una grande entalpia, e quindi energia termica per unità di massa.

figura 7.21
Con valvola chiusa, fornendo energia termica la pressione sale.
Prelevando vapore attraverso la valvola, all'istante iniziale si ha la pressione voluta, ma successivamente diminuisce per la diminuzione di massa.
Introducendo una massa di liquido mediante una pompa (nella camicia è presente una pressione elevata) è possibile ottenere una portata di vapore a pressione costante.
La pressione all'interno del recipiente non è data dalla pompa, ma dall'energia termica ceduta dai fumi.
Il circuito scaldante è costituito da una serie di tubi dove si muovono i prodotti della combustione. Il fluido scaldato è contenuto dentro un involucro esterno, cilindrico all'interno del quale sono sistemati i tubi. Quindi i fumi scorrono dentro i tubi che vengono lambiti dall'acqua.
Il generatore di vapore (o caldaie) a tubi di fumo trova il suo tipico campo di impiego nelle modeste produzioni di vapore a bassa temperature.
Infatti la pressione non può essere elevata perchè con alte pressioni gli spessori del corpo cilindrico, del focolare e delle piastre tubiere assumono valori tali da non rendere la caldaia a tubi da fumo più competitiva.
In questi apparecchi il circuito scaldato è costituito da tubi che vengono detti tubi d'acqua (in genere c'è del vapore più liquido). Il vantaggio di questi generatori risiede nelle più contenute dimensioni di ingombro, con spessori ridotti e tensioni nel materiale accettabili pur con pressioni del liquido scaldato elevate. Quindi l'acqua scorre dentro i tubi i quali vengono scaldati dai fumi che li lambiscono.
La struttura del generatore è più complessa in quanto i tubi devono essere posti in modo da costituire il circuito scaldante. Dal punto di vista del circuito scaldato la circolazione dell'acqua si distingue in circolazione naturale e forzata e ad attraversamento forzato.
Si crea un moto dovuto alla differenza di densità tra fluido caldo e fluido freddo

figura 7.22
Vd: circuito discendente freddo;
Va: circuito acsendente; è scaldato e il suo stato, inizialmente corrispondente a Vd, passa alla curve limite superiore.
Aumentando la pressione diminuisce la differenza tra a e d, per cui con questo tipo di circolazione non è possibile realizzare cicli ipercritici.
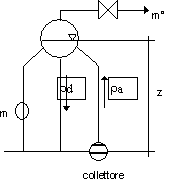
figura 7.23 - generatore di vapore a circolazione naturale
Con riferimento alla figura 7.23 definiamo la prevalenza motrice:
p = zg(d - a)
E' presente una pompa di circolazione che serve a creare un p supplementare per vincere le resistenze passive. Si chiama controllata perchè regolando le pompe si può controllare la circolazione.

figura 7.24
Si ha una portata circolante maggiore di m, che è da considerarsi un fattore di sicurezza sulla utilizzazione dell'energia termica.
Questo sistema funziona per differenza di densità, per cui è necessaria una differenza tra a e d.
In questo tipo di generatore scompare il corpo cilindrico il cui scopo era la separazione della zona di vaporizzazione dalla zona di surriscaldamento e la separazione dei sali presenti nell'acqua.
Questi apparecchi hanno una pompa di circolazione che in questo caso diventa anche causa del moto e pertanto servono a realizzare cicli ipercritici; c'è inoltre una maggiore libertà di disposizione dei tubi scaldati.
I generatori di vapore sono anche classificati in base alla trasmissione del calore:
- a convezione;
- a irraggiamento;
- a rimescolamento indiretto.
A stretto rigore di termini mentre esistono generatori che possono essere correttamente chiamati ad irraggiamento non si potrebbe parlare di generatori a convezione in quanto non esiste generatore nel quale una quantità più o meno grande di calore non sia trasmesso in caldaia per irraggiamento.
In camera di combustione il calore è trasmesso per solo irraggiamento; all'interno dei fasci tubieri vaporizzatori il calore è soprattutto trasmesso per convezione.

figura 7.25 - schema generatore di vapore ad irraggiamento
In figura 7.25 è rappresentato un generatore di vapore ad irraggiamento a sviluppo orizzontale a tubi d'acqua a circolazione naturale. I tubi ascendenti costituiscono l'involucro delle camere di combustione. Con analogo ctiterio sono schermate le altre pareti con i tubi.
Si definsce rendimento del generatore di vapore il rapporto tra la potenza termica ricevuta dal fluido nel generatore ed il prodotto della portata in massa di combustibile, mb, per il suo potere calorifico inferiore Hi:
![]()
e con riferimento al calore massico ![]() :
: 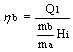
Questo rendimento tiene conto delle perdite per incompleta combustione; dispersione di calore attraverso le pareti della caldaia; calore disperso dai fumi.
Un fluido nell'attraversare un condotto o una turbomacchina evolve secondo le leggi della fluidodinamica. Esaminiamo ora il problema della determinazione della conformazione dei condotti e delle condizioni operative necessarie per ottenere che il fluido mentre scambia lavoro (ed eventualmente, calore) subisca determinate trasformazioni. Analogamente vogliamo individuare le trasformazioni che il fluido subisce nell'attraversare un condotto di forma assegnata e in determinate condizioni.
Supponiamo di voler far espandere un fluido comprimibile, inizialmente in quiete, dalle condizioni uniformi p1,v1,T1 fino a p2 < p1 e di voler disporre alla fine dell'espansione dell'energia cinetica conseguente alla diminuzione di pressione sotto forma di un getto con filetti fluidi paralleli e dotati della stessa velocità.
Supponiamo un flusso adiabatico e stazionario. La
trasformazione termodinamica che il fluido subisce dipende, oltre che dalla
natura del fluido, dalla legge con cui la sezione del condotto varia lungo
l'asse. La trasformazione può essere considerata reversibile (condotto breve,
superficie levigata) e il flusso unidimensionale. Definiamo la velocità del suono come la velocità con cui si propagano nel
fluido in quiete le piccole perturbazioni: 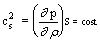
la derivata si intende calcolata lungo una linea ad
entropia costante (propagazione del fenomeno adiabatico reversibile, perchè si
hanno perturbazioni infinitesime). Per un gas perfetto, utilizzando l'equazione
pvk = cost., si ha: ![]()
ln p - k ln = cost.
![]()
![]()
![]()
Definiamo proprietà di ristagno (o totali o di arresto isoentropico) di una corrente fluida in modo permanente i valori che le proprietà della corrente acquisterebbero se questa fosse decelerata adiabaticamente e reversibilmente fino a velocità nulla senza scambiare lavoro.
L'entalpia di ristagno: i0
= i + ![]()
infatti da: Qe + Li = i + Ec
con Qe = Li = 0, indicando lo stato
iniziale con p,T,S,c e lo stato di ristagno con p0,T0,S0,
c = 0, si ottiene: i0 - i
- ![]() = 0
= 0
i0
= i + ![]()
per una trasformazione adiabatica (Qe = 0) che
avvenga tra gli stati stazionari 1 e 2 senza scambio di lavoro Li si
ha: ![]()
se il fluido soddisfa le proprietà di un gas perfetto si
ha: ![]()
dove: T0
= T + ![]()
la differenza di entropia fra gli stati stazionari 1 e 2
qualsiasi è uguale a quella dei corrispondenti stati di ristagno: S2 - S1 = ![]()
se il fluido soddisfa alle proprietà di un gas perfetto:
S2
- S1 = ![]() = cp ln
= cp ln![]() - R ln
- R ln ![]()
per un flusso adiabatico in un condotto fisso, essendo ![]() , si ha:
, si ha:
![]() = R ln
= R ln ![]()
si deduce quindi che in una trasformazione adiabatica e reversibile, in assenza di Li, la pressione totale è costante lungo il condotto.
Dall'equazione di continuità: m = Ac = cost.
Differenziando questa espressione e dividendo per Ac si ottiene:
![]()
Dall'equazione dell'energia: ![]() + i = cost (7.3)
+ i = cost (7.3)
scrivendo l'equazione nella forma: dQe + dLw = di - vdp
e considerando che dQe = dLw = 0, si
ottiene: di = vdp = ![]()
Differenziando la (7.3): c
dc + di = c dc +![]() = 0
= 0
da cui: c
dc = -![]() = -
= -![]()
![]() = -
= -![]()
![]()
e introducendo questo termine nell'equazione differenziale della continuità:
-![]() +
+ ![]() +
+ ![]() = 0
= 0
![]()
![]() +
+ ![]() = 0
= 0
e introducendo il numero di Mach Ma: Ma = ![]()
![]() =
= ![]()
![]()
sostituendo a ![]() l'espressione:
l'espressione: ![]() = -
= - ![]()
![]() = -
= -![]()
![]()
si ottiene: ![]() =
= ![]()
Queste espressioni valgono sia per un condotto accelerante, effusore o ugello, nel quale un fluido comprimibile subisce un'espansione con un aumento di velocità, sia per un condotto decelerante, diffusore, nel quale il fluido subisce una diminuzione di velocità e corrispondentemente un aumento di pressione.

figura 7.27
Per un fluido che si muove con velocità minore di quella del suono (c
< cs) si ha Ma < 1; per avere accelerazione (![]() > 0) segue che la sezione
deve diminuire:
> 0) segue che la sezione
deve diminuire: ![]() < 0
< 0 ![]() < 0
< 0
Una situazione opposta si
ha per per c > cs si
ha Ma > 1; per avere ![]() > 0 segue
che:
> 0 segue
che: ![]() > 0
> 0 ![]() < 0
< 0
Per c = cs si ha Ma = 1 e quindi: ![]() = 0
= 0
Per un fluido con velocità supersonica
(c > cs) si ha Ma > 1; per avere decelerazione e aumento della pressione (![]() < 0) segue che si deve ridurre la sezione (
< 0) segue che si deve ridurre la sezione (![]() < 0
< 0 ![]() > 0)
> 0)
Per c < cs si
ha Ma < 1; per avere![]() < 0 segue che:
< 0 segue che: ![]() > 0
> 0 ![]() > 0
> 0
Per c = cs si ha Ma = 1 e quindi ![]() = 0
= 0
La velocità c in una sezione generica del condotto vale (c1 = 0):
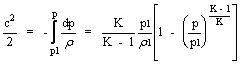 (7.4)
(7.4)
Questa relazionesi ottiene ricorando che la densità in una
sezione generica per espansione adiabatica reversibile vale 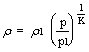 , la quale si ottiene dall'equazione di stato dei gas
perfetti.
, la quale si ottiene dall'equazione di stato dei gas
perfetti.
Dalla (7.4) si ricava:
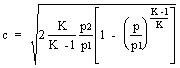
La sezione di condotto dovrà variare con la legge:
A
= ![]() A
A ![]()
e quindi:
c = 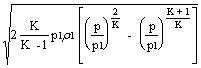
il massimo di c , corrispondente ad Amin, si ottiene derivando quest'ultima espressione rispetto a , trovando il rapporto critico delle pressioni:
![]()
al variare di K tra 1,135 e 1,67 si ha ![]() = 0,58 0,49.
= 0,58 0,49.
Se c1 non è trascurabile, valgono le
espressioni precedenti con le grandezze totali nella sezione 1. Ad esempio
nella (7.5) basta sostituire p1 con
![]() e 1 con
e 1 con ![]() .
.
Rappresentando questo termine in un diagramma cartesiano:
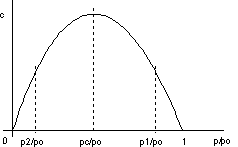
figura 7.29 - andamento del reciproco dell'area dell'ugello
Consideriamo la pressione pu nella sezione di efflusso Au coincidente con la pressione a valle p2 (ugello adattato). La portata vale:
m
= u Au cu
= Au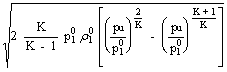
Supponiamo, per un dato ugello e un fluido di esponente K,
di far variare la pressione di valle p2 a parità di ![]() e
e ![]() .
.
Al diminuire di p2 la portata in massa aumenta fino
a raggiungere, per un valore di p2 pari a: p2 = pc = ![]()
un valore massimo in corrispondenza del quale nella sezione di efflusso si realizza la velocità critica:
cc
= csc = ![]() =
= ![]()
che dipende da K e dalle sole condizioni di monte.
Tale velocità, la corrispondente densità c e quindi m, resteranno invariate per valori di p2 minori di pc. Infatti per velocità di efflusso minori di cs le variazioni di pressione a valle dell'ugello possono risalire la vena fluida influenzando le condizioni. Se nella sezione di uscita si realizza la condizione critica, nessuna variazione della pressione a valle può attraversare tale sezione e di conseguenza far variare in essa la velocità, la densità e quindi la portata in massa.

figura 7.30
Per p pc:
m = Ac c cc = Au c cc = Au 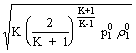
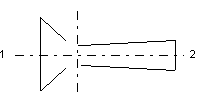
figura 7.31 - ugello convergente divergente
Rappresentiamo l'andamento della pressione lungo il condotto per un ugello progettato per lavorare tra le condizioni p1,c1 < cs e p2 = pa.
Facciamo quindi variare la pressione p2 a parità di condizioni del fluido a monte.

figura 7.32 - andamento della pressione lungo il condotto
Le condizioni di progetto sono:
- linea continua;
- la corrente è accelerata gradualmente fino a velocità supersonica all'uscita;
- ugello adattato.
Per p2 > pd il flusso è ovunque subsonico (curva b) il tratto convergente agisce da effusore; il tratto divergente funzione da diffusore: tubo di Venturi.
Per p2 = pd nella sezione ristretta la pressione raggiunge il valore critico, mentre la velocità raggiunge il valore sonico; nel tratto divergente si ha una diffusione della corrente in moto subsonico (curva d).
Per p2 < pd il flusso nella sezione ristretta, per un breve tratto, sarà supersonico seguito da una discontinuità nella pressione (urto retto o obliquo) nel tratto divergente o nella sezione di sbarco.
Per p2 < pa l'ulteriore espansione avviene a valle della sezione di sbocco con onde di espansione.
Da quanto detto si deduce che l'ugello De Laval è critico
per valori di ![]()
![]() , subcritico per
, subcritico per ![]() >
> ![]() (Tubo di Venturi).
(Tubo di Venturi).
L'andamento della portata è quindi:
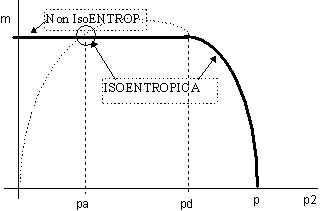
figura 7.21 - andamento della portata al variare di p2
Per l'ugello critico: m
= Ac 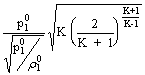
Nel caso di ugello critico adattato: m = Au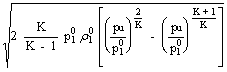
Uguagliando queste due espressioni si ottengono due valori
per ![]() dei quali quello
inferiore dà il valore di adattamento
dei quali quello
inferiore dà il valore di adattamento ![]() mentre quello
superiore corrisponde al valore discriminante
mentre quello
superiore corrisponde al valore discriminante ![]() .
.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025