La divisione di polinomi

Per trovare il quoziente Q(x) ed il resto R(x) della divisione, si segue questo procedimento:

si dispongono A(x) e B(x) ordinati secondo le potenze decrescenti di x:

si divide il primo termine 2x³ di A(x) per il primo termine x² di B(x), ottenendo il primo termine del quoziente Q(x):

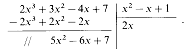
si moltiplica 2x per B(x) e si scrive il prodotto, cambiato di segno, sotto A(x), sommando in colonna i termini simili ottenendo A'(x):

4) si ripetono i passaggi 2) e 3) sostituendo A'(x) con A(x) finché A'(x) ha grado inferiore al grado del divisore.

A questo punto la divisione non può procedere oltre. A'(x) è il resto della divisione; il risultato è perciò il seguente:

Quoziente =    Q(x)= 2x + 5

Resto =   R(x)= -x + 2

Si usa nei casi in cui il polinomio divisore è un binomio di 1° grado, del tipo x k. Quando manca una potenza nel dividendo la si sostituisce con uno zero.

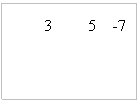Per trovare, ad esempio, il quoziente Q(x) ed il resto R della divisione si segue questo procedimento:

si dispongono nella 1a riga dello schema i coefficienti del dividendo, separando il termine noto;

si colloca in basso a sinistra il termine noto del divisore, cambiato di segno;

si abbassa il 1° coefficiente;

si moltiplica -3 per 3 e si pone il risultato in colonna;

si somma in colonna, ottenendo -4

si moltiplica -3 per -4, si pone il risultato in colonna e si somma, ottenendo 5;

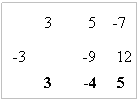L'aspetto finale dello schema è il seguente, in cui sono evidenziati i risultati della divisione;

Il quoziente Q(x) è sempre di un grado inferiore rispetto al dividendo: quindi il risultato della divisione è:

Q(x)= 3x -4    R= 5

Scomposizione con la regola di Ruffini

Esempio: x³+3x²-4.

Si considerano tutti i possibili divisori del termine noto -4; essi sono

Per tentativi si controlla se uno di essi, sostituito alla x nel polinomio, lo annulla:

sostituendo (-1) P(-1)=(-1)³+3(-1)²-4=-2

sostituendo (+1) P(+1)=(1)³+3(1)²-4=1+3-4=0

Poiché P(1)=0 il polinomio è divisibile per x -1: usando lo schema della divisione di Ruffini, si ottiene:

1 +3 0 -4

+1

Si esegue la divisione:

1 3 0 -4

+1 1 4 4

1 4 4

Per le note proprietà della divisione per cui a: b=q con 2 a= bq + 2,  la scomposizione è:

x³+3x²-4= (x-1)(x²+4x+4)

Teorema del resto

Nella divisione con Ruffini del tipo A(x): (x-a) il resto coincide con il valore numerico del dividendo calcolato per x= a cioè R= A(a).

Dimostrazione

A(x) : (x-a) = Q(x) e R(x) = R

A()= (x-a) Q(x) + r identità

sostituisco x = a

A(a)=(a-a) Q(a) + R

R=A(a)

Sono equazioni che contengono una sola incognita, che compare solo a primo grado: la loro forma normale è:  ax=b

Per quanto riguarda le costanti a e b, possono verificarsi questi tre casi:

a 0 e b qualsiasi (cioè b 0 oppure b=0)

L'equazione si dice determinata e la sua soluzione è .

a=0 e b

La forma normale è perciò 0x=b.

L'equazione si dice impossibile, perché non ha soluzioni: infatti ogni numero moltiplicato per 0 dà 0 (e non b).

a=0 e b=0

La forma normale è perciò 0x=0.

L'equazione si dice indeterminata, perché ha infinite soluzioni (è un'identità): infatti tutti i numeri moltiplicati per 0 danno 0.

Il procedimento per la risoluzione delle equazioni di 1° grado è il seguente:

si libera l'equazione dagli eventuali denominatori, facendo il m.c.d.;

si eliminano le parentesi, effettuando i calcoli;

si spostano i termini, in modo da avere al 1° membro solo quelli che contengono l'incognita;

si riducono i termini simili, portando l'equazione in forma normale;

si stabilisce se l'equazione è determinata (e si trova la soluzione), indeterminata o impossibile.

Sono equazioni in cui l'incognita compare anche a denominatore. Il procedimento di risoluzione prevede quindi il calcolo del minimo comun denominatore e la sua successiva eliminazione; è però necessario individuare prima quali valori dell'incognita rendono nulli i denominatori: infatti essi non possono essere soluzione dell'equazione, perché rendono priva di senso almeno una delle frazioni.

Esempio

La soluzione dell'equazione non potrà essere né 0 né ½, cioè dovrà essere diversa da questi due valori.

Due rette orientate fra loro perpendicolari si dicono assi cartesiani: essi dividono il piano in quattro quadranti.

Fissata un'unità di misura sugli assi, ad ogni punto P del piano corrispondono due numeri, ascissa e ordinata di P, che si dicono coordinate cartesiane ortogonali di P. Viceversa ad ogni coppia di numeri corrisponde uno ed un solo punto P del piano. L'origine degli assi viene chiamato solitamente punto O, e ha ascisse e ordinate nulle.

L'insieme di due equazioni di 1° grado in due incognite

si dice sistema di 1° grado in due incognite; soluzione del sistema è una coppia di numeri che sia soluzione contemporaneamente di entrambe le equazioni. Un sistema è ridotto in forma normale quando tutte le sue equazioni sono ridotte in forma normale. Due sistemi si dicono equivalenti quando ammettono le stesse soluzioni.

Un sistema di 1° grado può essere:

determinato, quando ammette una soluzione;

impossibile, quando non ammette soluzioni;

indeterminato, quando ammette infinite soluzioni.

Risoluzione dei sistemi di 1° grado con due equazioni a due incognite

Per un sistema ridotto in forma normale sono possibili quattro metodi di risoluzione e solo l'esame dei coefficienti delle due equazioni del sistema può, di volta in volta, indicare il metodo più opportuno.

Sostituzione

si risolve una delle equazioni rispetto a una delle incognite, ad esempio rispetto alla x;

si sostituisce l'espressione trovata nell'altra equazione e la si risolve,  trovando il valore della y;

si sostituisce il valore della y nell'espressione della x.

Confronto

si ricava la stessa incognita in entrambe le equazioni;

si uguagliano le due espressioni ottenute e si risolve, ottenendo il valore di una incognita;

si sostituisce il valore trovato in una delle equazioni iniziali, ottenendo il valore dell'altra incognita.

Cramer

Dati 4 numeri a, b, c, d il simbolo

rappresenta una matrice quadrata del 2° ordine.

Si chiama determinante della matrice, e si indica con il simbolo

il numero che si ottiene moltiplicando in croce e sottraendo i risultati;

Il metodo di Cramer per risolvere i sistemi si basa sul calcolo di tre determinanti, i cui elementi sono i coefficienti delle incognite x e y ed i termini noti del sistema.

Procedimento:

dato il  sistema in forma normale

si calcolano i tre determinanti

e la soluzione del sistema è:

x = Dx/D  y = Dy/D

Si pone una sola incognita x: tutte le altre quantità, di cui non si conoscono i valori, devono essere espresse mediante x. In questo modo il problema si risolve con un'equazione.

In alcuni problemi è comodo impostare il ragionamento con due incognite x e y: in questi casi, per la risoluzione, è però necessario avere due relazioni che legano le incognite fra loro o con i dati del problema.

In questo modo il problema si risolve con un sistema di due equazioni.

Una disequazione è in generale una disuguaglianza fra due espressioni letterali, verificata solo da particolari valori attribuiti alle lettere, che si dicono soluzioni della disequazione; tutte le soluzioni costituiscono l'insieme delle soluzioni della disequazione.  Risolvere una disequazione significa trovare l'insieme delle sue soluzioni.

Per le disequazioni vale il seguente principio di e1quivcalenza: aggiungendo uno stesso polinomio ai due membri di una disequazione, si ottiene una disequazione equivalente.

Le proprietà delle disequazioni:

si possono spostare i termini da un membro all'altro, purché si cambi loro il segno;

si possono moltiplicare o dividere i due membri per uno stesso fattore numerico, purché positivo;

si può cambiare il segno a tutta la disequazione, purché si cambi anche il suo verso;

si possono eliminare i denominatori, facendo prima il m.c.d. nei due membri;

Disequazioni intere di 1° grado

Sono disequazioni nelle quali l'incognita è presente a 1° grado. Il procedimento di risoluzione è il seguente:

si libera la disequazione degli eventuali denominatori;

si eliminano le eventuali parentesi, effettuando i calcoli;

si spostano i termini in modo da avere al 1° membro solo quelli che contengono la x;

si riducono i termini simili, portando in forma normale;

si fa in modo che il coefficiente della x sia positivo, cambiando segno, se necessario, a tutta la disequazione (e quindi anche il verso);

si trova x, risolvendo come nelle equazioni.

Disequazioni fratte

Sono le disequazioni del tipo

Il procedimento di risoluzione consiste nel risolvere due sistemi di disequazioni. Dato che esso è molto lungo e complesso, è più comodo utilizzare un metodo veloce e schematico per la risoluzione delle disequazioni fratte, basato sullo studio del segno del numeratore e del denominatore e l'applicazione della regola dei segni della divisione.

Si studia il segno del numeratore e del denominatore ponendoli entrambi >0, indipendentemente dal verso della disequazione;

Si rappresentano graficamente i segni del N e del D e, nei singoli intervalli, si ricava il segno del quoziente con la regola dei segni della divisione;

Si osserva quale segno dev'essere il quoziente, basandosi sul verso, minore = negativo, maggiore = positivo, e in base a quello si determinano le soluzioni della disequazione.

Disequazioni di grado superiore al secondo

Le disequazioni di grado superiore al secondo, la cui forma normale è

con n > 2

possono essere risolte se si riesce a scomporre il polinomio Pⁿ (x) in fattori di primo o di secondo grado.

Esempio pratico

Si scompone il polinomio in due fattori:

Si studia il segno dei due fattori, ponendoli entrambi > 0, indipendentemente dal verso della disequazione:

1° fattore > 0 x > 0

2° fattore > 0 x²-3x+2>0   x? risultato x<1 e x>2

Si rappresentano graficamente i segni dei due fattori e si ricava il segno del loro prodotto nei singoli intervalli mediante la regola dei segni della moltiplicazione:

0 1 2

1° fattore > 0   - + + +

2° fattore > 0  + + - +

Segno del - + - +

prodotto 

La disequazione chiede quando il prodotto è positivo (>0), per cui le soluzioni sono: 0 < x < 1 e x > 2.

Sistemi di disequazioni

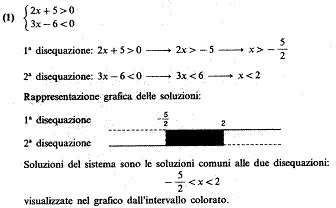
Un sistema di disequazioni è l'insieme di due o più disequazioni nella stessa incognita, che devono essere simultaneamente soddisfatte. Il procedimento di risoluzione consiste nel risolvere separatamente le singole disequazioni e determinare poi le soluzioni comuni.

Esempio

(sulla pagina seguente)

Dato un numero a reale positivo e un numero n naturale non nullo, si dice radice n-esima di a il numero che, elevato a n, dà per risultato a:

perché kⁿ=a

Il simbolo è detto radicale aritmetico:

n si dice indici del radicale

a si dice radicando

L'estrazione di radice è perciò operazione inversa dell'elevamento a potenza.

Proprietà invariantiva dei radicali

Il valore di un radicale non cambia se si moltiplicano il suo indice e l'esponente del suo radicando per uno stesso numero naturale non nullo.

Semplificazione dei radicali

Dalla proprietà invariantiva segue che un radicale non si altera se si dividono il suo indice e l'esponente del suo radicando per uno stesso numero intero positivo.

Un'operazione del genere si dice semplificazione del radicale.

Si può ottenere la forma più semplice di un radicale dividendo indice ed esponente del radicando per il loro m.c.d.: così il radicale diventa irriducibile.

Riduzione dei radicali allo stesso indice

Se si vuole che due o più radicali abbiano lo stesso indice, occorre ridurli al minimo comune indice, che è il m.c.m. dei loro indici.

Addizione e sottrazione di radicali

Si possono addizionare e sottrarre solo i radicali simili, cioè i radicali che hanno lo stesso indice e lo stesso radicando, come ad esempio:

La somma algebrica di radicali simili è un radicale a essi simile, che ha per coefficiente la somma algebrica dei coefficienti.

Moltiplicazione di radicali

Se i radicali hanno lo stesso indice, il prodotto è un radicale che ha ancora lo stesso indice e per radicando il prodotto dei radicandi.

Se i radicali hanno indici diversi, occorre ridurli allo stesso indice, prima di effettuare la moltiplicazione.

Divisione di radicali

Se i due radicali hanno lo stesso indice, il quoziente è un radicale che ha ancora lo stesso indice e per radicando il quoziente dei radicandi.

Se i due radicali hanno indici diversi, occorre ridurli allo stesso indice, prima di effettuare la divisione.

Potenza di un radicale

Per elevare a potenza un radicale si eleva a potenza il suo radicando:

Radice di un radicale

La radice di un radicale è un radicale  che ha per indice il prodotto degli indici:

Trasporto di un fattore sotto radice

Un fattore positivo può essere portato sotto radice (a fattore del radicando), purché lo si elevi all'indice della radice.

Radicali doppi

Sono espressioni del tipo

Si può tentare di trasformarle nella somma algebrica di radicali semplici, mediante la formula:

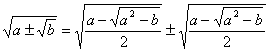
Razionalizzazione del denominatore delle frazioni

Quando una frazione ha dei radicali al denominatore, conviene razionalizzarla, trasformarla cioè in una frazione equivalente che non ha radicali al denominatore. Il metodo che si segue per razionalizzare il denominatore di una frazione è quello di moltiplicare opportunamente per uno stesso fattore il numeratore e il denominatore (proprietà invariantiva delle frazioni).

Esaminiamo i casi più frequenti di razionalizzazione.

1° caso:

la frazione è del tipo

cioè ha una radice quadratala denominatore

Per razionalizzare basta moltiplicare numeratore e denominatore per

2° caso:

la frazione è del tipo

cioè ha un radicale qualsiasi al denominatore.

Per razionalizzare basta moltiplicare numeratore e denominatore per

3° caso:

la frazione è del tipo

cioè ha la somma di due radici quadrate al denominatore.

Per razionalizzare si moltiplicano numeratore e denominatore per la differenza , realizzando il prodotto notevole

4° caso:

la frazione è del tipo

cioè ha la differenza di due radici quadrate al denominatore.

Per razionalizzare si moltiplicano numeratore e denominatore per la somma

5° caso:

la frazione è del tipo

cioè ha la somma o la differenza di due radici cubiche al denominatore.

Per razionalizzare si moltiplicano numeratore e denominatore per per realizzare il prodotto notevole [.]

Potenze a esponente frazionario

La potenza di un numero a reale e positivo, con esponente frazionario positivo , è uguale al radicale che ha per indice il denominatore n e per radicando a^m:

Ogni equazione che, ridotta in forma normale, si può scrivere nella forma

con a 0 e a,b,c R

si dice equazione di 2° grado.

Se sono presenti tutti i tre termini, l'equazione si dice completa. Se manca il temrine di 1° grado (b=0), l'equazione si dice pura; se manca il termine noto (c=0), l'equazione si dice spuria.

Se mancano contemporaneamente il termine di 1° grado e i termine noto (b=0 e c=0), l'equazione si riduce alla forma ax²=0, la cui soluzione è x=0 (radice doppia). Risolvere un'equazione di 2° grado significa trovare le sue soluzioni o radici, cioè i valori che, sostituiti alla incognita, verificano l'equazione.

Nella risoluzione delle equazioni di 1° grado complete e incomplete è spesso usata la legge di annullamento del prodotto: essa afferma che il prodotto di due fattori è nullo se:

  a=0

b=0