 |  | |
|
| | |
|
| |
CORSO: Statistica
LIBRI: Statistica per le decisioni + testi di autovalutazione
Supponiamo di aver rilevato dei dati. - Esiste una popolazione (o collettivo, o universo)
Ciascun punto rap 848d37i presenta un'unità statistica
Su ciascuna di queste unità vengono osservati uno o più caratteri
Continui Discreti QUANTITATIVI
Caratteri
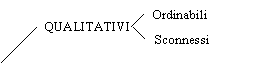
L'elenco di tutti i possibili valori assumibili da un carattere prende il nome di "modalità"
Se dato un elenco di modalità, esiste un ordine, siamo in presenza di qualitativi ordinabili se no disconnessi; se esiste la possibilità e il senso di calcolare la "distanza" tra un carattere e l'altro, siamo in presenza di quantitativi discreti.
|
OPERAZIONI |
QUALITATIVI |
QUANTITATIVI |
|
|
Ordinabili |
Sconnessi |
||
|
|
X |
X |
X |
|
>< |
X |
|
X |
|
+ - x : |
|
|
X |
Esercizio di esempio: Abbiamo un elenco rilevato di dati sul sesso di alcuni individui; calcolare la media
|
Individuo |
Sex |
|
1 |
|
Dove 0=femmina e 1=maschio
ATTENZIONE!!! In questo esercizio non si può calcolare la media, perché appunto non ha senso fare la media del sesso!!!
DEFINIZIONI:
Frequenza: Numero di volte che viene osservata una
certa modalità
Distribuzione di Frequenza assoluta: Elenco di modalità con le relative frequenze assolute
Distribuzione di Frequenza relativa: Rapporto tra ciascuna frequenza assoluta e il totale delle osservazioni
|
|
n |
fi |
Ni |
Fi |
|
A |
na |
fa= na/N |
na |
fa |
|
B |
nb |
fb |
na+ nb |
fa+ fb |
|
C |
nc |
fc |
nb+ nc |
fb+ fc |
|
D |
nd |
fd |
N |
|
|
|
N |
I |
|
|
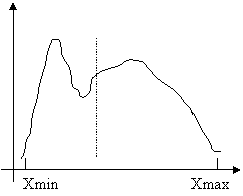Ci chiediamo la posizione dell'indice lungo l'asse X, per certo
sappiamo che deve comunque stare tra Xmin e Xmax.
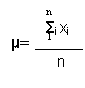
La formula significa: somma dei dati rilevati fratto numero di dati rilevati.
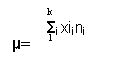
k
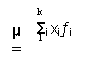
- Formula di media nel caso di distribuzioni di frequenze relative -
Esercizio di esempi: Quale è il reddito medio di questa popolazione di persone?
|
R |
n |
|
|
|
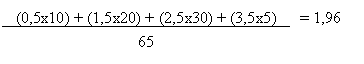
Supponiamo che R passi ad R+1 - Per calcolare il risultato occorre solamente sommare 1 alla precedente formula senza dover ricalcolare il tutto!
Supponiamo di dover convertire il reddito dato in milioni di lire in euro - Anche qui per calcolare il risultato vado ad agire sulla formula, dividendo il suo risultato finale.
- SCARTI DELLA MEDIA ARITMETICA - (xi - μx)
La sommatoria di tutti gli scarti è = 0
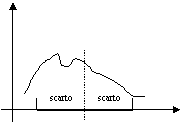Nessun valore all'interno della distribuzione ha una somma del quadrato
degli scarti più basso della media aritmetica. Bisogna trovare il punto meno
distante da tutti gli altri.
XK X2 X1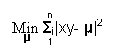
Minimizzazione della somma dei segmenti che sottengono tra dato osservato e indice di posizione.
L'indice di posizione media rappresenta bene i dati ricavati?
E' necessario affiancare alla media un atro indice che ci dice quanto la distribuzione di frequenze è vicina o lontana dall'indice di posizione (quanto sono lunghi i segmenti): La "varianza" (o quadrato dello scarto quadratico medio) che vale a dire lo scarto quadratico medio della media aritmetica:
|
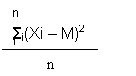
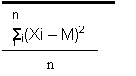
Lo scarto quadratico medio invece è la radice quadrata della varianza:
- IL NUMERO INDICE E GLI INDICI -
Il numero indice rappresenta la variazione di un qualcosa; è rappresentato dal rapporto di un fenomeno fratto se stesso ma in due periodi diversi.
Il numero indice non è una forma di media! Al più è il rapporto tra 2 medie.
Ad esempio se si ipotizzasse il rapporto tra i prezzi del 2005 con quelli del 2004 bisognerebbe moltiplicare i due prezzi (cioè quello 2005 al numeratore e quello 2004 al denominatore) per le quantità.
Sulla base dell'indice dei prezzi, vengono ricontrattati i contratti di lavoro, gli affitti etc.
Problema. E se la media dovesse essere calcolata su un carattere non quantitativo? Cosa si fa?
Ad esempio i ragazzi italiani sono tenuti a rispondere su quale tipo di ragazze tra castane, bionde e more, piacciono di più. Non si può far la media in questo caso, perciò si ricorre al calcolo della MODA, ovvero il carattere che più frequentemente è stato scelto.
La mediana non si può calcolare su caratteri qualitativi.
Si calcola però su carattere quantitativo, ipotizziamo la seguente tabella di dati raccolti:
|
|
|
fi |
Fi |
|
|
|
|
|
La mediana, come evidente dalla tabella è la classe 2
In
questo caso Me=
2 + 2 (0,5-0,2)/0,4 = 3,5
|
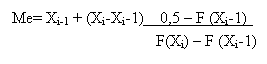
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025
