b)  si studi e si disegni G

c)  si determini, applicando uno dei metodi numerici studiati, un'approssimazione della intersezione positiva di G con l'asse x;

d)  si determini l'equazione della curva G' simmetrica di G rispetto alla retta y = y(1);

e)  si disegni, per i valori di a e b trovati, il grafico di:

RISOLUZIONE

a)  le informazioni di cui disponiamo sono:

la prima in quanto la funzione passa nell'origine, la seconda in quantox=1 è min.

sostituendo nella funzione e nella derivata che risulta essere:

otteniamo il seguente sistema:

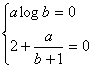da cui sostituendo e raggirando si ottiene:

b)  La funzione così riscritta risulta essere:

L'unica condizione è sull'esistenza del logaritmo: x>-1, quindi il dominio risulta esesre:

 Essendo D non simmetrico rispetto all'origine, è inutile cercare eventuali simmetrie. Ricerco le intersezioni con gli assi:

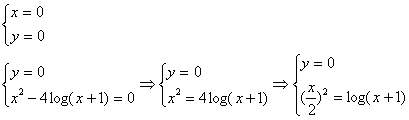
 si risolve per via grafica:

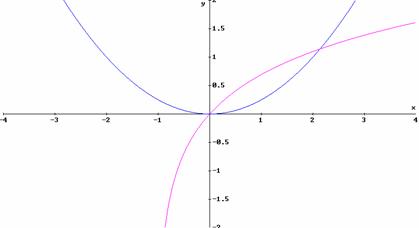
e si osserva che ci sono due soluzioni: , entrambe accettabili.

Limiti alla frontiera del dominio:

 da cui si deduce che in x=1 la funzione ha un asintoto verticale.

Raccogliamo e otteniamo: . Risolvendo la forma d'indecisione con il teorema di De L'Hopital nella frazione dentro la parentesi, si ottiene che la frazione tende a 0, quindi la parentesi va a 1, di conseguenza il limite iniziale tende tutto a .

In conseguenza di ciò, la f(x) non presenta asintoti orizzontali, quindi si va alla ricerca dell'eventuale asintoto obliquo:

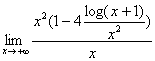che semplificando, risulta essere , quindi la f(x) non ha asintoto obliquo.

La prima soluzione è accettabile, la seconda no, in quanto non rientra nelle condizioni di dominio.

Il denominare, sotto condizioni di dominio è sempre positivo.

Lo schema della derivata prima risulta essere:

-1 1

XXX-------+++++++

m

che non si può mai annullare ed è sempre maggiore di 0. Di conseguenza f(x) ha sempre la concavità rivolta verso l'alto.

XXX+++++++

Il grafico risulta essere il seguente:

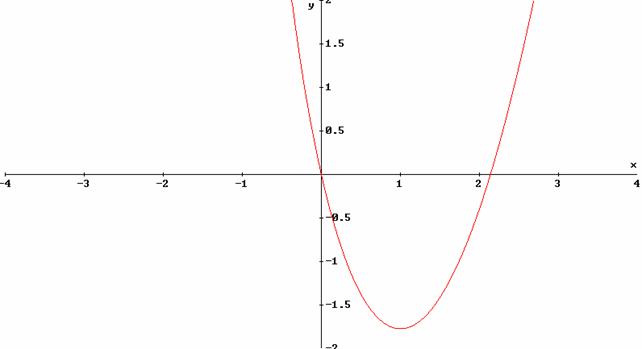
c) Determinare , ad esempio attraverso il metodo di bisezione:

Da cui si ottiene con approssimazione a  che

d)  Utilizzando la trasformazione di simmetria rispetto a una retta orizzontale si ha:

riaggirando e ricavando x e y si ottiene: e andando a sostituire nella funzione di partenza e sapendo che si ha che è :

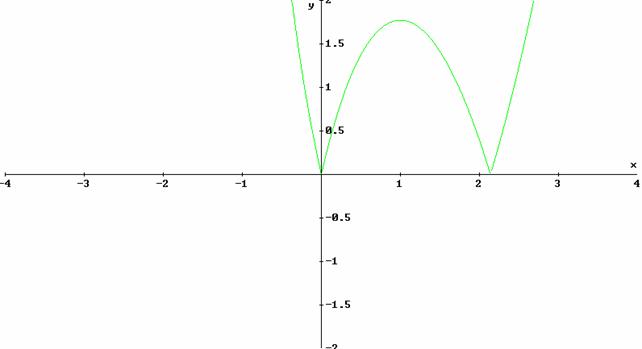
e)  per disegnare basta partire da e simmetrizzare rispetto all'asse x i tratti con y<0. Il grafico risulta: