|
|
| |
SISTEMI DI PRODUZIONI
La risoluzione di un problema può essere vista come ricerca nello spazio degli stati. Ad esempio, per costruire un programma che giochi a scacchi occorre specificare la configurazione di partenza della scacchiera, le regole che definiscono le mosse legali e quali posizioni sulla scacchiera rappresentano la vittoria per una delle due parti. Inoltre lo scopo non è solo quello di giocare una partita a scacchi, ma anche quella di vincerla possibilmente!
Risulta evidente che un normale programma inteso come sequen 515b12f za fissata di azioni, con un tipo di controllo predeterminato ed esplicito richiederebbe troppo tempo per fornirgli l'insieme completo di regole che governano il problema da risolvere. Senza contare i problemi derivati dalla memorizzazione della notevole quantità di informazione.
I sistemi di produzione sono sistemi di ragionamento automatico che usano le implicazioni come rappresentazione primaria per poter costruire programmi efficienti che ragionano con la logica. Il conseguente di ogni implicazione viene interpretato come suggerimento di azione, piuttosto che una semplice conclusione logica. Dunque i Sistemi di Produzioni descrivono le operazioni che portano alla soluzione di un problema definito su uno spazio di stati.
UnUnn xSono costituiti da:
una Base di Conoscenza o Memoria di Lavoro: il sistema di produzioni mantiene le informazioni sul problema sottoforma di letterali positivi senza variabili (secondo la logica del primo ordine). Tale memoria consiste del "data base", costituito dallo stato iniziale, stato obiettivo, parti permanenti, e parti rilevanti per la soluzione del problema;
un insieme di regole di inferenza: il sistema di produzioni mantiene delle regole atte a modificare lo stato del sistema, ognuna delle quali nella forma
![]()
dove Pi sono letterali, Azionei sono azioni da intraprendere quando i Pi sono tutti soddisfatti.
Tali regole sono mantenute in una memoria separata. Le azioni consentite sono l'aggiunta e la rimozione di elementi dalla memoria di lavoro ed eventualmente altre azioni (come la stampa di un valore).
una strategia di controllo: specifica l'ordine con cui le regole vengono scelte per evitare conflitti nel caso più regole possano essere applicate contemporaneamente, ed è anche un modo per facilitare la descrizione e l'esecuzione del processo di ricerca. Ad ogni ciclo il sistema calcola il sottoinsieme di regole il cui lato sinistro soddisfa i contenuti correnti nella memoria di lavoro. Questa è detta fase di accoppiamento. Il sistema quindi decide quale regole deve essere eseguita. Questa è detta fase di risoluzione di conflitti. Il passo finale di ogni ciclo consiste nell'esecuzione dell'azione (o azioni) della regola scelta, detta fase di azione.
un sistema per applicare le regole.
Per ora la definizione di un sistema di produzioni è ancora del tutto generale. Vedremo, in pratica, che la risoluzione di un problema consiste nel trovare un cammino da uno stato iniziale ad uno stato obiettivo, attraverso l'applicazione delle regole, mediante un'appropriata strategia di controllo per muoversi nello spazio degli stati (scelta delle regole da applicare).
Sono dati 2 secchi non graduati da 4 e 3 litri e una pompa per riempirli. Come è possibile mettere 2 litri d'acqua nel secchio da 4 litri?
Per la soluzione di devono definire:
Lo spazio degli stati coppie di valori (x,y) tali che x=0,1,2,3,4 ed y=0,1,2,3 indicano il numero di litri nei due secchi.
Lo stato iniziale o di partenza definito dalla coppia (0,0), per indicare che i due secchi sono inizialmente vuoti.
Lo stato obiettivo o il goal: (2,n) per un qualsiasi valore di n (poiché il problema non specifica quanti litri devono trovarsi nel secondo secchio).
Le regole: le azioni che portano ad un mutamento dello stato. E' necessario aggiungere delle regole non specificate dall'enunciato.
 La strategia di
controllo è la scelta della regola da applicare e
influenza la velocità di raggiungimento della soluzione. Una
regola è costituita da una parte sinistra, che determina l'applicabilità della
regola, e da una parte destra che descrive le operazioni da compiere se viene
applicata la regola. Per l'esempio in questione il sistema risulta essere il
seguente:
La strategia di
controllo è la scelta della regola da applicare e
influenza la velocità di raggiungimento della soluzione. Una
regola è costituita da una parte sinistra, che determina l'applicabilità della
regola, e da una parte destra che descrive le operazioni da compiere se viene
applicata la regola. Per l'esempio in questione il sistema risulta essere il
seguente:
|
Litri d'acqua nel secchio da 4 litri |
Litri d'acqua nel secchio da 3 litri |
Regola applicata |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 o 11 |
|
|
|
9 o 11 |
Per un aumento dell'efficienza del programma le condizioni devono essere soddisfatte prima che l'operatore venga applicato.
E' opportuno riconoscere le regole che descrivono il problema e le regole che, oltre a descrivere il problema, aggiungono della conoscenza per raggiungere la soluzione
![]() Le ultime due regole
formalizzano la possibilità di versare un quantitativo ignoto; è permesso dal
problema, ma probabilmente non porterà alla soluzione. Ora discuteremo il modo in cui si ottiene una possibile
soluzione come quella della Tabella 1.
Le ultime due regole
formalizzano la possibilità di versare un quantitativo ignoto; è permesso dal
problema, ma probabilmente non porterà alla soluzione. Ora discuteremo il modo in cui si ottiene una possibile
soluzione come quella della Tabella 1.
La questione di come decidere quale regola applicare durante il processo di ricerca della soluzione di un problema è ciò che viene definita Strategia di Controllo. Poiché i conflitti possono avvenire con una certa frequenza quando più di una regola ha la parte sinistra corrispondente allo stato attuale, il modo in cui avvengono le decisioni può influire sulla rapidità e finanche sulla possibilità di risolvere un problema.
Per una buona strategia di controllo occorre rispettare i due requisiti di bontà
possibilità di causare movimento: se nel problema dei secchi d'acqua si adottasse la semplice strategia di controllo che tutte le volte parte dall'inizio della lista delle regole e sceglie la prima applicabile, continueremmo all'infinito a riempire il secchio da 4 litri, dunque non risolveremmo mai il problema se non ci fosse movimento nella strategia adottata.
sistematicità supponiamo di scegliere a caso una delle regole applicabili ad ogni ciclo. Tale strategia causa movimento e alla fine ci condurrà ad una soluzione, ma durante il processo c'è la possibilità di andare più volte nello stesso stato influendo sulla rapidità.Questo perché non c'è una sistematicità nella strategia adottata.
E' utile pensare al processo di ricerca come la costruzione di un albero di ricerca i cui nodi sono stati e i cui rami sono operatori. Un programma dedito alla risoluzione di un problema potrebbe, ad esempio, applicare ogni operatore e ogni possibile combinazione di operatori alla formula data e a quelle derivate, generando ogni possibile variazione fino a trovare quella che corrisponde alla premessa.
In mancanza di una piantina o di una bussola, le regole euristiche possono venire in aiuto: di solito è possibile trovare il centro cittadino cercando la strada principale o centrale, o comunque procedendo in modo che la numerazione delle strade sia in ordine decrescente. Non è detto che questo consiglio porti sempre e comunque al centro, e tanto meno che indichi sempre il percorso migliore; comunque, questo metodo permette di limitare l'area di ricerca, e nella maggior parte dei casi porta alla destinazione desiderata.
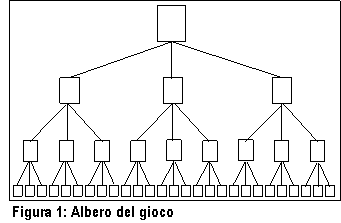 L'applicazione
della ricerca guidata dalle regole
euristiche è stata d'aiuto a molti giochi cosiddetti "intelligenti" come la
dama o gli scacchi. Un computer deve analizzare un labirinto di possibilità,
studiare le potenziali mosse una dopo l'altra, giudicando al tempo stesso la
possibile risposta dell'avversario, il modo migliore per controbatterla e così
di seguito. Per rappresentare questo procedimento si utilizza il cosiddetto
"albero del gioco". Alla radice dell'albero c'è un quadrato che rappresenta la
configurazione della scacchiera all'inizio della partita. Le possibili mosse
che il primo giocatore può effettuare sono rappresentate da linee che portano
ad una fila sottostante di quadrati, che a loro volta rappresentano l'aspetto che assumerebbe la
scacchiera se venisse effettivamente fatta quella particolare mossa. Anche in
una partita semplicissima, in cui si suppongano soltanto tre diramazioni a ogni
mossa, l'albero del gioco acquista ben presto un fitto fogliame (Fig. 1).
L'applicazione
della ricerca guidata dalle regole
euristiche è stata d'aiuto a molti giochi cosiddetti "intelligenti" come la
dama o gli scacchi. Un computer deve analizzare un labirinto di possibilità,
studiare le potenziali mosse una dopo l'altra, giudicando al tempo stesso la
possibile risposta dell'avversario, il modo migliore per controbatterla e così
di seguito. Per rappresentare questo procedimento si utilizza il cosiddetto
"albero del gioco". Alla radice dell'albero c'è un quadrato che rappresenta la
configurazione della scacchiera all'inizio della partita. Le possibili mosse
che il primo giocatore può effettuare sono rappresentate da linee che portano
ad una fila sottostante di quadrati, che a loro volta rappresentano l'aspetto che assumerebbe la
scacchiera se venisse effettivamente fatta quella particolare mossa. Anche in
una partita semplicissima, in cui si suppongano soltanto tre diramazioni a ogni
mossa, l'albero del gioco acquista ben presto un fitto fogliame (Fig. 1).
La ricerca è comunque il nucleo di molti processi "intelligenti". Un algoritmo di ricerca prende come input un problema e restituisce una soluzione nella forma di una sequenza di azioni.
Una volta trovata la soluzione, avviene la fase di esecuzione, in cui le operazioni e i passi trovati per raggiungere il goal vengono eseguiti.
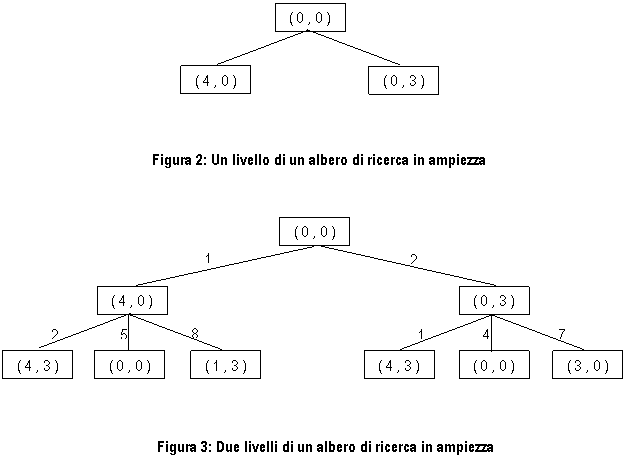 Per
l'esempio dei secchi d'acqua si può pensare alla costruzione di un albero la
cui radice sia lo stato iniziale e i figli della radice generati dalle regole
applicabili allo stato iniziale (fig. 2).
Per
l'esempio dei secchi d'acqua si può pensare alla costruzione di un albero la
cui radice sia lo stato iniziale e i figli della radice generati dalle regole
applicabili allo stato iniziale (fig. 2).
A questo punto, per ogni foglia si generano tutti i successori applicando tutte le regole opportune. L'albero diventa quello in fig. 3 dove sono state ignorate le regole 3, 4, 11, 12. Il processo continua fino a quando una qualche regola produce uno stato obiettivo. Tale ricerca viene definita in ampiezza, ed è una particolare strategia cieca in cui si cerca lo stato obiettivo esaminando "in orizzontale" tutte le possibilità dell'albero.
In seguito verranno esaminate diverse metodologie di ricerca. Per ora lo studio è concentrato sull'analisi dei sistemi di produzione.
L'utilizzo delle regole di produzione seguono diverse metodologie di ragionamento: Deduzione, Abduzione, Giustificazione. Prendiamo, ad esempio, la seguente regola:

Deduzione: Si assume il FATTO 1 noto a priori. Dall'applicazione della regola possiamo asserire che il FATTO 2 è vero
Abduzione: Si assume il FATTO 2 noto a priori. Dall'applicazione della regola possiamo dedurre che il FATTO 1 è vero.
Giustificazione: Assumiamo vero FATTO 1 e FATTO 2, dalla regola si deduce che si può trovare una plausibile giustificazione sullo stato dei due fatti.
Il ragionamento Deduttivo si ottiene attraverso il concatenamento in avanti o a priori (forward chaining) di una o più regole, detto anche data driver, cioè ragionamento guidato dai dati.
Quello abduttivo, invece, è definito dal concatenamento all'indietro o a posteriori di una o più regole, detto goal driver, o meglio ragionamento guidato dalla soluzione parziale trovata.
I Sistemi di produzione operano principalmente con una struttura di controllo a concatenazione in avanti. Alcuni hanno meccanismi di risoluzione dei conflitti per decidere quale azione intraprendere quando ne viene suggerita più di una. Esempi sono Ops-5, CLIPS, SOAR.
 Il
PROLOG e la maggior parte dei linguaggi di programmazione sono a concatenazione
all'indietro. Data un'interrogazione cercano una dimostrazione costruttiva che
stabilisca una qualche sostituzione che soddisfi l'interrogazione. Un esempio
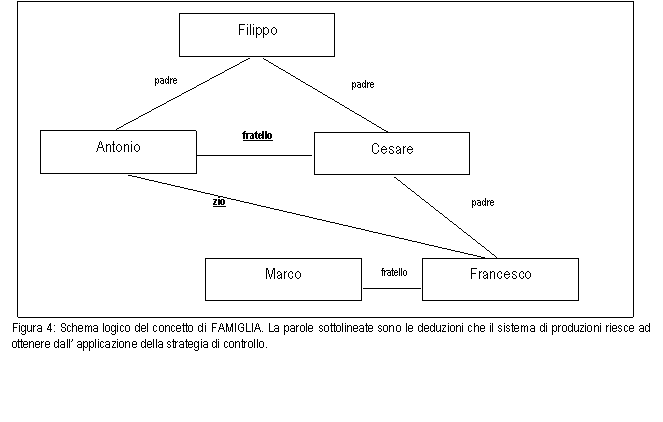
chiarirà meglio: supponiamo di voler dare delle regole sul concetto FAMIGLIA:
Il
PROLOG e la maggior parte dei linguaggi di programmazione sono a concatenazione
all'indietro. Data un'interrogazione cercano una dimostrazione costruttiva che
stabilisca una qualche sostituzione che soddisfi l'interrogazione. Un esempio
chiarirà meglio: supponiamo di voler dare delle regole sul concetto FAMIGLIA:
indichiamo il fatto che x è padre di y con: padre(x,y):
Possiamo subito scrivere un'altra regola del tipo: figlio(x,y) padre(z,x) AND padre(z,y)
ciò vuol dire che se x è fratello di y allora z è il padre
sia di x che di y.
A questo punto possiamo anche definire: zio(u,y) padre(z,y) AND fratello(z,u)
dove se u è lo zio di y allora z è padre di y e z è fratello di u.
Infine si può anche scrivere banalmente: fratello (x,y) fratello(y,x)
Questo sistema di regole va accompagnato ad una
base di conoscenza, come la seguente: fratello(Marco,Francesco)
padre(Cesare,Francesco)
fratello(Cesare,Antonio)
figlio(Antonio,Filippo)
Ciò che accade è che il PROLOG genera un albero riassuntivo tipo quello in figura 4 che rappresenta tutti i legami che le regole stesse hanno generato tra le variabili del problema.
Tutte queste regole sono sufficienti a far diventare il sistema in grado di dare risposte a domande del tipo
Chi è il fratello di Francesco? Posto nella forma Fratello( Francesco, x )
Il sistema risponderà: x = Marco
Oppure: Antonio è lo zio di Francesco?
Che formalmente si scrive : zio(Antonio, Francesco)
Risposta: SI
Invece se poniamo la seguente domanda: Padre(Cesare, Marco)
Sebbene dalle regole scritte sopra si deduce che la risposta è vera, il PROLOG non saprà rispondere poiché necessita di un'ulteriore regola come questa: fratello(x,y) --> padre(z,x) AND padre(z,y)
Il che porterà alla conclusione che Cesare è il padre di Marco. Tale aggiunta non è banale poiché è l'unica regola che consentirà di dedurre che quando x e y sono fratelli allora hanno lo stesso padre!
Un tale sistema di ragionamento è utile anche per la dimostrazione di teoremi e linguaggi di programmazione. Altri sistemi di ragionamento sono: Sistemi a frame e reti semantiche e Sistemi di logica descrittiva.
Un'alternativa è l'approccio a concatenazione in avanti, nel quale non vi sono interrogazioni.
Invece le regole di inferenza vengono applicate alla base di conoscenza, portando a nuove asserzioni. Questo approccio si ripete all'infinito o fino a quanto non viene soddisfatto un qualche criterio di fermata. L'idea è: ad ogni ciclo aggiungiamo le percezioni alla base di conoscenza ed eseguiamo il concatenatore in avanti, che scegli un'azione da eseguire concordemente con un insieme di regole condizione-azione.
Sistemi più complessi, spesso ibridi, chiamati gusci (shell) di sistemi esperti rientrano nella famiglia di interpreti generali che utilizzano sistemi di produzioni.
A seconda del tipo di problema vi è un diversa classificazione dei sistemi di produzione.
Qualora un problema non prevede alcuna modifica interna alle proprie regole e parametri (problemi senza backtracking) vengono adattati i Sistemi di Produzione di tipo commutativi, che si distinguono in:
Sistemi di Produzione monofonici, quando l'applicazione di una regola non impedisce l'applicazione successiva di un'altra regola già precedentemente selezionabile.
Sistemi di Produzione parzialmente commutativi. Data una sequenza di operazioni che trasformano uno stato x in uno stato y, il risultato dell'applicazione di tali regole è lo stesso ottenuto anche da una qualunque permutazione lecita delle stesse regole.
Nei problemi in cui possono avvenire modifiche ai parametri interni (problemi con backtraking) si adattano i Sistemi di Produzione parzialmente commutativi ma non monotoni.
Sistemi di Produzioni VS Programmi Tradizionali
Le principali caratteristiche che differenziano i programmi tradizionali e i sistemi di produzioni sono riassunte in tabella.
|
|
Programmi tradizionali |
Sistemi di produzioni |
|
|
Sono costituiti da una sequenza fissata di istruzioni |
Consistono di un insieme di regole indipendenti |
|
Strategia di controllo |
Non presente, o distribuita nel codice e nei dati, cioè unita al controllo |
Separata dal controllo, contenuta nelle regole di base e nella memoria di lavoro |
|
Controllo |
Predeterminato ed esplicito |
Non esplicito, ma determinato durante il run-time dalla catena delle azioni |
|
Esecuzione |
Segue le direzioni di struttura di controllo di inferenza |
Computata da una macchina |
|
Efficienza |
Alta |
Bassa |
|
Modificabilità |
Bassa |
Alta |
|
Trasparenza |
Molto bassa |
Molto alta |
|
Techiche di sviluppo |
Ciclo di vita di un normale software |
Sviluppo incrementale (Prototyping) |
Pro e contro del sistema di produzioni
Pro:
Molto facile e naturale da usare, adeguate dal punto di vista cognitivo;
Molto modulari
Hanno un ottimo grado di modificabilità e adattamento;
molto efficienti nei processi KA
sono di tipo dichiarativo, quindi il controllo globale è determinato dall'interprete
complessità di tipo lineare
Contro:
Inefficienti sotto alcuni aspetti (90% del tempo è speso nel confronto)
La computazione spesso non è trasparente
Non molto espressivi: troppo uniformi composti da strutture troppo piccole;
La loro programmazione astratta rende illeggibili le regole di base.
Il backtracking non viene spesso utilizzato, risultando essere più efficienti, ma suscettibili di effetti negativi, se non distruttivi, sulle eventuali modifiche della memoria di lavoro.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025