l'USO (tecniche di costruzione dei programmi);

PROGRAMMI

I programmi sono descrizioni dei metodi da seguire per risolvere un problema, cioè sono la descrizione di un ALGORITMO.

ALGORITMI

Un algoritmo è una sequenza di azioni che porta alla risoluzione di un problema.

Le caratteristiche di un algoritmo sono:

ogni azione deve essere svolgibile in tempo finito (l'esecuzione dell'intero algoritmo può però anche essere infinita;

deve avere una sequenza finita di comandi

COMANDI

I comandi sono azioni del linguaggio e sono chiamati anche enunciati, statement o istruzioni.

SINTASSI DEI COMANDI

comando di assegnazione (o assegnamento):

nome = espressione;

esempio: x = 3+5; ok

3+5 = x; NO

comando di blocco (unisce comandi diversi in un unico comando) :

esempio:

comando condizionale:

if (condizione) comando else comando

dove condizione è un'espressione di relazione che è vera o falsa.

Esempio: if (x>0) x=3; else

comando iterativo:

while (condizione) comando

dove condizione è un'espressione di relazione che è vera o falsa ed è detta GUARDIA, mentre il comando è detto CORPO DEL WHILE.

Se la guardia è vera si esegue il corpo del while finchè non diventa falsa. L'esecuzione può quindi anche essere infinita.

È impossibile sapere se un algoritmo finirà o no: questo problema è detto "problema della terminazione" (e se qualcuno lo risolve avrà una cattedra assicurata in qualsiasi università del mondo a suo desiderio e non avrà sicuramente più problemi di soldi!!!!)

Esempio:  while (x>0)

LA SEMANTICA DEI COMANDI

I comandi vengono eseguiti su uno STATO.

Uno STATO è un insieme di associazioni del tipo: (nome, valore) oppure (nome valore)

I vari comandi modificano lo stato corrente sul quale si applicano.

Vediamo alcuni esempi:

ES 1: ASSEGNAZIONE

Stato corrente :

x = 3+5;   questo comando dice che bisogna modificare l'associazione di x nello stato con l'espressione indicata nell'assegnazione.

Lo stato risultante è quindi :

x = x+5;   bisogna valutare il comando nello stato corrente, nel quale la x vale 3. Il nuovo valore da associare alla x è quindi 3+5=8.

Il risultato è perciò:

ES 2: BLOCCO

Stato corrente:

prima effettuiamo l'assegnazione alla x, cui dobbiamo associare 8 (3+5), portandoci così in una configurazione intermedia fatta così:

. È su questo stato intermedio che va svolta la seconda assegnazione presente nel comando blocco. L'esecuzione dell'assegnamento alla y ci porta nello stato finale: .

ES 3: COMANDO CONDIZIONALE

Stato corrente:

if (x>3) x = x+1; else x = x-1;   la condizione va valutata nello stato corrente. In questo caso essa è vera, quindi si effettua l'assegnazione x = x+1, associando a x 6 (5+1). Lo stato finale è: .

ES 4: ITERAZIONE INDETERMINATA

Stato corrente:

while (x>0) la guardia è vera nello stato, quindi si esegue il corpo del while. Così facendo ci portiamo nel seguente stato intermedio: . A questo punto dobbiamo ancora una volta verificare se la guardia è vera o falsa e, visto che essa è vera, eseguiamo ancora il corpo portandoci nello stato , che è lo stato finale, poiché in questo stato la guardia è falsa e non dobbiamo quindi eseguire il corpo del while.

SINTASSI DEL LINGUAGGIO DI PROGRAMMAZIONE

Esistono due aspetti per definire la sintassi:

RICONOSCITIVO

GENERATIVO

Vediamoli con ordine.

ASPETTO RICONOSCITIVO:

AUTOMI A STATI FINITI

Definizione grafica:

a

b

c

a, b, c sono dette ETICHETTE, o simboli del linguaggio

indica lo stato iniziale dell'automa

le altre frecce sono dette ARCHI o TRANSIZIONI.

Definizione matematica:

S = insieme degli stati dell'automa

A =     insieme delle transizioni: il primo numero indica lo stato di partenza, l'ultimo lo stato in cui si arriva se l'automa legge la lettera scritta nel mezzo.

I = 0  stato iniziale

Gli automi a stati finiti sono strumenti che riconoscono se una stringa appartiene oppure no al linguaggio, controllando se essa è sintatticamente corretta.

Gli automi sono strutture matematiche con un determinato numero di stati e archi che rappresentano le possibili transizioni fra uno stato e l'altro.

Per fare un esempio pratico, costruiamo un automa che descrive il funzionamento di un ascensore che va dal piano terra al primo piano e viceversa:

P1

P1

PT

PT

Un linguaggio è dato dall'unione di DIZIONARIO e SINTASSI.

Un dizionario è un alfabeto di simboli, cioè l'insieme delle basi per costruire le frasi del linguaggio.

Una sequenza di tali simboli è una STRINGA, la quale deve necessariamente avere un numero finito di simboli.

Se la stringa è riconosciuta dall'automa, essa appartiene al linguaggio riconosciuto da quell'automa.

Ma come fa un automa a riconoscere o meno una stringa?

In un automa ci sono degli stati particolari, detti FINALI o D'ACCETTAZIONE. Se, dopo aver analizzato simbolo per simbolo tutta la stringa l'automa si ferma su uno stato d'accettazione, significa che la stringa è riconosciuta e che quindi appartiene al linguaggio, altrimenti no.

In modo formale:

UNA STRINGA è RICONOSCIUTA DALL'AUTOMA SE E SOLO SE ESISTE UNA SEQUENZA DI STATI S0, S1, ., Sn TALI CHE S0 è LO STATO INIZIALE E Sn è STATO D'ACCETTAZIONE E ESISTE UNA TRANSIZIONE TRA UNO STATO E L'ALTRO.

Gli automi visti finora sono DETERMINISTICI in quanto hanno, per ogni stato, al più un arco uscente per la solita etichetta. Esistono però altri tipi di automi che non hanno questa proprietà specifica e si chiamano AUTOMI NON DETERMINISTICI.

Gli automi deterministici sono un sottoinsieme dei non deterministici, i quali sono quindi di numero maggiore.

CORRISPONDENZA FRA AUTOMI DETERMINISTICI E NON DETERMINISTICI

Per alcuni automi ND possiamo costruire l'equivalente automa deterministico (equivalente = che riconosce il medesimo linguaggio).

Per farlo dobbiamo prendere i sottoinsiemi degli stati dell'automa non deterministico: essi saranno gli stati del nuovo automa.

Esempio:

a 

a b

come si vede lo stato d'accettazione è lo stato 2, dallo stato 0, stato iniziale, escono due archi etichettati entrambi con il simbolo a. Le stringhe riconosciute da questo automa sono quelle che iniziano con una sequenza di a e finiscono con una b.

per ottenere l'automa deterministico costruiamo con una tabella i sottoinsiemi degli stati:

stati    simboli letti

a b

/

/ /

dopo aver costruito la tabella posso disegnare l'automa deterministico

a b

a

NB. Dopo la trasformazione, gli stati finali dell'automa deterministico sono tutti quelli che contengono almeno uno stato finale dell'automa non deterministico da cui deriva.

ASPETTO GENERATIVO

GRAMMATICHE LIBERE DA CONTESTO: le grammatiche sono strumenti matematici formali e si dicono "libere da contesto" perché le categorie sintattiche si possono espandere quanto si vuole, indipendentemente da ciò che sta loro intorno, cioè il loro contesto, appunto. Questo risulterà più chiaro andando avanti nello studio della materia.

Le componenti di una grammatica sono :

Un ALFABETO, o INSIEME DEI SIMBOLI TERMINALI

Le CATEGORIE SINTATTICHE, o INSIEME DEI SIMBOLI NON TERMINALI

Esempio: costruiamo la grammatica che definisce il linguaggio delle espressioni numeriche su N.

<Exp> <Num> | <Exp> + <Exp> | <Exp> - <Exp>

<Num> <Cif> | <Num><Cif>

<Cif>

la freccia si legge "è definita come."

<Exp>, <Num>, <Cif> sono categorie sintattiche,cioè simboli non terminali.

In particolare <Exp> è detto simbolo DISTINTO o anche simbolo iniziale

Ciascuna definizione presente nella grammatica è detta PRODUZIONE.

Per definire le stringhe del linguaggio generate dalla grammatica utilizziamo il

METODO CON STRUTTURA AD ALBERO

Un albero è un grafo con nodi ed archi dotato delle seguenti proprietà:

È ACICLICO

Ogni nodo ha AL PIU' un arco ENTRANTE

I grafi sono CONNESSI, cioè esiste sempre un collegamento fra le varie parti

Il nodo che non ha NESSUN ARCO ENTRANTE è detto RADICE

I nodi che non hanno NESSUN ARCO USCENTE sono detti FOGLIE e contengono solo simboli terminali

In particolare i nodi dell'albero devono sempre essere etichettati con simboli (o terminali o non terminali) e la radice deve contenere il simbolo distinto della grammatica.

Facciamo un semplice esempio: data la grammatica seguente

<S> ab | a<S>b

che riconosce le stringhe formate da una sequenza di a seguita da una sequenza di b della medesima lunghezza, costruiamo l'albero di derivazione per la stringa aabb

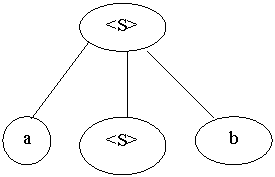
Come si vede,

i discendenti di un

nodo etichettato con una

categoria sintattica

contengono i simboli

di una produzione per

quella stessa categoria.

Potremmo anche utilizzare la struttura degli alberi di derivazione per verificare la semantica, ma dobbiamo fare attenzione: una GRAMMATICA PUO' ESSERE AMBIGUA! In questo caso è possibile costruire diversi alberi di derivazione per la stessa stringa e ciò ci porterebbe in errore nel controllo della semantica.

Il modo più comune per rendere non ambigua una grammatica che lo è , è aggiungere una o più categorie sintattiche. Non esiste un algoritmo prefissato per farlo, quindi ci vuole un po' d'ingegno..

Esistono però dei linguaggi che sono INTRINSECAMENTE AMBIGUI, cioè che possono essere definiti soltanto da grammatiche ambigue!

CONFRONTO FRA GRAMMATICHE E AUTOMI A STATI FINITI

LE GRAMMATICHE LIBERE SONO EQUIVALENTI AGLI AUTOMI A STATI FINITI ?

NO: le grammatiche sono più potenti.

Cioè esiste almeno un linguaggio generato da una grammatica libera che non può essere riconosciuto da nessun automa a stati finiti.

SE UN LINGUAGGIO E' RICONOSCIUTO DA UN AUTOMA, ALLORA E' ANCHE GENERATO DA UNA GRAMMATICA REGOLARE, E VICEVERSA.

SE UN LINGUAGGIO E' GENERATO DA UNAGRAMMATICA LIBERA MA NON REGOLARE, ALLORA ESSO NON E' RICONOSCIUTO DA NESSUN AUTOMA.

Le grammatiche regolari sono una sottoclasse delle grammatiche libere con una particolare struttura. Vediamo un esempio.

a b

a b

la grammatica corrispondente a questo automa è la seguente:

<0> a<1>

<1> a<1> | b<2> | b

<2> b<2> | b

come si vede le produzioni consistono nella coppia "simbolo letto <nuovo stato>" e anche nel solo simbolo letto, ma soltanto se nella produzione compare uno stato d'accettazione dell'automa

SISTEMI DI TRANSIZIONE

Un sistema di transizione è la generalizzazione di un automa a stati finiti.

DIFFERENZE FRA AUTOMI E SISTEMI DI TRANSIZIONI:

Nei sistemi di transizioni gli STATI possono essere anche INFINITI

" " possono esistere PIU' STATI INIZIALI

Gli STATI FINALI non sono di accettazione come per gli automi, ma sono gli stati DA CUI NON SI PUO' EFFETTUARE ALCUNA TRANSIZIONE

Un sistema di transizione è formato da tre componenti.

le CONFIGURAZIONI, che equivalgono agli stati degli automi

le CONFIGURAZIONI FINALI, un sottoinsieme delle configurazioni

le RELAZIONI DI TRANSIZIONI.

Spesso un sistema di transizione è formato da più regole, dette METAREGOLE, le quali possono rapprsentare in modo finito infinite transizioni.

Le metaregole spesso hanno questa struttura:

PREMESSE

Regola da applicare

Se ci sono le premesse

In questo caso la regola viene applicata se e solo se  valgono tutte le premesse.

Esistono due tipi di sistemi di transizioni:

BIG STEP (o SISTEMA DI SEMANTICA NATURALE): non ci sono configurazioni intermedie, ma attraverso chiamate ricorsive del sistema stesso nelle premesse si arriva direttamente alla configurazione finale

SMALL STEP ( o SISTEMA DI VALUTAZIONE): si arriva alla configurazione finale attraverso passi e configurazioni intermedie. Non ci sono chiamate ricorsive nelle premesse, tutto è svolto in modo iterativo.

INTRODUZIONE ALLA SEMANTICA DEI COMANDI IN JAVA

La grammatica dei comandi di Java (per semplicità il linguaggio Java è stato un po' modificato) è:

Com Ide = Exp; | Block | if (Exp) Com else Com

Block

Stat_list Com | Decl | Com Stat_list | Decl Stat_list

Decl int Ide; | boolean Ide; | int Ide = Exp; | boolean Ide = Exp;

Ide a | b |..| z

(per semplicità sono state omesse < e > e vengono considerati solo i tipi booleani e interi, la grammatica delle espressioni rimane invariata eccetto per la seguente produzione : Exp Num | Exp Op Exp | Ide

Op

Dove * = moltiplicazione e % = modulo, cioè il resto della divisione intera.

Il simbolo = non significa uguaglianza, ma il comando d'assegnamento, l'uguaglianza in java viene indicata col doppio uguale [= =])

FRAME E PILE DI STATI

Per capire cosa succede nel computer durante l'esecuzione di un programma, consideriamo come esempio il seguente blocco:

y = x}

ogni blocco che si apre provoca il crearsi di un FRAME, una funzione, inizialmente non definita, che associa ad ogni identificatore un valore.

Nel punto indicato da il frame è così costituito:

y

x

Nuovo frame

Con l'apertura del blocco più interno si forma un nuovo frame che si va a posizionare sopra a quello precedente:

Y X

Vecchio frame

Y X

Z

La prima assegnazione del blocco interno dichiara una nuova variabile z cui assegna il valore 25, mi porto nella seguente situazione:

A questo punto la seconda e ultima assegnazione mi dice che devo andare a cercare il valore di z per darlo a y. Quindi scendo nella pila per trovarlo.

Y X

Z

Adesso devo tornare in cima alla pila di frame e scendere come ho fatto prima per trovare la y, cui devo dare il valore di z, 25. Mi vengo a trovare quindi nella seguente situazione:

Adesso il blocco più interno si chiude e scompare anche il frame più in alto.

Mi rimane da fare l'ultimo assegnamento: y = x; ed ecco cosa succede nel frame:

	Y X

Come abbiamo visto, ogni blocco costruisce il proprio stato.

Rimane comunque una relazione fra i vari blocchi e i rispettivi stati: gli stati vengono messi uno sopra l'altro ( "A PILA").

OPERAZIONE PUNTO

Poniamo :

Ð insieme delle funzioni Ide Val, dove Val = valore naturale; cioè l'insieme delle funzioni che associano ad ogni identificatore il corrispondente valore n appartenente a N, insieme dei numeri naturali.

E insieme di tutte le pile di stati

§ la pila vuota

definiamo ora l'operazione punto (.): essa è una funzione che ha dominio Ð * E e dà come risultati E, cioè:

. : Ð*E E

X

esempio:

F'

Y Z

pila di frame

F

F  e F' sono frame e la pila di frame è lo STATO.

Come si vede graficamente, lo stato è costituito da uno STECK di FRAME.

Indicheremo con S lo steck, che è perciò costituito da:

S = F' . F .

S perciò è una funzione che appartiene ad E (si ricorda che E è l'insieme di tutti gli steck di frame).

Indefinita se S = § (cioè se S è un frame vuoto)

S(x) =     F(x) se S = F . S' e F(x) non è indefinito

S'(x) se S = F . S' e F(x) è indefinito

S' indica la pila rimanente sotto il primo frame F.

In termini letterari abbiamo definito la funzione S(x) nei seguenti termini:

il valore di x nello stato è indefinito se lo stato è costituito da un frame vuoto.

Il valore di x nello stato è il valore associato ad x nel frame più in alto (F) se tale valore esiste.

Il valore di x va cercato negli steck rimanenti sotto a F, se questo non associa alcun valore per l'identificatore x, cioè se F(x) è indefinito.

Questa definizione è ricorsiva e risulta più chiara facendo degli esempi:

EX

Poniamo S = F' . F. §

Dove F e F' sono così definite:

F' =

F = NB: SI RICORDA CHE IN JAVA NON E' POSSIBILE DICHIARE DUE VARIABILI CON LO STESSO NOME ANCHE SE IN BLOCCHI DIVERSI COME IN QUESTO CASO, MA NOI FAREMO FINTA CHE SI POSSA PER ASSICURARCI D'AVER CAPITO BENE IL PROCEDIMENTO E IL FUNZIONAMENTO DELLO STECK DI FRAME IN CORRISPONDENZA DEI BLOCCHI.

Trovare il valore delle seguenti variabili:

S(x) = F' (x) = 25   [poiché il primo valore associato alla x che troviamo scendendo nello steck è quello presente in F', il frame più in alto. ]

S(y) = (F. §)(y) = F(y) = 5    [poiché F'(y) non è definito dobbiamo cercare il valore di y nel frame sottostante che è F]

S(z) = (F . §)(z) = §(z) = valore indefinito [ poiché F'(z) non è definito dobbiamo cercare il valore di z nel frame sottostante (F). Neanche lì z è definita, quindi scendiamo ancora nello steck e raggiungiamo il frame vuoto (§). Dalla definizione ricorsiva data precedentemente, quando cerchiamo il valore di un identificatore su uno steck vuoto il risultato è indefinito ].

Nel gergo informatico, quando un identificatore non è definito in un frame, si dice

Che il risultato è BOTTOM. Naturalmente esisterebbe un simbolo per questa nozione ma non sono riuscita a riprodurre l'intero alfabeto greco sulla tastiera (per lo stesso motivo ho usato lettere normali come F o S per indicare i frame e lo steck).

LA SEMANTICA DEI COMANDI DI JAVA: LA MODIFICA DI STATO

ASSEGNAZIONE:

prendiamo uno stato F =

dopo l'assegnazione x = y; mi porto in un nuovo stato F' poiché è stato modificato il valore di una variabile, in questo caso la x:

F' =

DESCRIZIONE DELLA MODIFICA DI STATO PER UNA SOLA ASSEGNAZIONE:

F [10/x] = F MODIFICATO PER UNA SOLA ASSOCIAZIONE CHE E' DESCRITTA FRA LE PARENTESI QUADRE. QUESTA NOTAZIONE SIGNIFICA CHE PRENDO LO STATO F E CAMBIO L'ASSOCIAZIONE PER X, CUI GLI DO IL VALORE 10.

In termini di definizione di funzione il cambiamento di stato è:

V   se p = x

F[v/x](p) =  

F(p) se p != x

Dove v è un valore naturale, x è la variabile la cui associazione è stata modificata e p

Rappresenta un qualsiasi identificatore di cui si vuole cercare il valore nello stato

Modificato: se l'identificatore cercato è proprio x il suo valore è v; altrimenti il suo valore va ricercato tramite le regole descritte in precedenza.

ESEMPI:

F =

F [15/x](x) = 15

F[15/x](y) = F(y) = 10

F(x) = 5

(F[15/x]) [7/x] (x) = 7 lo stato modificato viene nuovamente modificato. Naturalmente quello che conta è l'ULTIMA MODIFICA.

(F[15/x]) [7/x] (y) = F(y) = 10

MODIFICA DEL FRAME

F[5/x, 6/y] = (F[5/x])[6/y]

Queste due espressioni sono equivalenti ma la migliore è la prima perché più veloce.

Questo tipo di scrittura però va bene solo se le due variabili da modificare sono diverse perché le modifiche nelle stesse parentesi vengono effettuate contemporaneamente:

F[5/x,6/x] NON DENOTA NESSUNO STATO: E' SBAGLIATO!!

Definizione:

§ se S = §

S[v/x] = F[v/x] . S'   se S = F . S' e F(x) non è indefinito

F . S'[v/x] se S = F. S' e F(x) è indefinito

REGOLE SEMANTICHE PER I COMANDI DI JAVA

D'ora in poi si sottointende che x appartiene all'insieme degli identificatori (Ide), che E è un'espressione (definita dalla categoria sintattica Exp) e che C è un comando (categoria sintattica Com).

Darò per scontato il sistema di transizione exp che associa ad ogni simbolo numerico il suo rispettivo valore naturale.

Definiamo ora il sistema di transizione com che definisce la semantica, cioè il significato, dei principali comandi di Java.

La semantica qui trattata è soltanta quella DINAMICA. Non ci interessiamo quindi agli errori dovuti ai tipi ( per esempio l'assegnamento int a = true; che associa ad una variabile intera un valore booleano). Questi tipi di errori sono controllati e valutati dalla semantica STATICA, che noi non tratteremo.

ASSEGNAMENTO

<E, S> exp v   

<x = E; , S> com S[v/x]

IF

<E, S> exp tt <C, S> com S'

<if (E) C else C', S> com S'

<E, S> exp ff <C', S> com S'

<if (E) C else C', S> com S'

WHILE

<E,S> exp ff   

<while (E) C, S> com S

<E, S> exp tt <C, S> com S'

<while (E) C, S'> com S'' 

<while (E) C, S> com S''

NB: NON è POSSIBILE SAPERE SE QUESTO COMANDO TERMINA OPPURE NO perché RICHIAMO LO STESSA SISTEMA DI TRANSIZIONE ( com) SULLO STESSO COMANDO WHILE IN STATI DIVERSI: PRIMA S, POI S'.

LA FINE DEL PROGRAMMA DIPENDE DA S'. SE L'ESPRESSIONE DI GUARDIA NELLO STATO S' E' FALSA IL PROGRAMMA TERMINA, ALTRIMENTI NO.

BLOCCO

<S-list, w . S> com F . S' NB: w E' UNO STECK PER ORA VUOTO

<{S-list, S> com S' CHE SI è CREATO IN SEGUITO ALLA

APERTURA DEL BLOCCO. ESSO VIENE MODIFICATO SOLO IN SEGUITO A DICHIARAZIONI DI VARIABILI ALL'INTERNO DEL BLOCCO. QUANDO LA PARENTESI GRAFFA SI RICHIUDE IL BLOCCO E' FINITO E w, CHE SI ERA EVENTUALMENTE MODIFICATO DIVENTANDO UN FRAME NON VUOTO (F) VIENE CANCELLATO. PER QUESTO IL RISULTATO FINALE E' SOLO S MODIFICATO DA EVENTUALI COMANDI PRESENTI NEL BLOCCO.

GLI OGGETTI

In Java un oggetto è l'unione di ASSOCIAZIONI variabile valore e METODI, cioè i possibili comportamenti dell'oggetto.

Le caratteristiche degli oggetti sono:

DINAMICITA': gli oggetti possono essere creati in qualsiasi momento e non vengono cancellati quando si esce dal blocco in cui sono stati creati ( a differenza delle associazioni che abbiamo visto finora). UNA VOLTA CHE E' STATO CREATO, UN OGGETTO RIMANE VIVO PER TUTTA L'ESECUZIONE DEL PROGRAMMA.

Gli oggetti vengono memorizzati nella MEMORIA HEAP, non sullo steck di frame. Questo dipende semplicemente dalla loro natura dinamica, che non permette loro di essere allocati su un frame che poi viene cancellato. Sul frame si formano soltanto dei riferimenti al luogo della memoria heap dove sono stati creati gli oggetti, in modo che sia possibile accedervi, non l'oggetto stesso.

ESEMPIO: x, y = variabili d'istanza dell'oggetto

Locazione nella memoria

heap

metodi