Teorema di Noether

fisica

Teorema di Noether

Se č invariante sotto trasformazioni , allora il sistema lagrangiano di Lagrangiana,

ha Integrale primo:

 

Dim

Considero una soluzione dell'equazione di Lagrange per e mostro che lungo questa soluzione    č costante. Per la proprietā di invarianza della trasformazione , si ha:

 

Quindi in forma differenziale (ponendo =):

0

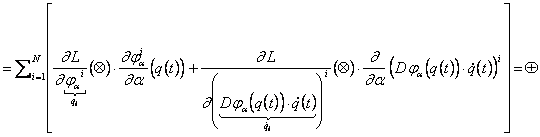
Tenendo conto che:

,

,

allora:

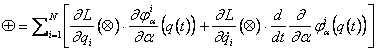
Si noti che finora vale tutto .

Dal fatto che renda invariante la, secondo la, non possiamo assolutamente sapere che la č soluzione dell'Eq. di Lagrange quando ; l'unica cosa che so č che č soluzione per.

In pratica non so se risolve l'Eq. di Lagrange perquando; so che la risolve per .

Pongo ora e uso l'Equazione di Lagrange .

=

=

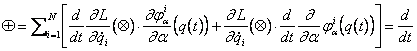
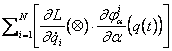Quindi:

costante.

CVD