Teorema Di Bernoulli - Dimostrazione

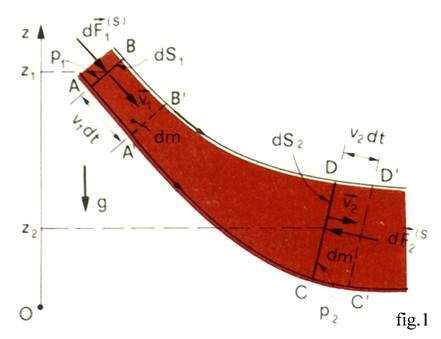
Assumiamo che nel tubo di flusso le velocità non varino da punto a punto della stessa sezione normale e che non si generino movimenti vorticosi per azione di variazioni brusche di sezione e direzione.

Forze in gioco

La massa fluida della zona ABCD all'istante t si muove per azione delle forze di volume (per ipotesi la sola forza di gravità), e delle forze di superficie agenti sulle superfici di base del volumetto dS₁ e dS₂, da parte del fluido esterno al volume ABCD. Se il fluido è ideale⁽¹⁾ non sono presenti sforzi di taglio generati per attrito interno sulla superficie tubolare laterale, ma sforzi normali da parte del fluido esterno. Per effetto di questi il fluido che, all'istante t, occupava il volume ABCD, occuperà il volume A'B'C'D' all'istante (t+dt). Per l'equazione di continuità, la massa dm₁ relativa al volume ABA'B' è uguale alla massa dm₂ contenuta nel volume CDC'D'. Posto ρ la massa volumica del fluido perfetto, deve risultare:

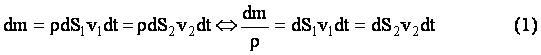
applicazione del teorema energia - lavoro

Consideriamo la variazione di configurazione realizzatasi nell'intervallo dt. Il lavoro compiuto dalla forza di gravità poichè la massa contenuta nel volume A'B'CD non cambia quota è pari a quello relativo allo spostamento di una massa dm dalla quota z₁ alla quota z₂. Tale lavoro  vale:

Per calcolare il lavoro delle forze di superficie, indichiamo con n₁ e n₂ i versori delle normali a dS₁ e dS₂, orientate positivamente verso l'interno della massa fluida. Le forze agenti su dS₁ e dS₂ possono, dunque, esprimersi come:

e i lavori compiuti da esse sono rispettivamente:

Il segno meno nella seconda relazione della (4) è dovuto al fatto che lo spostamento v₂dt è di verso opposto alla normale n₂. Il lavoro delle forze di superficie, esercitate verso l'interno del volume ABCD sulle sezioni dS₁ e dS₂ da parte del fluido esterno vale:

Il lavoro delle forze di superficie sul mantello tubolare è nullo perchè su questo le forze sono ovunque ortogonali agli spostamenti. La variazione di energia cinetica interve-nuta nell'intervallo di tempo dt, per la stazionarietà del moto, risulta⁽²⁾:

Tenendo conto delle (2), (5) e (6), il teorema energia-lavoro⁽³⁾ (dW^(g)+dW^(S) = dK) assume la seguente forma:

In virtù della (1), dividendo per dm e moltiplicando per ρ ambo i membri della (7), otteniamo la seguente relazione:

Poichè la (8) sussiste per ogni sezione normale del tubo di flusso considerato, il teorema di Bernoulli afferma che, lungo una generica linea di corrente di un tubo di flusso, nelle stesse condizioni sopra ipotizzate, la quantità:

considerazioni finali

Nel caso statico la (8) fornisce la legge di Stevino⁽⁴⁾. La somma (p+ρgz) dei primi due termini della (9) rappresenta, quindi, la pressione che sarebbe presente in una sezione anche nel caso statico ed è indicata con il nome di pressione statica. Il termine (1/2)ρv² rappresenta invece l'incremento della pressione in una sezione del tubo di flusso per effetto del moto ed è detta pressione dinamica. Dividendo ambo i membri per ρg, la (9) può anche scriversi:

I termini della (10) rappresentano delle altezze:

z è l'altezza geometrica della sezione considerata, cioè la distanza del suo centro rispetto all'origine O;

p/ρg è l'altezza di una colonna di fluido uguale a quello nel tubo di flusso che produce una pressione idrostatica pari a p ed è detta altezza piezometrica;

v²/2g è la cosidetta altezza d'arresto, cioè l'altezza massima cui giungerebbe un grave lanciato verso l'alto con velocità iniziale v.

Il teorema di Bernoulli si può enunciare dicendo che nel moto stazionario di un fluido ideale lungo un tubo di flusso la somma delle altezze geometrica, piezometrica e d'arresto è invariante lungo una qualsiasi linea di flusso. 

note

Un fluido dicesi ideale o perfetto se:

ogni sua porzione abbia volume, e quindi densità ρ, indipendenti dalla pressione a cui è sottoposto; ovvero è incomprimibile;

il coefficiente di viscosità η sia nullo, e pertanto gli sforzi di taglio generati per attrito interno tra le particelle di fluido sono nulli;

Nella configurazione iniziale l'energia cinetica complessiva è data dalla somma di due termini relativi alle masse contenute, nell'istante t, nei volumi ABA'B' ed A'B'CD:

Nell'istante finale (t+dt), in modo analogo, l'energia cinetica totale sarà:

Se il fluido si trova in condizioni stazionarie, fissato comunque un punto dello spazio, le velocità dei volumetti di fluido che via via nel tempo transitano per esso sono sempre le stesse; perciò le quantità al secondo membro della (1A) e della (2A) non dipendono (fissata la loro posizione) dall'istante in cui le si calcola. La differenza fra il valore finale e quello iniziale dell'energia cinetica del volume di fluido considerato sarà pari a:

Il teorema Energia-Lavoro, o teorema dell'energia cinetica afferma che il lavoro compiuto su di una particella, che si sposta dalla posizione A alla posizione B, dalla risultante delle forze è pari alla variazione dell'energia cinetica della particella stessa:

Se il fluido è a riposo, v₁=v₂=0 e la (10) diventa:

ossia:

che è proprio la nota legge di Stevino. Pertanto la statica dei fluidi, come già osservato per le particelle materiali, rappresenta un caso particolare della dinamica dei fluidi.