PRIMO PRINCIPIO DELLA DINAMICA - Sistemi inerziali e non inerziali

E' inerziale un sistema con origine nel Sole e orientamento costante rispetto alle stelle fisse;ed è inerziale ogni sistema che si muova rispetto a questo di moto traslatorio rettilineo ed uniforme.

Nel nostro sistema solare il Sole è un sistema di riferimento inerziale,mentre la Terra rappresenta quello,possiamo dire, "relativamente" non inerziale,in quanto la Terra pur avendo una velocità di rotazione,questa è talmente piccola,che in pratica,le deviazioni del principio di inerzia sono osservabili soltanto se si eseguono misure di grande precisione. Quindi con buona approssimazione,i sistemi di riferimento terrestri possono essere considerati inerziali,anche se ogni oggetto è sottoposto almeno alla forza peso.

Prima di Galileo si pensava che, per mantenere un corpo in moto rettilineo uniforme, occorresse una forza. Osservazione che invece va riferita a corpi che non sono liberi. Secondo il principio d'inerzia, invece, la forza necessaria, a mantenere in moto rettilineo e uniforme un corpo, serve per compensare le forze frenanti (tipo attrito) e, che una volta eliminate, danno la possibilità al corpo di mantenere la sua velocità costante. Ecco perché in auto è consigliabile mettere le cinture di sicurezza. Quando l'automobile incontra un ostacolo decelera bruscamente. I passeggeri, invece, continuano per inerzia a muoversi alla stessa velocità cui stava viaggiando l'autom 212c21c obile e, quindi senza cinture, vanno a sbattere contro il parabrezza.

In un sistema di riferimento non inerziale invece ,si hanno accelerazioni a cui non corrispondono cause reali. Se ad esempio ci trovassimo in un'automobile con un pilota dalla guida un po' spericolata, potremo renderci conto che, quando il pilota frena qualcosa ci spinge in avanti, quando accelera qualcos'altro ci preme contro lo schienale e, quando invece, curva a sinistra ci sentiamo spinti verso destra. Ciò che avvertiamo, in sostanza, sono delle forze, ma non vengono esercitate da alcun

agente; esse, infatti, sono solo la diretta conseguenza che il sistema non è più inerziale; queste forze sono dette forze apparenti o d'inerzia. Quindi, un sistema è non inerziale quando un corpo, inizialmente in quiete, comincia poi a muoversi spontaneamente; possiamo esser certi, allora che in gioco ci sono delle forze.

Forze fittizie o apparenti

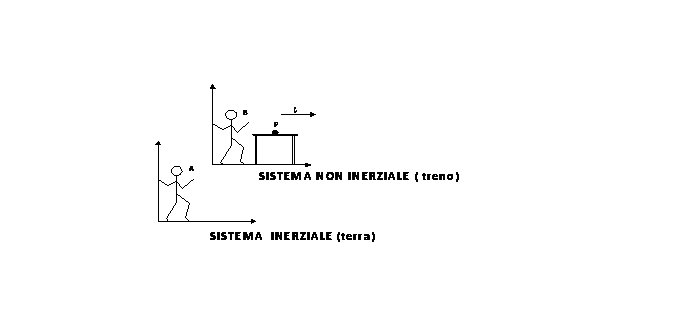
Consideriamo un sistema di riferimento (un treno) che si muove di moto rettilineo uniforme rispetto alla terra. Sul treno c'è una palla da biliardo P su un tavolo liscio, e un osservatore B; poiché il treno si muove con velocità v uniforme, la biglia resta in equilibrio.

Da terra l'osservatore A inerziale vede che il punto P si muove di moto rettilineo uniforme con velocità uguale a quella del treno.

Immaginiamo che il treno subisca una frenata. Dal punto di vista dell'osservatore A, se il punto materiale, essendo libero e non vincolato, non viene fermato e continua a muoversi con la stessa velocità v. dal punto di vista di B, invece, è che la biglia subisce un'accelerazione: il punto P, infatti, comincia, dallo stato di quiete, a muoversi. Ovviamente, egli crede che in gioco ci siano delle forze, nonostante non ci sia alcun sistema fisico nell'ambiente che lo permetta. Queste, appunto, sono le forze apparenti o fittizie.

È confermato che comunque siano delle forze, perché per poter annullare il movimento del punto, ad esso deve essere applicata una forza, che per l'osservatore A questa serve per frenare P e contemporaneamente il treno; mentre per l'osservatore è una forza che consente al punto P di restare fermo e, quindi, equilibra l'effetto della forza di inerzia.

L' Esperimento di Focault (pendolo) in cui fu dimostrato che posto un pendolo in un laboratorio,il suo piano di oscillazione ruota attorno ad un asse verticale con il passare del giorno. In realtà il piano di oscillazione che ha innanzitutto orientamento fisso nel sistema solare,ruota si, ma con esso anche tutto il laboratorio e la Terra.

A questo proposito introduciamo il principio di relatività,che ci consente di capire meglio l'esperimento. Dato un sistema di riferimento inerziale ,ogni altro sistema di riferimento si muove rispetto al primo di moto traslatorio rettilineo e uniforme,ed è per questo anch'esso inerziale.

Se analizziamo il moto di due sistemi che mantengono l'orientamento degli assi in modo costante,si dice che si muovono di moto traslatorio uno rispetto all'altro.

Quindi in un certo intervallo di tempo il punto subisce uno spostamento anche tutti gli altri punti del sistema lo subiscono.

Un altro caso di moto traslatorio tra due sistemi è il moto traslatorio rettilineo e uniforme;cioè l'origine del sistema si muove di moto rettilineo e uniforme (es. come un vagone del treno sulle rotaie).

SECONDO PRINCIPIO DELLA DINAMICA

Il secondo principio della dinamica (quella parte della fisica che studia le relazioni tra il moto dei corpi e le cause che lo determinano) ci rapporta ad una lunga serie di studi che sono stati ultimati con la definizione (operativa) del concetto di forza, alla quale si è giunti con la specificazione dello strumento che permette di misurarla: questo è il dinamometro; che è in grado di riportare le deformazioni prodotte dalla forza (e di definirla, quindi, staticamente, in quanto esso non considera il movimento causato da essa).

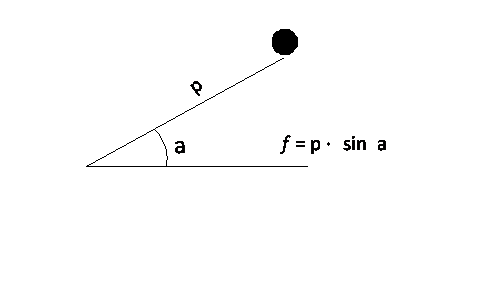Introduciamo, quindi le osservazioni di Galileo che, studiando il moto, su un piano inclinato levigato, di un punto materiale sotto la spinta di una molla, verificò che la risultante delle forze agenti sul punto materiale, è proporzionale al seno dell' angolo di inclinazione, e tangenziale al piano di inclinazione. Quindi, il modulo di f è costante (ovviamente può variare se cambia l'ampiezza di α); in questi casi si può misurare l'accelerazione, del moto del punto, in corrispondenza di valori diversi per la forza applicata, e si verifica, che :

= m ·

la proporzionalità tra forza e accelerazione è stabilita dal coefficiente m, che viene definito come massa inerziale (o gravitazionale). Notiamo, inoltre che, la forza è un vettore in quanto risulta essere il prodotto tra uno scalare (la massa espressa in Kg) e l'accelerazione (grandezza vettoriale il cui verso e direzione vanno a definire proprio quelli di f ).

C'è, però, ancora da capire perché la massa gravitazionale e quella inerziale risultano essere interscambiabili nella legge che definisce f.

La massa inerziale è definita come la "resistenza" che un corpo oppone alle variazioni di stato del moto, ovvero dipende dall'inerzia del corpo e, quindi, maggiore sarà l'inerzia, maggiore è la sua massa inerziale. La massa gravitazionale, invece, è la misura (ottenuta per confronto) del corpo come multiplo o sottomultiplo del chilogrammo.

Definendo la forza-peso, vediamo che essa è proporzionale alla massa gravitazionale e all'accelerazione gravitazionale, che varia leggermente in modulo a seconda del luogo terrestre in cui ci si trova (a causa della non perfetta sfericità della Terra) e che è sempre diretta verticalmente. Galileo, lasciando cadere due oggetti aventi forza-peso diversi tra loro, vide che essi giungevano al suolo contemporaneamente e, ne dedusse che, trascurando l'attrito dell'aria, il moto di caduta dei gravi, a parità di condizioni iniziali, ovvero a parità di velocità e spazio iniziali, è descritto dalla stessa legge oraria :

s = g · t²

v ottenuta integrando due volte l'accelerazione.

Per esempio, se abbiamo un punto materiale che viene lanciato verticalmente con velocità iniziale nulla (e sottoposto, quindi, alla sola accelerazione gravitazionale, trascurando gli attriti), si avrà che il moto, pur avvenendo nello spazio è però un moto monodimensionale, poiché il punto materiale si muove lungo la traiettoria definita dalla sola ascissa dell'ordinata. La coordinata z del punto ha, dunque, un'equazione oraria data da:

z (t) = h · ( − g · t² )

in quanto az − g (dove il segno - indica, appunto, che la direzione del moto è opposta a quella dell'asse z, facente parte di un sistema di riferimento destrogiro).

az − g vz (− g ) · dt + cost − gt + cost

dove la costante ₁ assume un valore nullo poiché abbiamo posto come condizione iniziale la velocità nulla.

z (t) = vz (t) · dt + cost = (− g) t · dt + cost =    − g · t² + cost ₂

considerando il fatto che g è una costante che vale g = 9,81 m/s² , cost ₂ è uguale alla quota iniziale.

Quindi siccome il peso è una forza sarà   = m

dove mg è la massa gravitazionale, ma si avrà anche p = i · a , proprio in quanto è una forza,e

pertanto

m mi da cui =

v dato che l'accelerazione è indipendente dall'oggetto (mg / mi ), è una costante e, quindi, mg e mi avranno le stesse dimensioni misurate in Kg, come g e a, la cui unità di misura, è invece, Kg · m/s².

È, inoltre, molto importante osservare che una conseguenza della proporzionalità tra massa gravitazionale e massa inerziale è il Principio di Equivalenza di Einstein, esplicato tramite un semplice esperimento concettuale : in un ascensore fermo c'è uno sperimentatore che lascia cadere una biglia; essa acquisisce, quindi, un'accelerazione pari a

Nel momento in cui, però, il cavo dell'ascensore si spezza, anche quest'ultimo si muoverà di moto uniformemente accelerato con accelerazione .

Pertanto l'ascensore (e quindi anche l'osservatore) non costituiscono più nel loro insieme un sistema inerziale, e quindi, la pallina risulterà ferma dal punto di vista dell'osservatore, poiché ascensore pallina e osservatore si muovono con la stessa accelerazione. Questo dimostra che qualunque corpo in un campo gravitazionale, sottoposto alla stessa accelerazione e che quindi il suddetto campo risulta annullato all'interno di un sistema di riferimento non inerziale, accelerato della stessa g.

PRINCIPIO DI RELATIVITA' GALILEIANA − TRASFORMAZIONI DI GALILEO

E MOTO RELATIVO

Il principio di relatività è uno dei principi fondamentali della dinamica. Esso è stato enunciato, per la prima volta, da Galileo nel suo " Dialogo sopra i massimi sistemi del mondo" e, poi, rimesso in critica da Einstein più tardi.

Questo enunciato mette in evidenza che, presi due sistemi di riferimento, è importante che le relazioni tra grandezze fisiche siano le stesse tra i due. In altri termini, secondo il principio di relatività, se uno dei membri di un'equazione fisica cambia passando da un sistema di riferimento all'altro, anche l'altro membro, per preservare la relazione di uguaglianza, deve cambiare coerentemente. Secondo la definizione di "Covarianza delle leggi fisiche": i due membri di un' equazione fisica devono essere covarianti passando da un sistema di riferimento all'altro che si muova di moto traslatorio rettilineo e uniforme. Il caso contrario è, invece, detto "Invarianza", cioè i membri restano immutati.

Consideriamo un sistema di riferimento S e un secondo sistema di riferimento S' che si muove, rispetto a S, di moto traslatorio rettilineo uniforme. Supponiamo che all'istante

t = 0 e che le origini coincidano e la velocità sia parallela all'asse x.

Preso un punto P sia il vettore posizione di P rispetto a S ed il suo vettore posizione rispetto ad S'. si ha:

+ OO' =

proiettando sugli assi possiamo scrivere:   

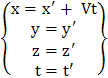
che rappresentano le trasformazioni di Galileo.

Derivando, rispetto al tempo, otteniamo :   

= +

Moto relativo

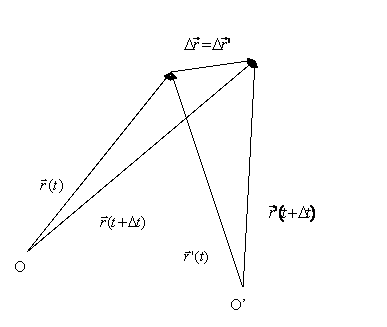
Due osservatori O ed O', solidali con sistemi di riferimento fermi tra loro, in generale individuano la posizione di un punto materiale in moto con due diversi vettori ed , ma misurano stessi spostamenti Δ = Δ e, quindi, stesse velocità ed accelerazioni. Essi vedono essenzialmente lo stesso moto.

Passando da un sistema di riferimento all' altro, le componenti di tutte le grandezze vettoriali cambiano secondo una stessa legge di trasformazione, mentre tutte le grandezze scalari, quali il modulo di un vettore, l'angolo tra due vettori, la massa di un corpo ecc. , restano immutate.

Quindi due osservatori in moto l' uno rispetto all' altro, i riferimenti cui essi sono solidali vengono detti in " moto relativo tra loro".

A questo punto gli osservatori dovranno conoscere le leggi con cui si trasformano le grandezze fisiche passando da un sistema di riferimento ad un altro. Solo così potranno tradurre i risultati delle misure effettuate in un sistema di riferimento, nei numeri che rappresentano i risultati delle stesse misure effettuate in un altro sistema.

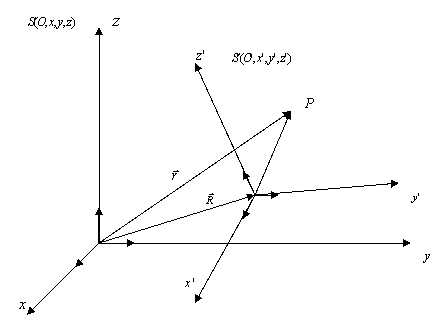
Un osservatore O in un sistema di riferimento S misurerà le coordinate x,y,z del punto P e vedrà come esse variano in funzione del tempo t misurato con un suo orologio. Sinteticamente S è costituito dall' insieme di queste grandezze e si indica con S(O,x,y,z,t).

Consideriamo allora due sistemi di riferimento in modo relativo l' uno rispetto all' altro: S'(O',x',y',z',t') ed S(O,x,y,z,t). Conoscendo il moto di S' rispetto ad S, sarà possibile determinare la descrizione del moto del punto P, che sarà data dall' osservatore O solidale con S.

Ognuno dei due osservatori O ed O' ha un proprio orologio con cui eseguire misure di intervalli di tempo. Se le velocità sono molto minori della velocità c della luce nel vuoto, gli orologi dei due osservatori una volta sincronizzati in un instante, resteranno sincronizzati

in tutti gli istanti successivi. Così il tempo diventa indipendente dal sistemo di riferimento e quindi diventa una "grandezza assoluta".

Riguardo alle leggi di trasformazione delle grandezze cinematiche, consideriamo due sistemi di riferimento S(O,x,y,z) ed S'(O',x',y',z'), in moto relativo qualsiasi fra loro, e supponiamo di conoscere il vettore posizione di un punto P, rispetto ad S'; supponiamo di conoscere, cioè, in un dato istante t , le coordinate, x',y',z' di P in S'. Detti i versori degli assi x',y',z' , il vettore si scrive:

= x'+ y'+ z' .

Siano i versori degli assi x,y,z del sistema di riferimento S e indichiamo con il vettore che individua l' origine O' di S' nel riferimento S.

Dette X,Y,Z , le coordinate di O' in S, nell' istante t , si ha:

= X + Y + Z

Dette x,y,z le coordinate di P in S, il vettore , che individua questo punto in S, si scrive:

= x + y + z

Dalla figura 2 risulta evidente che è dato da:

= + .

I tre versori , costanti nel sistema di riferimento S, sono , in generale, variabili nel tempo visti dall' osservatore solidale con S. Analogamente, i tre versori sono costanti per O e, in generale, funzioni del tempo per O'.

La relazione = + tra i vettori posizione ed vale, qualunque sia la disposizione relativa dei due riferimenti, in ogni dato istante e perciò è indipendente dal loro moto relativo. La legge di trasformazione delle velocità e delle accelerazioni, coinvolgendo variazione nel tempo, dipendono dal tipo di moto relativo tra i due riferimenti.

SISTEMA NON INERZIALE DOTATO DI MOTO TRASLATORIO

Consideriamo un sistema di riferimento fisso (inerziale) ed un sistema mobile (non inerziale); supponiamo che il sistema mobile si muove, rispetto al quello fisso, di moto traslatorio.

Se P, nel sistema inerziale, si muove per azione di una forza, allora possiamo scrivere:

= m ·

Le coordinate del punto P (x'y'z') nel sistema non inerziale sono legate a quelle dello stesso punto (xyz) nel sistema fisso.

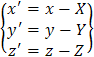
v dove X Y Z sono le coordinate dell'origine O del sistema mobile

Le coordinate x' y' e z' derivate una volta ci danno la relazione tra velocità di P (nei due sistemi):

e derivate una seconda volta, la relazione tra accelerazione, sempre del punto P (nei due sistemi):

= = =

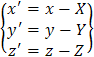
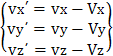
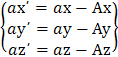
R , V e A sono vettore posizione, velocità e accelerazione dell'origine O del sistema mobile rispetto a quello fisso o di inerziale.

Essendo V la velocità del sistema non inerziale non costante, risulta che a' di P non è uguale ad a, differiscono infatti di A, ovvero:

= ; =

quindi:

− m · = m ·

L'osservatore mobile, misurando la quantità m · , troverà un risultato non uguale alla forza alla "forza reale" f , ma anche il termine ( − m · A ) detta, appunto, forza d'inerzia; essa sarà pari alla massa del punto materiale moltiplicata l'accelerazione, ma cambiata di segno.

Il termine A è detta accelerazione di trascinamento e, in questo caso moto traslatorio, è uguale per tutti i punti.

SISTEMA NON INERZIALE DOTATO DI MOTO QUALUNQUE

Il caso visto precedentemente è uno particolare, in cui il sistema di riferimento non inerziale si muove di moto traslatorio rispetto a quello fisso. Nel caso in cui il sistema non inerziale abbia moto qualunque,possiamo partire dalla relazione:

x' + y' +z' = (x - X) + (y - Y) + (z - Z)

Nella relazione non solo le coordinate X,Y,Z dell'origine (che si muove di moto non uniforme) non posso essere scritte come Vx t , Vy t, Vzt ,ma in più i versori i, j e k non sono costanti, e dunque la loro derivata temporale non è nulla, ma :  

· ·

v ω rappresenta la velocità angolare con cui il sistema mobile ruota rispetto a quello fisso.

Derivando la prima relazione rispetto al tempo, otterremo:

(vx - Vx (vy - Vy (vz - Vz

in termini vettoriali la relazione può essere scritta anche:

= − = - ( + · O'P )

La velocità del punto P rispetto al sistema mobile è detta velocità relativa ed è la relazione:

v' = v'x v'y v'z

La velocità assoluta è la velocità, invece, del punto P rispetto al sistema fisso ed è :

v = vx vy vz

Infine, la velocità di trascinamento è la velocità con cui si muove, rispetto al sistema fisso, il punto solidale col sistema mobile, considerato e occupato da P ed è:

vt + · O'P

v alla velocità V dell'origine O' è sommata la velocità ω · O'P con cui si muove l'estremo libero del vettore ruotante O'P ; inoltre, il punto P essendo solidale col sistema mobile la velocità v' è nulla.

Derivando, nuovamente, rispetto al tempo la relazione: (vx - Vx) + (vy - Vy) + (vz - Vz

si ottiene :

(ax - Ax (ay - Ay (az - Az

in termini vettoriali la relazione può essere scritta come :

= − − = − [ + · O'P + · ( · O'P ) ] - 2 ·

L'accelerazione del punto P rispetto al sistema di riferimento mobile è detta accelerazione relativa ed è la relazione:

= a'x a'y a'z

L'accelerazione assoluta è l'accelerazione del punto P rispetto al sistema di riferimento inerziale ed è :

ax + ay az

L'accelerazione di trascinamento è quella con cui si muove, rispetto al sistema fisso, il punto solidale col sistema non inerziale, considerato e occupato da P, ed è:

= + · O'P + · · O'P

v l'accelerazione di trascinamento è composto da tre termini: l'accelerazione A dell'origine O' del sistema mobile; l'accelerazione tangenziale di modulo · O'P | = α · d del moto circolare compiuto dall'estremo libero del vettore O'P e, infine, l'accelerazione radiale di modulo |ω · ω O'P | = ω² · d del moto circolare compiuto dall'estremo libero del vettore O'P.

Infine, è presente un'altra accelerazione, che è nulla solo quando v' = 0, cioè quando il punto P è in equilibrio nel sistema mobile. Questa è detta accelerazione di Coriolis o complementare ed è :

ac ·

v non è altro che il prodotto vettoriale tra il doppio della velocità angolare del sistema mobile e la velocità relativa del punto P.

Sostituendo nell' espressione : - m − m = m ·

L'accelerazione at, a differenza del moto traslatorio, è diversa da punto a punto del sistema mobile; ma accanto alla forza apparente di trascinamento - m at appare anche la forza di Coriolis − m = − 2 m · ·

v m rappresenta la massa che si muove con velocità v' rispetto al sistema di riferimento non inerziale e ω è la velocità angolare del sistema non inerziale misurata rispetto al sistema fisso.

La forza di Coriolis è indipendente dalla posizione del punto materiale, ma dipende dalla sua velocità.

TEORIA DELLA RELATIVITA' RISTRETTA

Come sappiamo il principio di relatività insieme alle trasformazioni di Galileo (che dimostra come le coordinate di un punto materiale cambiano da un sistema all'altro) associano le forze all'accelerazione,enunciando così il Secondo Principio della dinamica. Quindi una trasformazione dinamica covariante che non sarebbe tale se la forza fosse associata alla velocità. Anche perché abitualmente nelle trasformazioni di Galileo la velocità viene lasciata inalterata.

Quindi se consideriamo lo studio fatto finora come quello della meccanica classica,possiamo dire che

prendiamo in considerazione come principi basilari di questa "il principio di relatività" e quello di "invariata del tempo",riconoscendo il tempo come grandezza assoluta.

Questa teoria classica fu messa in crisi verso la fine del secolo da alcune osservazioni sulla propagazione della luce;in particolare dalle equazioni di Maxwell,che sintetizzano le leggi relative ai fenomeni elettrici e magnetici. Egli parla di una velocità assoluta,quindi non più di una velocità relativa a qualche sistema rispetto al quale misurare quella velocità.

Poi un altro esperimento,quello di Michelson indicava che la luce proveniente dal Sole è la stessa sia quando procede parallelamente alla Terra,sia in modo ortogonale. Mise in crisi in modo sperimentale l'effetto somma della velocità di Galileo.

Quindi qual è il sistema di riferimento della luce???

A quei tempi la tendenza era quella di rinunciare al principio di relatività,preferendo la possibile esistenza dell' "etere"individuato come sistema di riferimento privilegiato per i sistemi inerziali.

Einstein pubblicò la sua teoria sulla "relatività ristretta" che si basa su tre principi fondamentali:

Principio di relatività

Principio di costanza della velocità

Principio di conservazione della quantità di moto

Il primo e il terzo appartenenti già alla meccanica classica. Il principio di costanza della velocità che prese il posto della legge di trasformazione di Galileo,in contrasto con il Principio di costanza della luce.

Le trasformazioni di Galileo vennero perciò sostituite da Einstein con quelle di Lorentz.

Facendo riferimento alle trasformazioni di Galileo,sappiamo che v= v' + V, legge che è incompatibile con il principio di costanza della velocità della luce poiché perché esso possa valere t (diverso )t'. La grandezza tempo è basata su:

L' individuazione di un orologio,cioè uno strumento che compie cicli rigorosamente ripetitivi.

La capacità di giudicare il sincronismo degli eventi.

Il sincronismo è possibile quando due eventi a e b avvengono nello stesso posto.Se avvengono in due posti diversi non sarà possibile controllare contemporaneamente gli orologi, e anche se a e b avessero due osservatori si porrebbe il problema di sincronizzare gli orologi.In che modo?

La procedura più diffusa è quella del segnale orario(inviare agli orologi un segnale radio in modo che all'arrivo di esso possano partire con sincronismo).Ma questa procedura non è sempre applicabile,soprattutto in relatività,quando due sistemi si muovono con velocità prossime a quelle della luce.

Un metodo efficace è quello di disporre di un segnale elettromagnetico da un punto di mezzo C che arriva così ai due orologi. Ma il sincronismo degli orologi è una caratteristica relativa,in quanto se i due orologi sono localizzati in posti diversi appaiono non sincroni da un sistema in moto rispetto al primo.

Un raggio s di un orologio impiega un tempo Δt a compiere un'oscillazione

Δt =

dal punto di vista solidale ad esso.

Dal punto di vista del movimento, invece, il raggio compie un percorso più lungo, poiché mentre questo si muove (M) il rivelatore si sposta di un tratto RR'' = SS'' :

Δt' = =

SS'' = V · t' e SS' = e quadrando tutto si ha :

Δt' = · = Δt² + · t'²

Si deduce:

Δt' =

Il tempo Δt battuto dall'orologio mobile scorre più lentamente del tempo proprio

(fenomeno dilatazione tempo ).