LA CORRENTE ALTERNATA - CONDIZIONE DI PARTENZA

fisica

LA CORRENTE ALTERNATA

CONDIZIONE DI PARTENZA

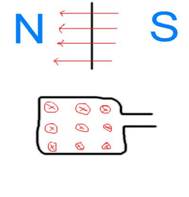
Immaginiamo di porre una spira di materiale conduttore ( ad esempio rame) all'interno di un campo magnetico come in fig. 1

Fig. 1 In nero è mostrata la spira inserita nel campo magnetico da due diverse visuali, in cui si nota come le linee di campo attraversino la superficie della spira ste 424f59e ssa ( disegnate in rosso).

2. CALCOLO DEL FLUSSO

Per calcolare la quantità del flusso del campo magnetico che passa all'interno della superficie della spira, si applica la definizione di flusso, in pratica:

Φ_S (B) = S * B * cosα (1)

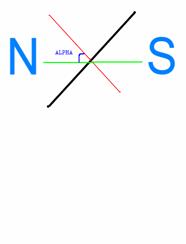
Dove per α s'intende l'angolo che si forma tra la normale alla superficie e le linee di forza del campo magnetico ( fig. 2)

Fig.2 E' mostrato un esempio di posizione della spira nello spazio dove è visibile l'angolo tra la normale alla superficie e le linee di flusso del campo magnetico.

3. APPLICAZIONE MOTO CIRCOLARE

Applicando un moto rotatorio alla spira, questa comincerà a ruotare intorno al suo asse con una certa velocità che è chiamata ώ.In questo modo, l'angolo tra la normale alla superficie e le linee di flusso del campo magnetico cambierà al passare del tempo. Per trovare come varia l'angolo in funzione del tempo, si parte dalla definizione di velocità angolare del moto circolare, vale a dire: ώ = ά/t, e la si esplicita rispetto ad ά.

Otterremo così che ά = ώ* t; sostituendolo nella formula (1) otterremo che il flusso del campo magnetico che attraversa la spira sarà uguale, al passare del tempo, ad:

Φ_s (B) = S * B * cosώt (2)

4. CONFRONTO CON MOTO ARMONICO

Gli scienziati, arrivati alla formula (2) si accorsero che era somigliante alla formula che esprimeva l'equazione di un moto armonico, cioè x = R * cosά, e pensarono che anche il flusso del campo magnetico potesse comportarsi come un moto armonico.

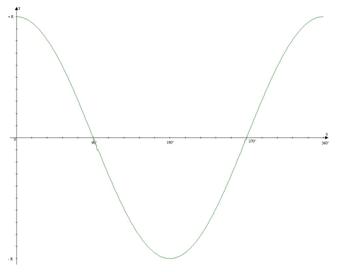
Il moto armonico, descritto nel grafico 1, è il moto di un corpo rispetto ad un punto medio e ha le seguenti caratteristiche:

Un' ampiezza chiamata R

Un periodo, cioè il tempo in cui avviene un ciclo completo.

Una pulsazione chiamata ώ

Una frequenza, cioè le oscillazioni per unità di tempo.

Fig.3 Grafico rappresentativo del moto armonico

Confrontandolo con il comportamento del flusso che attraversa la nostra spira in movimento, vedrò che anche lo stesso flusso si comporta seguendo il morto armonico; infatti:

Il flusso ha un'ampiezza massima uguale a S * B

Ha un periodo

Ha una pulsazione ώ

Ha una frequenza

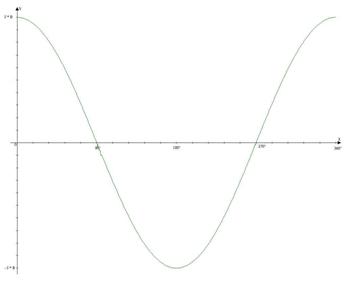
Fig.4 Grafico del moto armonico applicato alla spira in movimento nel campo magnetico. Sull'asse delle y è rappresentata l'intensità del flusso del campo magnetico.

Discorso a parte va fatto per la velocità: infatti, in un moto armonico la velocità non è costante, e questo è comprensibile se immaginiamo il moto armonico come la proiezione su una retta di un moto circolare.

Fig. 5 Proiezione su una retta del movimento di un corpo che segue il moto circolare.

.

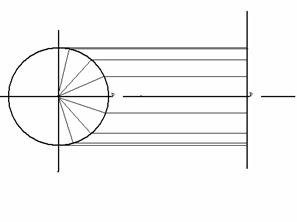
Un corpo che si muove sulla circonferenza percorrerà spazi uguali in tempi uguali, ma man mano che si allontanerà dal punto medio, le proiezioni sulla retta del suo spostamento saranno sempre più piccole, ma percorse sempre nello stesso tempo: questo implica una diminuzione di velocità. In conclusione il corpo allontanandosi dal punto medio decelera, avvicinandosi accelera. Quindi tracciando grafico caratteristico bisognerebbe " rallentare, quando ci si allontana dall'asse delle x, e " accelerare" quando ci si avvicina allo stesso.

5. CALCOLO MATEMATICO DELLA VELOCITA'

Capito teoricamente il concetto di velocità, bisogna chiarirlo matematicamente: per trovare la formula della velocità, possiamo sfruttare il grafico del moto armonico; infatti, trovare la velocità equivale ad ottenere la " tendenza" della funzione in un determinato punto, e per fare questo dobbiamo calcolare la derivata della stessa funzione.

Quindi partendo da x = R * cosά, la derivata sarà:

V = - Rώ * senώt (3)

Questa è appunto la formula che esprime la velocità in un moto armonico.

	Fig. 6 Andamento della velocità al passare del tempo in un moto armonico

6. APPLICAZIONE CONCETTO DI VELOCITA' A FLUSSO MAGNETICO.

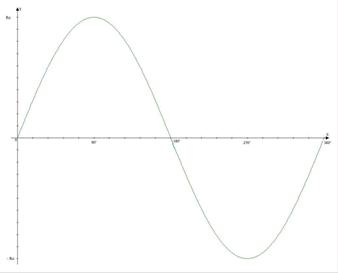
Partendo dal presupposto che il flusso del campo magnetico, sempre legato alla nostra spira in movimento, segua le leggi del moto armonico, trovare la velocità del moto armonico descritto dallo stesso flusso equivale a trovare la variazione d'intensità del flusso al passare del tempo, cioè v = Φ_s (B)/ Δt.

Utilizzando la formula (3), e sapendo che R = S * B ( semplice equivalenza tra le due ampiezze), ottengo che:

Φ_s (B)/ Δt = - S * B *ώ *senώt (4)

Fig. 7 Andamento del rapporto tra la variazione dell'intensità del flusso del campo magnetico il tempo.

7. CALCOLO FORZA ELETTROMOTRICE

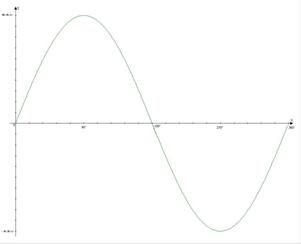
Una volta ottenuta la variazione dell'intensità del flusso al passare del tempo, posso calcolare la F.E.M. prodotta dalla stessa variazione applicando la legge di Lentz:

F.E.M = - Φ_s (B)/ Δt (5)

Ottengo che la F.E.M, nel mio caso, sarà uguale ad:

F.E.M = S * B *ώ *senώt (6)

	Fig.7 Variazione della F.E.M prodotta dalla rotazione della spira al passare del tempo.

8. INSERIMENTO SPIRA IN ROTAZIONE IN CIRCUITO OHMICO.

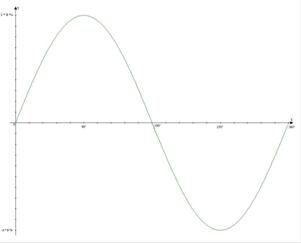
Per vedere in modo tangibile gli effetti della F.E.M creata dalla nostra spira in rotazione ( e dalla conseguente variazione di flusso del campo magnetico), dobbiamo collegare la stessa ad un circuito fatto di materiale ohmico, cioè che segue le leggi di Ohm.

Partendo dalla legge di Ohm per cui i = F.E.M. / R ( dove R indica la resistenza interna al circuito), sostituendo la formula (6) otteniamo che la corrente misurata nel circuito e prodotta sempre dalla spira in rotazione sarà uguale ad:

i = (S * B *ώ *senώt) / R (7)

Questa corrente ha la peculiarità di cambiare intensità ( al variare del tempo) e verso ( ogni semiperiodo): questa è la CORRENTE ALTERNATA.

9. RAPPRESENTAZIONE GRAFICA DELLA CORRENTE ALTERNATA.

Osservando l'equazione (7) si vede che il fattore che modifica l'intensità di corrente è il passare del tempo, perciò i fisici hanno riscritto questa formula ponendo

(S * B *ώ) /R = i_max (8)

ottenendo

i = i_max * senώt

che ha il seguente grafico caratteristico

	Fig.8 Rappresentazione della variazione d'intensità di corrente al variare del tempo.

10. CARATTERISTICHE DELLA CORRENTE ALTERNATA E CONFRONTO CON CORRENTE CONTINUA.

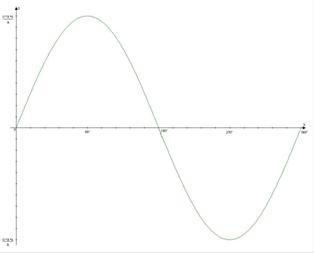
Dato che la corrente alternata segue l'andamento di un moto armonico, ne possiede automaticamente tutte le caratteristiche; quindi è possibile parlare:

di Frequenza di una corrente alternata

di Periodo

di Pulsazione

di Ampiezza

Per ogni possibile valore che può assumere l'intensità della corrente alternata, n'esiste uno equivalente di corrente continua: l'equivalenza segue la legge i_cont = i_alt / √2; i_cont è chiamato anche VALORE EFFICACE della corrente alternata.

Facendo un confronto più preciso, queste sono le principali analogie e differenze tra corrente alternata e corrente continua.

A)    Non è possibile l'elettrolisi con la corrente alternata, poiché gli ioni hanno una velocità di deriva molto alta, quindi non rispondono prontamente al cambiamento di polarità che è provocato ogni semiperiodo dalla corrente alternata. Perciò ad esempio ioni negativi che si dirigono verso il polo positivo, continuano a dirigersi verso lo stesso polo, anche se questo, nel frattempo, ha cambiato segno ( da + a -).

B) Anche la corrente alternata produce calore passando all'interno di un materiale conduttore.

C)    Non è possibile questo tipo di misurazione perché l'ago non riesce a seguire l'inversione di polarità semiperiodica dovuta alla corrente alternata.

D)    La corrente alternata, tramite l'effetto Joule, può rendere incandescente un materiale e provocare luminescenza, ma per far sì che un osservatore non noti la variazione periodica di intensità luminosa, la corrente alternata deve avere una frequenza elevata