|
|
| |
Relazioni di Elettrostatica
La forza elettrica è data dalla legge di
Coulomb : ![]() e 10-12 C2/Nm2
e 10-12 C2/Nm2
Il Campo elettrostatico è ![]() essendo Q la carica
di prova, quindi il campo non dipende dalla presenza di un'altra carica, per lo
meno non se parliamo di problemi statici, poiché se ci sono movime 727d37h nti di
cariche, il campo varia nel tempo e si producono effetti di induzione. In
generale il campo elettrostatico è un campo conservativo. Per un insieme
discreto di n cariche e per un insieme continuo abbiamo :
essendo Q la carica
di prova, quindi il campo non dipende dalla presenza di un'altra carica, per lo
meno non se parliamo di problemi statici, poiché se ci sono movime 727d37h nti di
cariche, il campo varia nel tempo e si producono effetti di induzione. In
generale il campo elettrostatico è un campo conservativo. Per un insieme
discreto di n cariche e per un insieme continuo abbiamo :
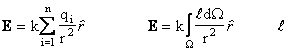 è la densità della
distribuzione delle cariche sul dominio W, in
generale poniamo :
è la densità della
distribuzione delle cariche sul dominio W, in
generale poniamo :
per le curve l densità lineare
per le superfici s densità superficiale
per i volumi r densità volumetrica.
Alcuni Campi Elettrostatici interessanti sono i seguenti :
#1 Asse di una Bacchetta : 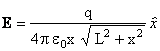 (per il filo
indefinito è :
(per il filo
indefinito è : ![]() )
)
#2 Asse del Disco : 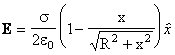 (per il piano
indefinito è :
(per il piano
indefinito è : ![]() )
)
#3 Asse di un Anello : 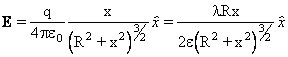
#4 Guscio
Sferico : per r >
R 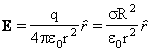
per r < R E è costantemente nullo. (Si ricava dal teorema di Gauss)
#5 Sfera carica uniforme : per r > R Come se la carica fosse tutta concentrata nel centro della sfera
per
r < R ![]()
#6 In un Condensatore : ![]() (È nullo all'esterno delle armature.)
(È nullo all'esterno delle armature.)
Il lavoro del campo su una curva c che va da A
a B è ![]()
Per il calcolo del potenziale abbiamo una certa simmetria con il campo elettrostatico, solo che al denominatore abbiamo solamente r al posto di r2 (e ovviamente V è una quantità scalare mentre E è un campo vettoriale).
Una relazione fondamentale è ![]()
Le principali equazioni derivanti dalla legge di Coulomb sono le seguenti
Teorema di Gauss : ![]()
Equazioni di Maxwell : ![]() (Mette in evidenza il
fatto che E è un campo conservativo).
(Mette in evidenza il
fatto che E è un campo conservativo).
![]() (Deriva
dal teorema di Gauss in forma differenziale).
(Deriva
dal teorema di Gauss in forma differenziale).
Nel calcolo del Potenziale usiamo quasi le stesse formule per quello del campo ossia :
![]() per i sistemi
discreti di cariche ;
per i sistemi
discreti di cariche ; ![]() per i sistemi continui
nel dominio W
per i sistemi continui
nel dominio W
Alcuni Potenziali importanti sono i seguenti.
#1 Asse di un Filo : 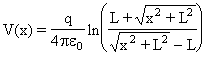 (Il filo è lungo
2L)
(Il filo è lungo
2L)
1.1 Filo indefinito : ![]()
#2 Asse del Disco : ![]()
#3
Piano indefinito : ![]() (Il termine
costante tende a infinito, ma nelle d.d.p. si semplifica).
(Il termine
costante tende a infinito, ma nelle d.d.p. si semplifica).
#4
Guscio Sferico : per r > R ![]() (Come
se fosse tutta nel centro).
(Come
se fosse tutta nel centro).
per r < R ![]()
#5
Sfera carica : per r > R ![]() (Come se fosse
concentrata tutta nel centro).
(Come se fosse
concentrata tutta nel centro).
per r < R ![]()
#6 Condensatore : ![]() (È costante al di fuori delle armature)
(È costante al di fuori delle armature)
La Capacità di un conduttore in equilibrio elettrostatico è data dalla formula
costante : ![]()
Per una Sfera
abbiamo : ![]()
Per un Condensatore : Piano : ![]()
Sferico ![]()
Cilindrico 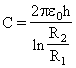
Chiamiamo U funzione potenziale e, in un campo conservativo come quello elettrostatico, rappresenta la quantità di lavoro che il campo può idealmente fare.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025