|
|
| |
FORZE
DEFINIZIONE DI FORZA. Le forze possono essere di varia natura (gravitazionali, elettriche, muscolari, magnetiche etc). Quello che adesso ci preoccupa è poter dire come ci accorgiamo che su un corpo sta agendo una forza , vedere cioè quali sono gli effetti misurabili dell'applicazione di una forza. Da questo punto di vista dobbiamo distinguere se i corpi sono liberi o vincolati. L'effetto di una forza applicata ad un corpo libero è la variazione del suo stato di moto, il corpo inizialmente fermo si muove, un corpo in moto cambia l'intensità della velocità o la sua direzione. Un corpo vincolato(che non può muoversi), sotto l'effetto di una forza si deforma( si allunga, si accorcia, cambia in genere la distanza fra due suoi punti). Dal punto di vista delle deformazioni distinguiamo i corpi in rigidi (non si deformano), plastici (si deformano e restano deformati), elastici (si deformano sotto l'azione della forza e tornano allo stato iniziale se cessa la forza). Naturalmente per 141c25b potere misurare le forze tramite le deformazioni ci dobbiamo servire dei corpi elastici. Due forze saranno eguali se applicate ad uno stesso corpo elastico provocheranno le stesse deformazioni.
E' utile notare che le forze per poter essere definite hanno bisogno oltre che dell'intensità, anche della direzione, del verso e del punto di applicazione. Non è la stessa cosa, gli effetti sono diversi, se spingiamo o tiriamo un corpo in senso orizzontale o verticale. Le forze sono cioè delle grandezze vettoriali. Definiremo in seguito il significato di grandezze vettoriali e grandezze scalari. Per adesso ci occuperemo di forze che hanno tutte la stessa direzione e lo stesso verso, quali sono le forze di gravitazione, comunemente chiamate peso e che agiscono su tutti i corpi presenti sulla terra e che sono sempre dirette verticalmente verso il basso.
Criterio di eguaglianza: Due corpi A e B avranno lo stesso peso, se applicati alla stessa molla disposta verticalmente provocheranno lo stesso allungamento e si potrà dire Pa=Pb.
Criterio di somma: Se due corpi A e B applicati contemporaneamente alla molla provocano lo stesso allungamento che si ha se si applica alla molla il corpo C sarà:
Pc=Pa+Pb.
A questo punto per potere misurare le forze ci serve definire il campione di forze. Potremo scegliere l'unità di misura di forza in modo indipendente dalle altre unità di misure, come il peso che ha un certo corpo in un determinato luogo. Dobbiamo precisare dove il peso del corpo che scegliamo è unitario, perché il peso del corpo, a differenza della sua massa varia a secondo della sua posizione rispetto alla superficie terrestre. Infatti se appendiamo alla stessa molla lo stesso corpo a livello del mare o a 7000m di altezza, l'allungamento della molla sarà diverso, maggiore al livello del mare e minore a 7000m. Ciò significa che il peso del corpo, che è la forza con cui il corpo è attratto dalla terra è maggiore al livello del mare e minore a 7000m di altezza.
Nel sistema di unità di misure pratico, che è un sistema diverso da SI, il campione di forze è scelto come il peso a cui è sottoposto il cilindro di platino e iridio( lo stesso che serve a definire il campione di massa), a livello del mare e a quarantacinque gradi latitudine e ad esso si dà il nome di chilogrammopeso Kgp. Nel sistema internazionale l'unità di misura di forza è derivata ed è il Newton N (1N=9,806 Kgp.). In seguito si vedrà meglio la definizione di N.
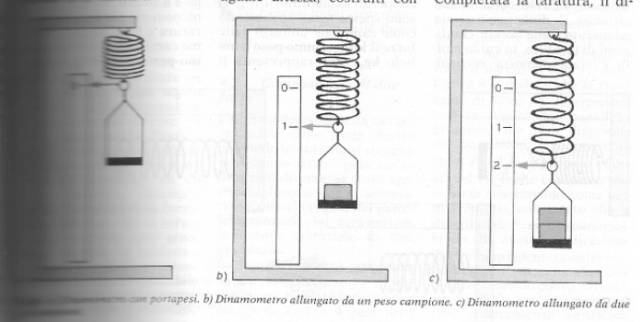
DINAMOMETRO.
Per costruire un dinamometro,misuratore di forza,abbiamo bisogno di una molla disposta perpendicolarmente e di un regolo parallelo alla molla. All'estremità della molla si fissa un indice che scorre sul regolo. Se alla molla non è applicato nessun corpo la forza sarà zero, quindi sul regolo in corrispondenza dell'indice segneremo 0. Se applichiamo alla molla il corpo il cui peso è unitario, la molla si allunga e in corrispondenza della nuova posizione dell'indice sul regolo segneremo 1Campione. Se appendiamo alla molla due campioni ,in corrispondenza dell'indice segneremo 2 campioni e così di seguito.
ALLUNGAMENTI DI UNA MOLLA E FORZE APPLICATE.
Si è detto che le forze applicate ad una molla provocano un allungamento. Che relazione esiste fra forze applicate( causa) e allungamenti della molla (effetti) Per dare una risposta a questo quesito si può fare il seguente esperimento.
Si prenda una molla e la si disponga verticalmente. Accanto si disponga un regolo millimetrico, munito di un indice triangolare che può scorrere lungo il regolo, come in figura.
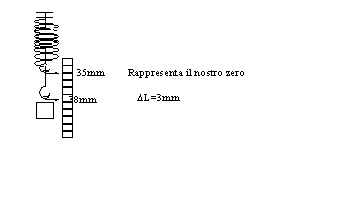
Si faccia coincidere l'indice con l'estremità della molla(il gancio) e si annotino i millimetri corrispondenti sul regolo (ad es 35mm). Si appende alla molla un corpo di cui si conosce la forza peso, la molla si allunga. Portiamo l'indice in corrispondenza della nuova posizione del gancio e si leggono i millimetri corrispondenti sul regolo (ad. Es. 38mm). La differenza ci dà l'allungamento subito dalla molla ( es 38mm-35mm=3mm).Si ripete l'operazione per un certo numero di pesi. Ad ogni peso corrisponde un determinato allungamento. I valori vengono riportati in tabella con i relativi errori. Dalla tabella si passa, come al solito al grafico ed unendo i vari punti si ottiene una retta passante per l'origine degli assi. Le due grandezze sono direttamente proporzionali e il loro rapporto, tenendo conto degli errori di misura è costante (vedi tabella e grafico). La costante, che cambia se varia la molla ci dà la forza per unità di allungamento ed è chiamata costante di elasticità.
|
F(gp) |
|
err ass(gp) |
DL(mm) |
|
err ass(mm) |
F/DL(gp/mm) |
|
err ass |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
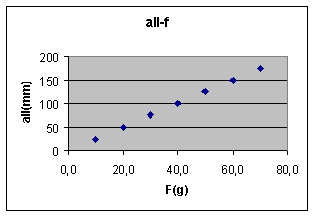
La molla del nostro esempio ha una costante di elasticità pari 0,40(gp/mm)+-0,02(gp/mm), il che vuol dire che se si allunga di 1mm la forza è di 0,40gp. Se vogliamo esprimere la costante nel SI dobbiamo passare dai gp ai N e dai mm ai m.
1gp = 0,001Kgp =10-3Kgp =9,8*10-3N ; 1mm=0,001m =10-3m;
0,40gp/mm=0,40*9,8*10-3N/10-3m =3,9N/m.
Ogni molla ha la sua costante di elasticità e segue la legge F=K*DL fino ad un certo valore di forza applicata e si dice, entro questi valori di forza, perfettamente elastica. Aumentando i valori delle forze applicate, la molla perde prima la perfetta elasticità, quindi diviene anelastica o plastica(non torna, cessata la forza alla sua lunghezza iniziale) e infine superato un certo valore si rompe.
SOMMA DI FORZE (REGOLA DEL PARALLEGRAMMA)
Abbiamo già detto che una forza è perfettamente definita (conosciuta) se oltre al suo valore si sa la direzione il verso e il punto di applicazione. Due forze possono avere la stessa intensità ma direzioni diverse e quindi non essere eguali. L'intensità è la misura della forza , il punto di applicazione è il punto in cui la forza è applicata , la direzione è la retta lungo la quale la forza agisce (parallelamente alla superficie terrestre, perpendicolare o formare con la superficie un certo angolo). Un volta stabilita la direzione vi possono essere due versi (se la direzione è perpendicolare alla superficie terrestre la forza può agire verso il basso o verso l'alto).
Tutte le grandezze, che come le forze hanno bisogno per la definizione di quattro elementi(intensità,punto di applicazione,direzione e verso) vengono chiamate grandezze vettoriali, mentre le grandezze come la massa, la lunghezza, il tempo, la densità, che, per essere definite, hanno bisogno solo dell'intensità sono chiamate grandezze scalari. Per sommare le grandezze scalari si ricorre alla somma aritmetica della loro intensità. Per le grandezze vettoriali bisogna nella somma tener conto anche della direzione e non si possono sommare semplicemente le loro intensità.
Le forze come tutte le grandezze vettoriali sono rappresentabili con dei vettori, che sono dei segmenti orientati , la cui lunghezza dipende dall'intensità, la retta di cui sono parte rappresenta la direzione, la freccia il verso, il punto iniziale il punto di applicazione.
![]()
Due forze applicate allo stesso punto si annullano (il loro effetto è zero e quindi se il punto era fermo resta in equilibrio), se esse hanno la stessa intensità, la stessa direzione e verso opposto.
![]()
![]()
Due forze eguali e contrarie hanno come somma zero e saranno rappresentate da due vettori che giacciono sulla stessa retta, della stessa lunghezza e di verso opposto.
Applichiamo ad uno stesso punto materiale tre forze in modo che il punto resti in equilibrio. La risultante delle tre forze è nulla e quindi la somma delle prime due è eguale ed opposta alla terza.
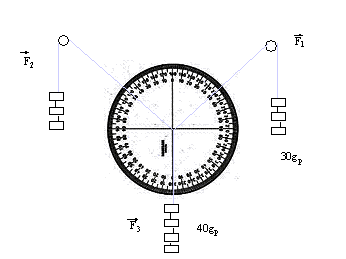
La forza F3 ha direzione perpendicolare rispetto alla superficie terrestre ed è diretta verso il basso. La direzione delle forze F1 e F2 può essere determinata , misurando l'angolo che i fili formano o con la direzione perpendicolare o con la parallela alla superficie terrestre.
Le tre forze possono essere rappresentate da tre vettori seguenti.
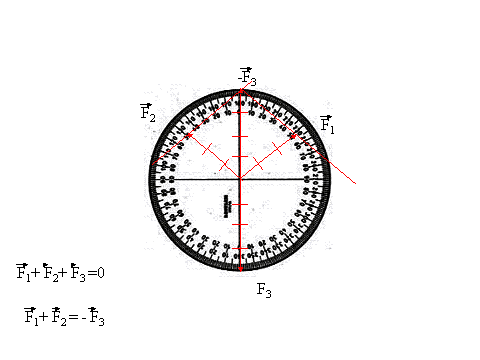
Il vettore che si ottiene ribaltando il vettore F3, costruendo cioè la forza eguale e contraria a F3, è la somma (risultante) di F1 e F2 . Se uniamo le punte di F1 e F2 con la risultante otteniamo un parallelogramma che ha come lati consecutivi le forze che si devono sommare e come diagonale la risultante.
Le forze, come tutte le grandezze vettoriali, si sommano perciò con la regola del parallelogramma. Si disegnano i vettori rappresentanti le forze con lo stesso punto di applicazione e dall'estremità del primo si traccia la parallela al secondo, dall'estremo del secondo la parallela al primo. Si ha così un parallelogramma. La risultante sarà la diagonale che ha come punto iniziale il punto iniziale dei due vettori.
L'operazione inversa della composizione (somma) di forze (da due ne otteniamo una, risultante , che ha gli stessi effetti delle due) è la scomposizione. Da un'unica forza ne troviamo due con determinate direzione e verso e che sommate mi danno proprio la forza scomposta. All'unica forza posso sostituire le due componenti, ottenendo gli stessi effetti. Per scomporre , una volta stabilita la direzione e il verso delle componenti, dall'estremità della forza si tracciano le parallele alle due direzioni. Queste parallele incontreranno le due direzioni in due punti e così sulle due rette che rappresentano le due direzioni avrò due segmenti che rappresentano i due lati consecutivi del parallelogramma e quindi le due componenti.
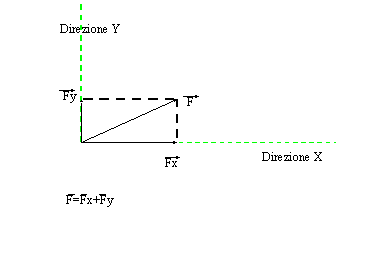
Fx e Fy sono le componenti della forza F lungo le due direzioni.
VINCOLI E REAZIONI VINCOLARI
Perché la molla una volta allungata resta in equilibrio? La forza ad essa applicata non si azzera(Ad esempio il peso del corpo non si annulla). Evidentemente sul corpo oltre al suo peso che tenderebbe a farlo muovere verso il basso agisce una forza eguale e contraria, in modo che la somma delle forze sia eguale a zero. Tale forza è dovuta proprio all'allungamento, tanto è vero che ,se togliamo il peso, sotto l'azione di questa forza l' estremità della molla ritorna nella sua posizione iniziale. La molla si oppone al movimento verso il basso creando una forza eguale e contraria al peso che farebbe avvenire il movimento che la molla non permette. La molla può essere considerato un vincolo. Il vincolo infatti è un mezzo che non permette o tutti i movimenti o alcuni movimenti, creando delle forze che annullano quelle forze che farebbero avvenire i movimenti da esso impediti. Tali forze sono chiamate reazioni vincolari.
Una superficie piana, liscia, priva di attrito impedisce tutti i movimenti ad essa perpendicolari, che farebbero entrare il corpo al suo interno. Se applichiamo al corpo una forza perpendicolare al piano verso l'interno, siccome tale movimento è impedito, il piano annulla questa forza, creando una forza(reazione vincolare) eguale e contraria alla forza applicata. Se invece al corpo,posto sul piano, applichiamo una forza parallela al piano, siccome i movimenti paralleli non sono impediti, il vincolo non crea nessuna reazione vincolare e il corpo sotto l'azione di tale forza si sposta.
PIANO INCLINATO
Una piano inclinato è una superficie piana rigida, che forma un'angolo diverso da zero e diverso da 90° con la superficie terrestre. Vi sono piani più e meno inclinati.
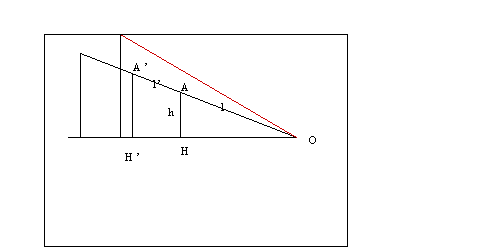
Per misurare l'inclinazione prendiamo sul piano un punto A e misuriamo l'altezza h=AH e la lunghezza l=AO. Se cambiamo il punto e consideriamo un altro punto A' cambierà l'altezza h' e la lunghezza l', non cambierà il rapporto altezza e lunghezza h/l=h'/l'. Infatti i triangoli AOH e A'OH' sono triangoli simili(hanno la stessa forma e gli angoli sono eguali) e i lati omologhi(lati opposti ad angoli eguali) sono in proporzione. Tale rapporto cambia solo se cambia l'angolo che il piano forma col piano orizzontale e misura perciò l'inclinazine del piano. L'inclinazione tende a zero quando il piano diventa orizzantale e ad 1 quando il piano diventa verticale. Se il piano è orizzontale h=0 e h/l=0. Se il piano è verticale AO coincide con AH, h=l , h/l=1.
Se poniamo sul piano un corpo su di esso agisce la forza peso P che è verticale rispetto alla superficie terrestre. Scomponiamo P in due componenti una parallela al piano, l'altra perpendicolare al piano P=Pn+ Ppar . Come detto al posto di P possiamo considerare le sue due componenti. Pn farebbe avvenire un movimento, che il piano impedisce ed è quindi annullata dalla reazione vincolare R. Ppar fa avvenire un movimento possibile e quindi sotto la sua azione il corpo scivola luno il piano. Se vogliamo che il corpo resti in equilibrio dobbiamo applicare una forza che chiameremo equilibrante e che deve esser eguale e contraria a Ppar. Quindi per tener fermo un corpo in una posizione del piano dobbiamo applicare una forza eguale e contraria alla componente parallela della forza peso. Ppar varia al variare di P e dell' inclinazione. Consideriamo i rettangoli AOH e O'PparP. Essi sono simili e perciò i lati omologhi stanno in proporzione.
Ppar:P =AH:AO; Ppar =P*h/L.
Se il piano diventa orizzontale h/l=0 Ppar =0, infatti il peso è perpendicolare al piano e non c'è componente parallela. Se invece il piano dinenta verticale h/l=1 Ppar =P. Infatti in questo caso la forza peso è completamente parallela al piano.
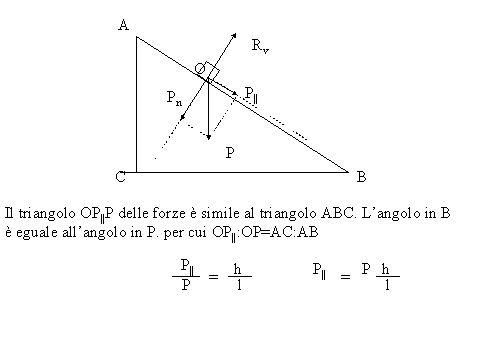
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025