|
|
| |
Da osservazioni sperimentali risulta che la capacità di un condensatore varia, qualora fra le due armature venga sostituito al vuoto (o aria) un materiale isolante, omogeneo e isotropo.
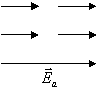
Consideriamo un condensatore piano, la cui capacità sia data dall'espressione: 222d32c
![]()
quando fra le armature c'è l'aria. Inserendo un materiale non conduttore, la capacità si modifica e risulta maggiore nel rapporto
![]()
![]() , così definita, è la costante dielettrica relativa del
mezzo.
, così definita, è la costante dielettrica relativa del
mezzo.
La nuova capacità può essere quindi espressa come:
![]()
![]()
Ricordiamo brevemente che un conduttore è un metallo la cui disposizione degli atomi del reticolo cristallino è tale da lasciare essenzialmente "liberi" alcuni elettroni (1 o 2 per atomo). L'energia caratteristica dell'interazione fra questi elettroni e il reticolo è piccola, inferiore all'energia termica.
In prima approssimazione tali elettroni
formano un "gas" e sotto l'azione di un campo elettrico si spostano venendosi
così a creare una separazione di cariche: tale movimento avviene finché il
campo elettrico interno ![]() (creato dalla
separazione delle cariche si
(creato dalla
separazione delle cariche si
oppone al campo ![]()
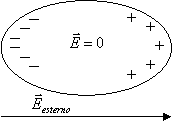 All'equilibrio "elettrostatico" il campo all'interno risulta nullo.
All'equilibrio "elettrostatico" il campo all'interno risulta nullo.
![]()
Il conduttore si è caricato in superficie.
Ne risulta un "movimento ordinato" nel tempo (concetto di corrente) se viene mantenuta una differenza di potenziale ai capi di un conduttore. Gli elettroni liberi sono detti di conduzione.
Gli isolanti, detti dielettrici sono
caratterizzati dall'avere atomi o molecole, con gli elettroni legati ai
rispettivi nuclei. Tali elettroni non sono liberi di muoversi sotto l'influenza
di un campo elettrico ![]() applicato. Tuttavia
avviene una separazione tra le cariche (+) e le cariche (-). Ne nasce un dipolo
indotto che si orienta nel campo.
applicato. Tuttavia
avviene una separazione tra le cariche (+) e le cariche (-). Ne nasce un dipolo
indotto che si orienta nel campo.
Molecola a simmetria sferica:
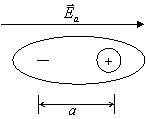
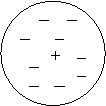
![]() (1)
(1)
momento di dipolo
Esistono molecole che hanno momento di
dipolo permanente derivante da una distribuzione asimmetrica di cariche. I
dipoli sono orientati in tutte le direzioni e il momento risultante è nullo. In
campo ![]() acquistano un momento
diverso da zero (es. molecole dell'acqua):
acquistano un momento
diverso da zero (es. molecole dell'acqua):
![]()
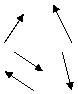
dipoli senza campo dal
loro allineamento nasce un campo ![]() che indebolisce il
campo applicato nel rapporto:
che indebolisce il
campo applicato nel rapporto:
![]()
I dipoli si orientano lungo il campo: sono sottoposti ad una coppia di momento
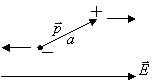
![]()
![]() (2)
(2)
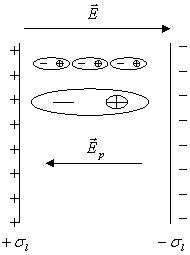 Si può supporre che le cariche adiacenti si elidano e rimanga un unico
dipolo con cariche
Si può supporre che le cariche adiacenti si elidano e rimanga un unico
dipolo con cariche ![]() e
e ![]() , cariche di "polarizzazione" che creano a loro volta
, cariche di "polarizzazione" che creano a loro volta ![]() che si sovrappone al
campo applicato
che si sovrappone al
campo applicato ![]() creato dalle
creato dalle ![]() (libere) sulle
armature.
(libere) sulle
armature.
![]()
Sono vettori // e discordi, avendo scelto un condensatore piano.
![]()
Poiché
![]() ;
; ![]()
![]() ; da cui
; da cui ![]()
Per trovare un legame tra ![]() e
e ![]() si definisce un nuovo
vettore polarizzazione
si definisce un nuovo
vettore polarizzazione ![]() = momento di dipolo
per unità di volume.
= momento di dipolo
per unità di volume.
![]() (3)
(3)
dove:
![]() numero atomi / volume
numero atomi / volume
Dimensionalmente:
![]()
Si può ipotizzare una dipendenza lineare di ![]() dal campo:
dal campo:
![]() (4)
(4)
dove:
![]() = suscettività
elettrica
= suscettività
elettrica
![]()
Si può quindi scrivere:
![]()
![]()
avendo posto ![]() costante dielettrica
relativa.
costante dielettrica
relativa.
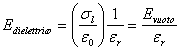
È uso indicare ![]() vettore spostamento (5)
vettore spostamento (5)
per cui ![]() non dipende dal
mezzo
non dipende dal
mezzo
![]() dipende dalla densità
di carica (es. sulle armature)
dipende dalla densità
di carica (es. sulle armature) ![]()
![]() dipende dalla densità
di carica di polarizzazione
dipende dalla densità
di carica di polarizzazione ![]()
![]() da entrambi
da entrambi
In un dielettrico valgono le leggi dell'elettrostatica salvo sostituire a:
![]()
Infatti esprimendo ![]()
poiché ![]()
![]()
e quindi ![]()
![]() (6)
(6)
In forma differenziale:
![]()
![]() (7)
(7)
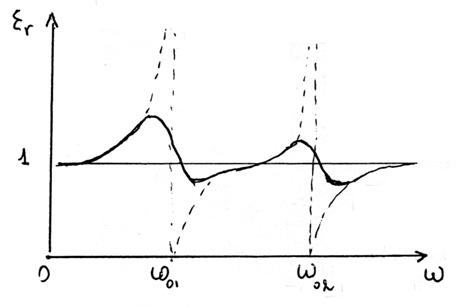
Andamento di ![]() in funzione della
frequenza
in funzione della
frequenza ![]() , dell'acqua, fase solida (a) e fase liquida (b):
, dell'acqua, fase solida (a) e fase liquida (b):
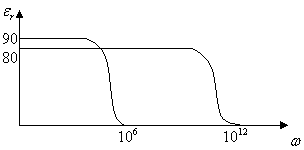
Per
frequenze ![]() o
o ![]() Hz
Hz ![]()
Le molecole non sono in grado di seguire l'alternarsi del campo
![]()
Si può notare nella figura che ![]() costante e poi cade a zero per frequenze
costante e poi cade a zero per frequenze ![]() o
o ![]() Hz.
Hz.
Lo stesso andamento
si ottiene per molecole non polari, che in presenza di ![]() assumono la forma di
dipolo.
assumono la forma di
dipolo.
Esistono infatti
molecole i cui ioni subiscono uno spostamento gli uni rispetto gli
altri, come ad esempio NaCl, tuttavia tali molecole sono abbastanza grandi,
hanno notevoli momenti di inerzia e all'aumentare della pulsazione del campo
applicato, ![]() , non sono più in grado di seguire l'alternarsi del campo: la
risposta, cioè la costante dielettrica (
, non sono più in grado di seguire l'alternarsi del campo: la
risposta, cioè la costante dielettrica (![]() ), crolla a zero.
), crolla a zero.
Invece gli
elettroni hanno piccola inerzia, possono seguire l'alternarsi del campo
fino a frequenze ottiche ![]() Hz. Vale a dire quando
si invia luce sul materiale, cioè (come sarà spiegato in seguito), un'onda
elettromagnetica il cui campo elettrico (e magnetico) oscilla con frequenze
appunto
Hz. Vale a dire quando
si invia luce sul materiale, cioè (come sarà spiegato in seguito), un'onda
elettromagnetica il cui campo elettrico (e magnetico) oscilla con frequenze
appunto ![]() Hz.
Hz.
Si può ricavare una espressione analitica dell'andamento della costante dielettrica in funzione della frequenza mediante un trattamento classico nel caso in cui gli elettroni di valenza o esterni sono legati al nucleo in modo isotropo (ovvero, quando le forze di richiamo tra elettroni spostati e nuclei sono sostanzialmente le stesse in tutte le direzioni dello spazio).
Possiamo introdurre un semplice modello meccanico per rappresentare il fenomeno: in figura gli elettroni sono legati al nucleo da "molle" con la stessa costante elastica.
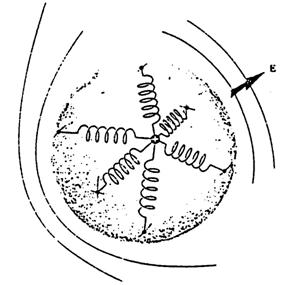
Si assume l'atomo formato da un nucleo positivo (+) e da una "nuvola" elettronica il cui centro (-) coincide con il nucleo.
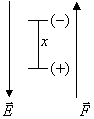 Applicando
Applicando ![]() il centro (-) si
sposta di un tratto
il centro (-) si
sposta di un tratto ![]() verso l'alto se il
campo è rivolto verso il basso.
verso l'alto se il
campo è rivolto verso il basso.
![]()
In questo modello si può pensare anche ad un elettrone (![]() ), legato al nucleo da una forza elastica con costante di
richiamo
), legato al nucleo da una forza elastica con costante di
richiamo ![]() . (
. (![]() )
)
Se il campo
elettrico varia sinusoidalmente nel tempo con pulsazione ![]() , l'equazione del moto dell'elettrone (
, l'equazione del moto dell'elettrone (![]() ) risulta:
) risulta:

![]()
![]()
![]() (*)
(*)
Si può pensare che l'elettrone oscilli con
frequenza uguale alla frequenza di ![]() applicato, cioè
applicato, cioè
![]()
Si ottiene:
![]()
![]()
sostituendo in (*):
![]()
![]()
da cui:
![]()
Il momento di dipolo ![]() risulta:
risulta:
![]()
ma il vettore ![]() polarizzazione (
polarizzazione (![]() numero di dipoli per unità di volume per il momento di
dipolo
numero di dipoli per unità di volume per il momento di
dipolo ![]() ) é stato posto proporzionale al campo
) é stato posto proporzionale al campo ![]() :
:
![]()
![]() = suscettività
elettrica
= suscettività
elettrica
per cui anche ![]() (momento di dipolo di
1 elettrone) é posto
(momento di dipolo di
1 elettrone) é posto ![]() :
:
![]() (8)
(8)
risulta sostituendo in ![]() :
:
![]()
da cui
![]()
![]() = polarizzabilitá
elettrica (9)
= polarizzabilitá
elettrica (9)
In definitiva:
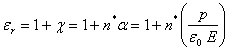
![]() (10)
(10)
Per ![]() (campo applicato costante
o nullo) l'elettrone vibra con la sua frequenza caratteristica
(campo applicato costante
o nullo) l'elettrone vibra con la sua frequenza caratteristica ![]() .
.
Applicando ![]() , se:
, se:
![]() "
"![]() " segue le oscillazioni di
" segue le oscillazioni di ![]() , lo spostamento ha lo stesso verso di
, lo spostamento ha lo stesso verso di ![]() , cioè in fase
, cioè in fase
![]() lo spostamento avviene in direzione opposta
alla forza
lo spostamento avviene in direzione opposta
alla forza ![]() e risulta sfasato di
180 gradi
e risulta sfasato di
180 gradi
L'espressione: 222d32c
![]() (11)
(11)
vale per 1 singolo
elettrone; di fatto ogni atomo (o molecola) possiede molti modi di oscillazione
con frequenze ![]()
![]() che sono le frequenze
caratteristiche a cui un atomo può assorbire ed emettere energia raggiante.
che sono le frequenze
caratteristiche a cui un atomo può assorbire ed emettere energia raggiante.
L'espressione di ![]() calcolato, diventa
calcolato, diventa ![]() per
per ![]() . Questo risultato non ha significato fisico. Infatti é stato
trascurato lo "smorzamento" nell'equazione del moto dell'elettrone. Tale
smorzamento é dovuto al fatto che l'elettrone irraggia energia, e ha
interazioni con gli atomi circostanti. Si deve introdurre un termine
proporzionale alla velocità.
. Questo risultato non ha significato fisico. Infatti é stato
trascurato lo "smorzamento" nell'equazione del moto dell'elettrone. Tale
smorzamento é dovuto al fatto che l'elettrone irraggia energia, e ha
interazioni con gli atomi circostanti. Si deve introdurre un termine
proporzionale alla velocità.
L'equazione del moto diventa :
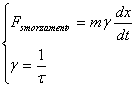
![]()
![]()
avendo fatto uso della grandezza complessa:
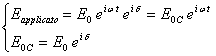
L'oscillazione dell'elettrone ha l'espressione: 222d32c
![]()
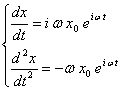
Per l'equazione del moto:
![]()
Da cui ricaviamo ![]() :
:
![]()
Dunque:
![]()
Ricordando che ![]() , ricalcolando
, ricalcolando ![]() si ottiene:
si ottiene:
![]() (11')
(11')
Ponendo ![]() e
e ![]() , e ricordando che:
, e ricordando che:
![]()
otteniamo:
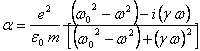 (12)
(12)
Ponendo
![]()
![]()
Ricordando che:
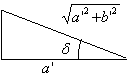
![]()
![]()
Risulta:
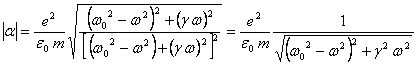
![]()
Da cui:
![]()
![]()
Segue le variazioni
del campo con un ritardo ![]() ; per
; per ![]() abbiamo
abbiamo ![]() = max ma non più
= max ma non più ![]() e
e ![]()
In definitiva la costante dielettrica complessa risulta per la (11'):
![]() (13)
(13)
Ponendo ![]() , detta pulsazione di plasma, dipende dal tipo di carica e
dalla densità, la parte reale ed immaginaria risultano rispettivamente:
, detta pulsazione di plasma, dipende dal tipo di carica e
dalla densità, la parte reale ed immaginaria risultano rispettivamente:
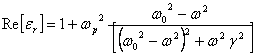 (14)
(14)
![]() (15)
(15)
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025