|
|
| |
Si fa uso della (6):
![]()
tale espressione fornisce la differenza di potenziale tra i punti A e B, non il potenziale in un punto. Per avere il potenziale in un punto, si può fare in modo da annullare il potenziale in B 737g64h .
Cioè la (6) è soddisfatta da V(x,y,z) +
cost. Si può scegliere la costante in
modo che ![]() = 0.
= 0.
Il campo vale:
![]()
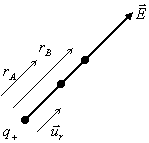
![]()
Si prende ![]() lungo il campo
lungo il campo ![]() . Pertanto
. Pertanto ![]() .
.
![]()
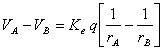
Cerchiamo adesso di annullare ![]() .
.
Per ![]() ,
, ![]()
Avendo posto ![]() risulta:
risulta: ![]()
In definitiva il potenziale di una carica
puntiforme rispetto all'![]() ove si è posto
ove si è posto![]() vale:
vale:
![]() (9)
(9)
Si intende per
dipolo elettrico il sistema formato da due cariche uguali e opposte ![]() e
e ![]() ad una distanza a.
ad una distanza a.
a)
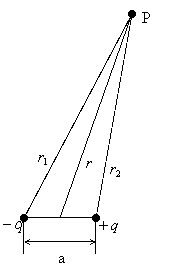 Calcoliamo il potenziale nel punto P.
Calcoliamo il potenziale nel punto P.
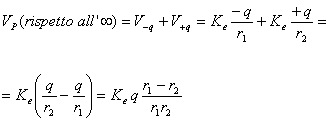
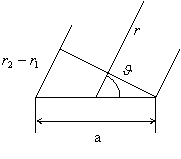 Se
Se ![]() si possono fare le
seguenti approssimazioni:
si possono fare le
seguenti approssimazioni:
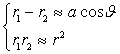
Per cui:
![]()
ove si è posto il momento di dipolo ![]() ;
;![]() con
con ![]() orientato dalla carica
(-) alla carica (+).
orientato dalla carica
(-) alla carica (+).
b)
Per determinare il campo ![]() , calcoliamo le componenti di
, calcoliamo le componenti di ![]() facendo uso di
facendo uso di ![]() . In questo
. In questo
caso il potenziale dipende da ![]() e pertanto si possono
ottenere le componenti radiale
e pertanto si possono
ottenere le componenti radiale ![]() e tangenziale
e tangenziale ![]() all'arco s (vedi fig.).
all'arco s (vedi fig.).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
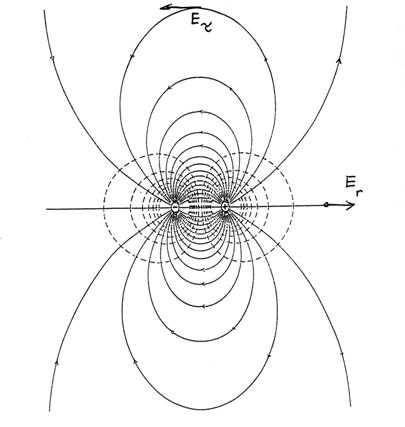
Le
linee di forza del campo ![]() di un dipolo
elettrico.
di un dipolo
elettrico.
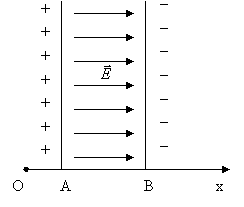
Un campo ![]() uniforme, cioè stesso
modulo,direzione e verso in tutti i punti, si vedrà in seguito che si realizza
tra due piastre metalliche parallele che portano cariche di segno opposto.
uniforme, cioè stesso
modulo,direzione e verso in tutti i punti, si vedrà in seguito che si realizza
tra due piastre metalliche parallele che portano cariche di segno opposto.
![]()
![]()
Vale il principio di sovrapposizione degli effetti:
![]() (somma di
"scalari")
(somma di
"scalari")
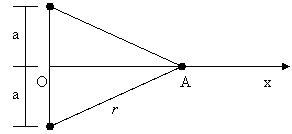
Consideriamo il caso di due cariche ![]() e
e ![]() poste simmetricamente
rispetto all'asse x.
poste simmetricamente
rispetto all'asse x.
![]() Poniamo:
Poniamo:
![]()
![]()
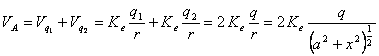
Facciamo ora alcune considerazioni:
![]() V nell'origine (x=0) risulta massimo
V nell'origine (x=0) risulta massimo
Facendo uso dell'espressione ![]() , poiché è V(x) si ottiene:
, poiché è V(x) si ottiene:
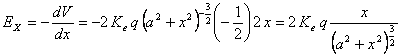
che coincide con il
risultato ottenuto sommando vettorialmente i campi ![]() delle due cariche. È
chiaro che ricavando
delle due cariche. È
chiaro che ricavando ![]() dal potenziale,
trattandosi di una funzione scalare, si semplificano i calcoli.
dal potenziale,
trattandosi di una funzione scalare, si semplificano i calcoli.
Andamento di ![]()
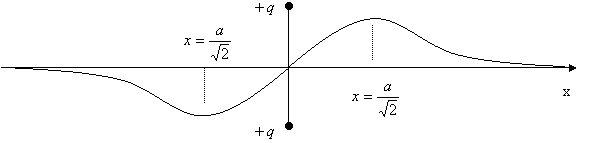
Andamento di V
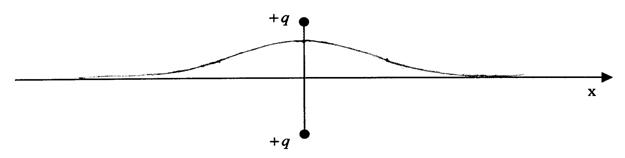
A massimi del potenziale corrisponde E = 0; a massimi del campo corrisponde flesso di V.
L'energia potenziale del sistema equivale al lavoro che si deve compiere dall'esterno per costruire il sistema.
Se le cariche sono
tutte positive, la repulsione coulombiana tende ad allontanarle. Per
avvicinarle si deve compiere un lavoro. Si pensi si portare tre cariche ![]() ,
, ![]() e
e ![]() una per volta dall'
una per volta dall'![]() fino ad occupare i vertici del triangolo
fino ad occupare i vertici del triangolo ![]() .
.
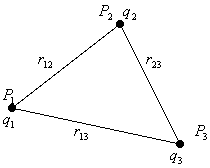
Porto
![]() dall'
dall'![]() in
in ![]()
![]() non ci sono cariche
non ci sono cariche
Porto
![]() dall'
dall'![]() in
in ![]()
![]() creato da
creato da ![]()
Porto
![]() dall'
dall'![]() in
in ![]()
![]() creato da
creato da ![]() e
e ![]()
![]()
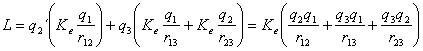
In generale:
![]() prendendo le
coppie di cariche una volta sola
prendendo le
coppie di cariche una volta sola
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026