- 848h73i 848h73i   Suoni (cd rom.)

Elaboratore: oggetto fisico. Posso rilevare

- 848h73i 848h73i   un flusso di corrente +/-

- 848h73i 848h73i   una q elettrica +/-

- 848h73i 848h73i   un raggio laser riflesso o meno da una superficie

- 848h73i 848h73i   una polarità magnetica nord o sud

- 848h73i 848h73i   ecc.

Tutte queste informazioni sono di tipo binario. Ciò vuol dire che abbiamo soltanto due alternative, 2 i valori ELEMENTARI che posso rappresentare all'interno dell'elaboratore.

Per convenzione i valori sono 0 e 1 (informazioni duali). Una delle 2 cifre si chiama bit (bynary digit).

0 1 2 informazioni (2¹).es: A, B.

00,01,10,11 4 informazioni con due stringhe da due (2²).es: A, B, C, D.

01000100 = BABA (ma è una convenzione)

10000100=CABA

000, 001, 010, 011, 100, 101, 110, 111 8 informazioni, es. 8 lettere 2³

Ogni volta si moltiplica per 2.se avessimo la stringa lunga 58 avremo 2⁵⁸

2ⁿ

n è la lunghezza della stringa

2 sono i simboli

CODIFICA CARATTERI

1) 848h73i   Scegliere lunghezza della stringa (non in maniera arbitraria.per esempio per 1000 caratteri una stringa da 5 non andrà bene).

2) 848h73i   Definire la convenzione che associa le stringhe ai simboli che voglio codificare.

Esigenza di avere degli standard, perché se io codifico qualcosa voglio che qualcuno riesca a decodificare ciò che ho fatto. Esistono dei codici standard.

- 848h73i 848h73i   ASCII (American Standard Code Information Interchange) : stringhe di 7 bit (2⁷)

- 848h73i 848h73i   ASCII ESTESO bit (2⁸).equivale a 256 caratteri

8 bit equivalgono ad 1 byte -> è l'unità di memorizzazione. Non troveremo mai i singoli bit.

- 848h73i 848h73i   UNICODE : 16 bit=2 byte= 2¹⁶ informazioni.per esempio è utile nella comunicazione fra civiltà diverse.vedi i caratteri cinesi.

CODIFICA NUMERI:

Come posso rappresentare il numero 27? Se giustapponessimo soltanto avremmo un problema di spazio.

Sistema Decimale giustapposizione di cifre ciascuna delle quali assume un ruolo a seconda della posizione

il primo 3 e l'ultimo hanno ruoli diversi perché occupano posizioni diverse

Sistema posizionale. Ogni cifra può assumere un valore tra 0 e 9. 10 è la base di calcolo.

Ora effettuo la stessa operazione ma in base 2

^{4 3 2 1 0}

0 + 2 + 8 + 64 + 256 = 330 con 9 bit

Per fare l'operazione inversa, ossia passare da un numero decimale ad un numero binario si divide sempre per due approssimando per difetto.nota bene che in un codice tipo 10101 l'ultima cifra è indicatrice se il numero è pari o dispari (in questo caso dispari.1 corrisponde a numero dispari, 0 a numero pari.).

Es:

330 848h73i 848h73i    

165 848h73i 848h73i    

82 848h73i 848h73i 848h73i    

41 848h73i 848h73i 848h73i    

20 848h73i 848h73i 848h73i    

10 848h73i 848h73i 848h73i    

5 848h73i 848h73i 848h73i 848h73i    

2 848h73i 848h73i 848h73i 848h73i    

1 848h73i 848h73i 848h73i 848h73i    

In tutto abbiamo difeso 9 volte.quindi riscriviamo la cifra considerando la colonna di dx dal basso verso l'alto

Es. (2):

binario decimale

N° Interni Naturali ( > o = di 0)

5 bit 2⁵ informazioni.tutti i numeri compresi tra 0 e 2⁵ - 1 (perché lo 0 già si considera.ricordati di questo perché spesso si sbaglia).

N° Interni Negativi

1) 848h73i   codifica il suo opposto in complemento 2

2) 848h73i   inverti ogni singolo bit della codifica

3) 848h73i   somma 1 a ciò che ottieni

Es: - 5

11 848h73i 848h73i 848h73i    

6 848h73i 848h73i 848h73i 848h73i    

3 848h73i 848h73i 848h73i 848h73i    

1 848h73i 848h73i 848h73i 848h73i    

Ricordiamoci ora che la prima cifra in una stringa di bit fornisce il segno , e piu' precisamente per convenzione useremo 0 per sottolineare che il numero è positivo, 1 se è negativo.

1 848h73i    

L'operazione inversa: passare da binario a decimale nel caso che il numero sia negativo (lo riconosco dal 1 all'inizio)

1) 848h73i   ignoro il primo bit

2) 848h73i   inverto i bit rimanenti

3) 848h73i   Decodifico e sommo 1 al risultato

RAPPRESENTAZIONE (codifica)

Di INFORMAZIONI

CARATTERI

NUMERI

INTERI + INTERI -

REALI con ,

CODIFICA DI UN NUMERO CON LA VIRGOLA

Per codificare un simile numero in sistema binario, ipotizzò che 3227, 815 sia uguale a 3.227.815 * 10³ (ho semplicemente riscritto il numero in modo da non avere piu virgole. La prima parte si definisce MANTISSA, la seconda ESPONENTE.

5 - 5

il secondo - 5 sarebbe in realtà 10^-5 ma noi riportiamo solamente l'esponente del numero 10, sia esso positivo o negativo, come in questo caso.

1000000 - 7

Se fossimo di fronte a 16 bit, sarebbero così distribuiti: i primi 10 andrebbero per la mantissa, i restanti 6 per l'esponente, ricordandoci però che la prima cifra della mantissa e la prima cifra dell'esponente (ovviamente calcolati nella stringa di bit) sono sempre riferiti al segno. Rimangono per il numero vero e proprio 9 cifre per la mantissa e 5 per l'esponente.

A 32 bit la struttura rimane immutata, 20 per la mantissa e 10 per l'esponente.il rapporto che lega i due è sempre di all'incirca 1:2.

Se l'esponente è negativo ci riferiamo ad un numero con virgola, se l'esponente è positivo stiamo parlando di un numero troppo grande.

Se fossimo di fronte a

7.289.315.815 848h73i 848h73i 848h73i 848h73i 848h73i 848h73i sono costretto a ricorrere ad una approssimazione e scrivere

nota che si potrebbe anche pensare di arrotondare e poi calcolare, ma si usa per convenzione il troncamento.

Possibili combinazioni

Mantissa / Esponente

+ M  / + E

+ M / - E

- M   / + E

- M   / - E

approssimazione (es. 3.247.100.829)

numero positivo con virgola

numero negativo troppo grande per essere rappresentabile come (1)

numero negativo con virgola

IMMAGINI

Ogni singolo quadratino viene chiamato pixel (picture element).

In questo caso la risoluzione è 11 * 8.

Il valore del bit codifica il colore.per convenzione per leggere l'immagine codificata si comincia dal quadratino in basso a sinistra e si continua andando a destra.In questo caso quindi dovremmo scrivere 11 bianchi, 11 bianchi, 2 bianchi , 6 neri, 2 bianchi ecc.

Per convenzione diciamo che

0 = bianco

1 = nero

In questo caso che la figura comincia a divenire piu' complessa avremo dei valori che saranno perfettamente o neri o bianchi.ma altri andranno approssimati con il colore dominante del pixel.se poi avremo che in un pixel la distribuzione dei colori è del 50% ciascuno, la nostra scelta sarà ininfluente, entrambi andranno bene.

Otterremo una figura del genere:

Per essere piu' precisi dovremo aumentare il numero di pixel.questa risoluzione viene definita GRADO DI PRECISIONE NELLA RAPPRESENTAZIONE IMMAGINE.si chiama altresì risoluzione. Eccone alcuni esempi comunemente usati nei monitor

Se ora voglio aggiungere dei colori alla mia immagine, per far si che non ci siano solamente bianco e nero, ma anche grigio chiaro e grigio scuro, serviranno 2 bit (2² informazioni).00, 01, 10, 11.

256 colori 8 bit

COMPRESSIONE: se in una immagine abbiamo per esempio il cielo, ci saranno moltissimi pixel azzurri.per comprimere l'immagine al posto che scrivere azzurro azzurro azzurro ecc.. per 24 volte scrivo 24 dove il numero mi dice il numero di pixel.se usassimo il primo metodo servirebbero 24 bit, cosi ne servono solo 2.

Un altro metodo e disegnare solo ¼ dei bit e poi fare la media fra i bit. Es:

Questo metodo fornirà immagini sfumate e non precise.se abbiamo un pixel bianco seguito a due pixel di distanza da uno nero, l'intermediario sarà grigio. Si ha sicuramente una perdita di informazione e pertanto questo metodo non va bene per le immagini precise. La griglia si chiama MATRICE.

L'approssimazione dell'immagine è sempre data da due fattori

APPROSSIMAZIONE

Finora si è parlato di IMMAGINI FISSE.passiamo ora a parlare di immagini in movimento

FILMATO:

Fotogrammi.il nostro occhio, con la frequenza di 24 fotogrammi/sec , percepisce un filmato. Codificare per noi adesso significa codificare le singole immagini.

--- --- --- ---

1foto

Esiste tuttavia il problema della compressione, perché i filmati contengono tantissime immagini.

1) 848h73i   MPEG. L'idea è di codificare la prima immagine e poi codifico solo le variazioni rispetto alla prima.c'è un intervallo di 11 fotogrammi, dopodichè si codifica di nuovo l'intera immagine perché si suppone che dopo 11 fotogrammi l'immagine sia cambiata notevolmente.

2) 848h73i   Elaboro la prima e la terza , e quella di mezzo è una media della due (così come era stato fatto per le immagini fisse).considero l'immagine di mezzo un enorme pixel.

Esercizio: un immagine con 256 colori occupa 8000 bit. Da quanti pixel è composta? Quanti bit occuperebbe se i colori fossero solo 128?

Per ogni pixel 8 bit 1000 pixel

1000 * 7 = 7000 bit

Osservazione: se raddoppio i pixel raddoppia lo spazio, se raddoppio i colori no.

Esercizio: Abbiamo una immagine di 30 * 30 pixel, a 256 colori.quanti bit occorrono?

900 pixel 8 / 7200

Si risparmia spazio dimezzando i pixel, non i colori!!

SUONO

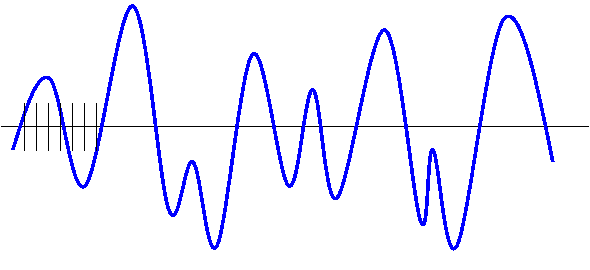
Gli intervalli di tempo si ripetono uguali e si chiamano CAMPIONI. Si valuta l'ampiezza d'onda.approssimazione.

La frequenza è data dai campioni / sec e si calcola in Hz. Maggiore è la frequenza e maggiore sarà la qualità del suono (come nelle immagini). I valori d'ampiezza d'onda dipende dai bit che posso utilizzare.

Lo spazio tenuto da un brano si calcola con n° campioni * bit di ogni campione.

Quanti campioni sono presenti = secondi * frequenza.