(x - x0)² + (y - y0)² = r² equazione della circonferenza di centro C(x0; y0) e di raggio r.

x² + y² = r²   equazione della circonferenza di centro O(0; 0) e di raggio r.

x² + y² + ax + by + g equazione canonica della circonferenza; equazione di 2° grado in x e y, mancante del termine contenente il prodotto xy e con i coefficienti di x² e y² uguali a 1.

La PARABOLA è il luogo geometrico dei punti di un piano equidistanti da un punto fisso F (detto fuoco) e da una retta data d (detta direttrice).

P(x,y)€g n d(P,F)=d(P,d)   d(F,d)=2m delta=0

y = ax² equazione della parabola di vertice l’origine O e asse di simmetria coincidente con l’asse y.

a>0  concavità verso l’alto

a<0  concavità verso il basso

vertice O(0,0)

asse di simmetria  s: x=0 (asse y)  

y - y0 = a(x - x0)² equazione della parabola con asse di simmetria parallelo all’asse y e vertice in V(x0 ;y0).

y = ax² + bx + c equazione della parabola con asse di simmetria parallelo all’asse y

a>0  concavità verso l’alto

a<0  concavità verso il basso

vertice  V(-b/2a;-delta/4a)

assi di simmetria    s1: x=-b/2a  s2: y=-b/2a

x = ay² + by + c equazione della parabola con asse di simmetria parallelo all’asse x.

a>0  concavità verso destra

a<0 concavità verso sinistra

vertice  V(-delta/4a;-b/2a)

asse di simmetria   s: y=-b/2a

L’ELLISSE è il luogo dei punti di un piano per i quali è costante la somma delle distanze da due punti fissi detti fuochi.

P€g nF1P+F2P=2a a>0 F1F2=2c F1(-c; 0) F2(c; 0) P(x; y) delta<0

(x² / a²) + (y² / b²) = 1 equazione dell’ellisse riferita al centro e agli assi di simmetria, cioè simmetrica rispetto agli assi x e y e all’origine O(0 ;0) con i fuochi sull’asse x.

(x² / b²) + (y² / a²) = 1 equazione dell’ellisse riferita al centro e agli assi di simmetria, cioè simmetrica rispetto agli assi x e y e all’origine O(0 ;0) con i fuochi sull’asse y.

((x - x0)² / a²) + (y - y0)² / b²) = 1 equazione dell’ellisse riferita a delle parallele ai suoi assi di simmetria di centro (x0;y0) e di semiassi a e b

mx² + ny² + px + qy + r = 0   m•n>0 equazione dell’ellisse riferita a delle parallele ai suoi assi di simmetria; equazione di 2° grado in x e y, mancante del termine contenente il prodotto xy e con i coefficienti di x² e y² concordi (m•n>0).

L’IPERBOLE è il luogo dei punti del piano per i quali è costante la differenza delle distanze tra due punti fissi detti fuochi

P€gn|PF2-PF1|=2a a>0 F2F1=2c F(±sqrt(a²+ b²)) delta>0

(1) (x² / a²) - (y² / b²) = 1   equazione dell’iperbole riferita al centro e agli assi di simmetria cioè simmetrica rispetto ad essi. Ponendo a sistema l’equazione y=0 dell’asse x con la (1) si ottiene x = ±a, l’asse x interseca quindi l’iperbole nei punti A1(a; 0) e A2(0; a) chiamati vertici dell’iperbole. Gli asintoti dell’iperbole sono rette che non intersecano mai l’iperbole, ma ad essa si avvicinano indefinitamente a mano a mano che ci si allontana dall’origine ed hanno queste equazioni y =(b/a)x e y=-(b/a)x; l’equazione complessiva degli asintoti è (x²/a²)-(y²/b²)=0

mx² + ny² + px + qy + r = 0    m•n<0 equazione dell’iperbole con assi di simmetria paralleli agli assi coordinati; equazione di 2° grado in x e y, mancante del termine contenente il prodotto xy e con i coefficienti di x² e y² discordi (m•n<0).

((x - x0)² / a²) - (y- y0)² / b²) = ± 1 equazione dell’iperbole con assi di simmetria paralleli agli assi coordinati e centro O(0 ; 0); l’equazione complessiva degli asintoti è y-y0=±b/a(x-x0).

GONOMETRIA

L’ ampiezza di un arco è l’ampiezza dell’angolo al centro corrispondente.

Il grado è la 360ª parte della circonferenza usata come unità di misura.

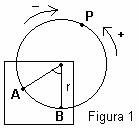
Il radiante è l’arco che rettificato è uguale al raggio della circonferenza alla quale l’arco appartiene (fig.1).

Il campo di esistenza è l’insieme di tutti quei numeri reali per cui esiste la funzione ed è reale.

La circonferenza goniometrica è la circonferenza avente il centro nell’origine degli assi e il raggio = 1.

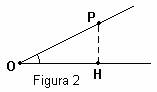
Il seno di un angolo è il rapporto tra la distanza di un punto P, del secondo lato, dalla retta del primo e la distanza dello stesso punto dal vertice O (fig.2); nella circonferenza goniometrica è l’ordinata di P; il suo campo di esistenza varia da - a + il condominio da –1 a 1.

Il coseno di un angolo è il rapporto tra la proiezione , sulla retta del primo lato, di un segmento OP scelto sul secondo e il segmento OP stesso; nella circonferenza goniometrica è l’ascissa di P (fig.2).

La tangente di un angolo è il rapporto tra la distanza di un punto P, sul secondo lato, dalla retta del primo e la proiezione, sempre sulla retta del primo lato, del segmento OP scelto sul secondo (fig.2); negli archi di 90° e 270° non è definita la tangente.

sena = HP/OP    cosa=OH/OP tga=HP/OH

coseca=OP/HP  seca=OP/OH cotga=OH/HP

Un’equazione goniometrica è un’equazione in cui figurano funzioni goniometriche, cioè quando la x compare nell’argomento della funzione goniometrica.   Es. senx=1/2

Prima relazione fondamentale: cos²a + sen²a