I momenti - Momento di primo ordine

es. x = 2, 3 y = 10, 20 (x_i+y_i) = (2+3) + (10+20)

Le proprietà sommatorie valgono solo per le somme.

Se io faccio la sommatoria di una costante è come se moltiplicassi la costante per n.

m = n. m

La media aritmetica è uguale a /N

Si può avere una distribuzione normale con delle forme abbastanza dirette.

Problema: trovare il parametro di dispersione o di variabilità momenti.

Momento di primo ordine

e_i = x_i - m

errore statistico; può essere >,< o = a zero.

Ricorrendo all'errore statistico si può vedere quale è l'errore medio.

M1 = e_i

n

Problema: la somma degli errori fa zero, quindi noi non possiamo usare questo metodo come misura di variabilità. Usiamo, quindi, il.

Momento di secondo ordine

M2 = s (ei)²

n .

Eleviamo al quadrato perché così tutti i valori diventano positivi e, quindi, la somma non farà più zero.

s s

Momento di terzo ordine

M3 = (ei)³

n .

Può essere + o - perché è un cubo, ma non è necessariamente = a zero.

Momento di quarto ordine

M3 = (ei)⁴

n .

Indice di asimmetria o schiacciamento

Noi possiamo calcolare un indice che si chiama asimmetria o schiacciamento che mi dice quanto la distribuzione dei dati che ho è unimodale.

S = M3

M2 . M2

E' - se gli scarti negativi son più grandi di quelli positivi.

Es. 2, 2, 2, 6 M1 = -1-1-1+3 = 0 M3 = -1-1-1+27 = 24

Se io ho tanti dati piccoli spostati a sx. e pochi dati grandi spostati a dx. avrò un M3 positivo.

Es. A m_A M3_A = +

B -2, 7, 9, 10 m_B scarti

Se io ho pochi numeri grandi positivi e tanti numeri piccoli negativi M3 +

schiacciamento a dx.

Se io ho tanti numeri grandi negativi e pochi numeri piccoli positivi M3 -

schiacciamento a sx.

S = M3 = >0  schiacciamento a dx.

M2 . M2 <0 schiacciamento a sx.

Kurtosi

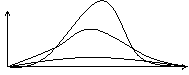Le distribuzioni normali possono essere:

leptocurtiche

normocurtiche

platocurtiche

Se i cubi dei numeri grandi tendono a soverchiare i cubi dei numeri piccoli, ciò tende ancor di più nella quarta.

K = M4

M2 . M2

Se:

K >3 distribuzione     leptocurtica

K < 3 " platocurtica

K = 3 " normocurtica

Calcola m, Mod, Med, S e K

dati: 1, 1, 2, 2, 2, 3, 3, 4, 10, 12

dati: 0, 1, 9, 9, 10, 10, 11, 11

Problemi di probabilità

Tratte a caso due carte da un mazzo, qual'è la probabilità che escano due cuori, oppure che la prima sia >5 e la seconda sia un A di quadri.

Tratte tre carte da un mazzo, qual'è la probabilità che la somma della seconda più la terza faccia cinque, oppure che la prima sia un K di quadri.

Problemi di permutazioni

Abbiamo 6 libri, di cui 2 indivisibili. Volendo disporli su uno scaffale circolare (senza inizio) in quanti modi posso disporli dato che voglio che tra i due libri indistinguibili ve ne sia sempre interposto un altro?

Espansioni binomiali

Pierino ama lanciare vasi di fiori sui passanti. Mercoledì ha tirato 12 vasi ed ha colpito 11 passanti. Alla mamma che lo ha brontolato Pierino ha replicato che non l'aveva fatto apposta e che stava tirando a caso. Possiamo affermare che Pierino ha mentito

2) Sapendo che su 22 idraulici 12 picchiano la moglie e che su 11 avvocati 10 picchiano la moglie, qual'è la probabilità di picchiare la moglie se si è idraulici o avvocati?