|
|
| |
Quando il valore unitario di una particella non è uniforme, il parametro oggetto della suddivisione non è l'area, ma il corrispondente valore totale. Questa particolare divisione avviene quando il notaio o lo stesso proprietario decidono di dividere una particella di terreno in parti che abbiano lo stesso valore unitario.
Dal punto di vista estimativo è un 424e44e operazione che prende il nome di frazionamento. Esso si rende necessario quando il trasferimento di proprietà o di un altro diritto reale riguarda solo una parte delle particella.
Il frazionamento individua le nuove linee di
confine e determina le superfici e i redditi imponibili delle particelle
derivate, con effetto giuridico e catastale. Per effettuare il frazionamento il
tecnico deve per prima cosa accertare i dati tecnici della particella su di un
estratto di mappa; l'estratto di mappa ed i relativi atti censuari devono
essere riportati dal professionista sull'apposito modello
I punti fiduciali devono individuare un triangolo che racchiuda per intero la particella da frazionare. Se la paricella esce dai limiti consentiti occorrono altri punti di appoggio che individuino una serie di triangoli consecutivi costituenti una maglia sfiduciale.
È consigliato che il progettista effettui un rilievo planimetrico per controllare la corrispondenza con la mappa, per accertare l'esistenza di termini di proprietà e per individuare la natura e la posizione dei punti fiduciali. Le operazioni di rilievo devone essere eseguite rispettando diverse regole:
Le misure angolari devono essere espresse in gradi centesimali;
Le distanze lineari devono essere ricondotte all'orizzonte ed espresse in metri;
Gli angoli dei triangoli fiduciali non devono essere inferiori a 30° centesimali;
Le stazioni celerimetriche poste all'esterno del triangolo fiduciale non devono distare dal lato rispetto al quale sporgono per più del 30% della distanza medesima.
Dopo aver compilato il libretto delle misure il progettista, deve passare all'elaborazione dei dati con un programma chiamato PREGEO, che elabora i dati inseriti restituendo direttamente il disegno dei punti battuti.
Gli elaborati tecnici che deve presentare sono:
Il modello 51 è un foglio in carta lucida che contiene l'elaborato grafico dell'oggetto del rilievo e il risultato del frazionamento, cioè il disegno della particella frazionata con le nuove linee dividenti e le lettere di identificazione delle particelle frazionate;
Il modello 51 FTP è un documento cartaceo contenente in triplice copia a ricalco la dimostrazione numerica del frazionamento, cioè il risultato della ripartizione numerica fra le particelle derivate della superficie e dei redditi delle particelle originarie;
Lo schema del rilievo è la dimostrazione grafica di come è avvenuto il frazionamento, redatto in scala opportuna, riportante lo schema delle operazioni di rilievo; nel disegno compaiono i P.F.utilizzati, le stazioni utilizzate per il rilievo, l'oggetto del rilievo con la numerazione dei punti di dettaglio ed eventuali misure integrative;
Il libretto delle misure è un elaborato che contiene l'illustrazione del rilievo fatto: metodo utilizzato, strumentazione impiegata, stazioni, punti osservati.
Il modello censuario contiene la documentazione informatica corrispondente a quella presentata in forma grafica con il modello 51 FTP, e serve per l'aggioranmento automatico dei dati censuari;
La relazione tecnica è un allegato che raccoglie tutte le osservazioni del tecnico e le giustificazioni del suo operato;
Il floppy disk contiene i dati del programma PREGEO, oltre alle distanze riportate nel libretto delle misure e quelle riportate nel modello 51 FTP.
Gli elaborati del tipo di frazionamento vanno presentati ad un apposito sportello dell'Ufficio provinciale dell' Agenzia del territorio . le informazioni metriche e censuarie contenute negli elaborati vengono analizzate tramite computer per il controllo della loro certezza.
Ora analizziamo la procedura analitica della divisione delle aree a diverso valore unitario:
Nel caso di dividente uscente da un vertice:
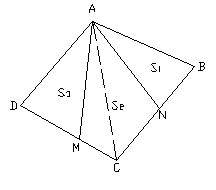
La prima cosa da fare è individuare l'area S1 facendo il rapporto tra il valore da staccare V1 ed il suo valore unitario U1:
S1 = ![]()
In seguito con la formula inversa dell'area
si trova il lato ![]() :
:
![]() =
= ![]()
Allo stesso modo si risolve il triangolo ADM.
Un altro caso di dividente uscente da un vertice si ha quando si deve dividere la particella in due sole parti:
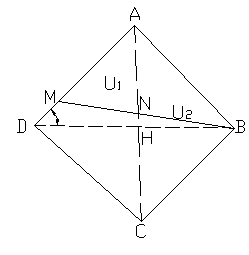
Si procede utilizzando la linea di prova che ci permette di trovare la posizione della dividente:
VABD = AABH x U1 + AADH x U2
V1 = V2 = ![]()
V1 < VABD
In questo modo si è raggiunto un valore
superiore a quello cercato e si può procedere al calcolo dell'angolo ![]() d'inclinazione della
dividente:
d'inclinazione della
dividente:
V* = VABD - V
V* = ABHN x U1 + ADMNH x U2
V* = ABHN x U1 + (ABAM - ABHN x U2
V* = ABNH x (U1-U2) + ABDM x U2
V* = 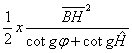 x (U1 - U2) +
x (U1 - U2) + 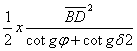 x U2
x U2
2xV*x[cotg²φ + cotg φ x (cotg δ2 + cotg H)
+ cotg δ2 x cotg H] =![]() x (cotg φ + cotg δ2) x (U1 - U2) +
x (cotg φ + cotg δ2) x (U1 - U2) + ![]() x (cotg φ + cotg H) x U2
x (cotg φ + cotg H) x U2
cotg²φ x [2xV*] + cotg φ [2xV* x (cotg δ2
+ cotg H) - ![]() x (U1 - U2) -
x (U1 - U2) - ![]() x U2] + [2xV*x cotg
δ2 x cotg H -
x U2] + [2xV*x cotg
δ2 x cotg H -![]() x cotg δ2 x (U1 - U2) -
x cotg δ2 x (U1 - U2) - ![]() x cotg H x U2] = 0
x cotg H x U2] = 0
Ora si risolve l'equazione di secondo grado ricavando e per finire si verificano i valori delle aree, dopo aver risolto i triangoli intervenuti nell'equazione:
VABM = VBCDM
Con una dividente parallela:
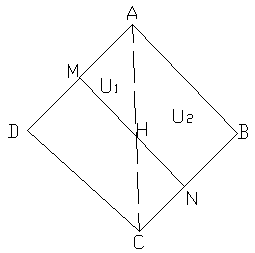
Si utilizza il problema del trapezio per quantificare l'altezza h da "staccare":
V* = AAHM x U1 + AABNH x U2
V* = (AABNM - AABNH) x U1 + AABNH x U2
V* = AABNM x U1 + AABNH x (U2 - U1)
V* = ![]() x [
x [![]()
![]() -h (cotg +cotg )] x h x U1 +
-h (cotg +cotg )] x h x U1 +![]() x [
x [![]()
![]() -h (cotg 2+cotg )] x h x (U2 - U1)
-h (cotg 2+cotg )] x h x (U2 - U1)
2x V*= [![]()
![]() -h (cotg +cotg )] x h x U1
+ [
-h (cotg +cotg )] x h x U1
+ [![]()
![]() -h (cotg 2+cotg )] x h x (U2
- U1)
-h (cotg 2+cotg )] x h x (U2
- U1)
h²x [cotg x U1 + cotg x U1 + cotg 2 x (U2 - U1) + cotg x (U2 - U1)]
+ h x [2x![]() X U1] + [2 x V*]= 0
X U1] + [2 x V*]= 0
Dopo aver ricavato h, dall'equazione di secondo grado, si calcolano:
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]()
![]() -h (cotg +cotg
-h (cotg +cotg
Infine si verifica il valore del terreno V1:
V1 = AAML x U1 + AABNL x U2
Staccante superficie nota con una curva:
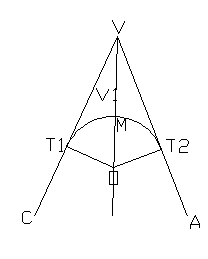
L'area del settore circolare da "staccare" vale:
V* = ![]() R
R![]() tang
tang![]() U1 +
U1 + ![]() R
R![]() tang
tang![]() U2 -
U2 - ![]()
![]() R
R![]()
![]() radU1-
radU1-![]()
![]() R
R![]()
![]() radU2
radU2
V* = ![]() (tang
(tang![]() )(U1 + U2) -
)(U1 + U2) - ![]() (
(![]() rad)(U1 + U2)
rad)(U1 + U2)
R = 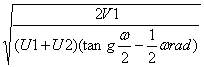
In questo modo si determina il raggio della curva staccante la superficie nota.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025