|
|
| |
ISTITUTO TECNICO INDUSTRIALE STATALE
"ALESSANDRO ROSSI"
LABORATORIO DI TECNOLOGIA
Relazione di Tecnologia
Taratura di un Calibro a Corsoio
Valutazione:
1. OGGETTO :
Eseguire la taratura del calibro a corsoio a nonio cinquantesimale.
2. INTRODUZIONE : NOZIONI TEORICHE
Il calibro a corsoio è lo strumento di misura più largamente utilizzato nelle officine meccaniche per misurazioni relativamente precise.
La storia della strumentazione dimensionale ha inizio con l'invenzione dei nonio intuito dal portoghese Pedro Nunes, che nel 1542 pubblicò la descrizione di un ingegnoso sistema per misurare picc 131h72b oli archi con sufficiente precisione. Al tedesco Ciavius (1604) si deve il perfezionamento dei nonio, e al francese Pierre Vernier (1631) da cui è derivato il nome «verniero», si deve l'attuale forma dei calibro a corsoio.
Esso è adoperato per effettuare misurazioni con approssimazione di frazione di millesimo. Il calibro è formato da un'asta che da una parte è millimetrata, e dall'altra è divisa in pollici e sedicesimi di pollice. Inoltre presenta due beccucci B per misurazioni esterne, due beccucci B' per misurazioni interne ed una linguetta L per misurazioni di profondità.
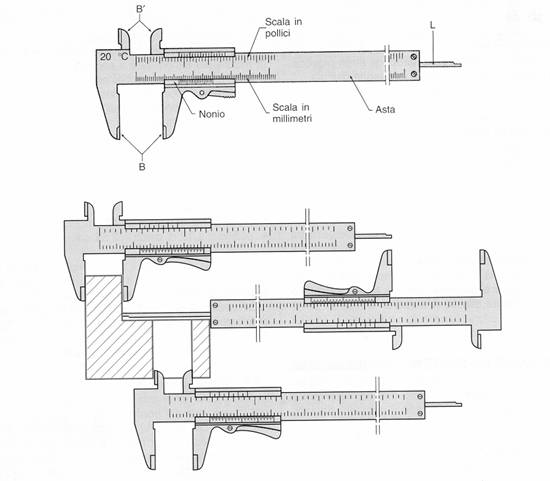
Con il calibro si ottengono approssimazioni di un decimo, un ventesimo e un cinquantesimo di millimetro, mediante il dispositivo dei nonio, o verniero. Il nonio è un'asta mobile, scorrevole sull'asta fissa graduata in millimetri; la lunghezza del nonio è divisa in n parti uguali che corrispondono alla lunghezza di n - 1 parti dell'asta fissa. Ogni divisione dei nonio ha quindi una lunghezza pari al rapporto (n - l)/n. Per esempio nel calibro decimale ogni divisione dei nonio risulta essere pari a (10 - 1)/10 = 9/10 di millimetro. Questa lunghezza risulta più piccola di quella dell'asta fissa di una quantità k, detta approssimazione dei nonio. Infatti:
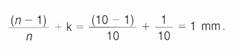
Si hanno tre tipi di nonio:
a) nonio decimale: su
una lunghezza di
b) nonio ventesimale: su
una lunghezza di
e) nonio cínquantesimale: su
una lunghezza di
Ci sono calibri più precisi ma il grado di difficoltà di lettura e il tempo ne sconsigliano l'utilizzo.
Per misurazioni di precisione utilizziamo il micrometro.
Nella lettura dello strumento possono presentarsi tre diversi casi:
l. Il tratto dei nonio segnato con zero è allineato con un tratto
dell'asta fissa millimetrata. Questo tratto individua in millimetri la misura
che risulta essere un numero intero; in figura 1 si leggono
2. Il tratto dei nonio segnato con zero cade nell'intervallo tra due tratti
dell'asta fissa millimetrata: la misura risulta formata dal numero intero in
millimetri corrispondente al tratto dell'asta fissa immediatamente a sinistra
dello zero dei nonio (fig. 2). Si individua poi quale tratto dei nonio è
allineato con un tratto dell'asta fissa. In figura 2, che rappresenta un nonio
decimale, al tratto dell'asta fissa corrisponde il numero 9 dei nonio e la
misura risulta essere:
Nessun tratto dei nonio
è allineato con un tratto dell'asta fissa, ma si hanno due tratti dei nonio
compresi fra due tratti dell'asta fissa. In figura 3 sono così disposti: il
tratto 5, indicato con n, e il
6 con n + l. Si possono
eseguire due letture, entrambe inesatte, perché se si considerano coincidenti i
due tratti a sinistra (5 dei nonio e 9 della scala fissa), si ha una lettura
per difetto; se si considerano invece coincidenti i due tratti a destra (6 dei
nonio e 10 della scala fissa) si ha una lettura per eccesso. La misura reale è
quella compresa tra le due letture. Con questo terzo caso si introduce il
concetto di approssimazione, che
può essere definita come la differenza tra
la misura in eccesso e quella in difetto; nel
nostro esempio questa è pari a 1/10 di millimetro =


Figura 1 Figura 2
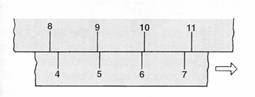
Figura 3
I calibri a nonio maggiormente usati sono quelli ventesimali (fig. 1.3), il cui nonio ha una lunghezza di diciannove millimetri con venti divisioni, o cinquantesimali (fig. 1.9), il cui nonio misura quarantanove millimetri ed è diviso in cinquanta parti.
Per evitare errori di lettura dovuti alla difficoltà di individuare la
coincidenza della tacca dei nonio con una tacca della scala fissa, si è
realizzato il calibro a orologio (fig. 1.10), in cui il beccuccio mobile indica
la parte intera della lettura, con scansione in multipli di
Ancora più pratici e
immediati sono i calibri à corsoio con visualizzatore a cristalli liquidi.

Calibro Cinquantesimale

Calibro a orologio
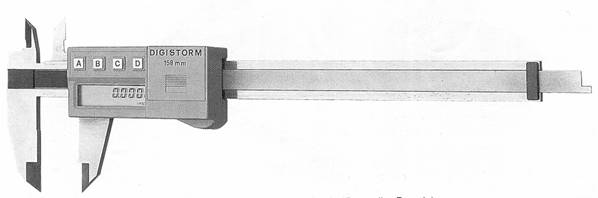
Calibro con visualizzatore a cristalli liquidi
Bisogna specificare poi, che i calibri, se ricavati da pezzi stampati, risultano molto più robusti e sono in grado di conservare meglio l'inalterabilità della loro precisione.
Le fibre dell'acciaio di cui sono composti, seguono l'andamento geometrico del pezzo. L'andamento delle fibre d'acciaio presenti sulle bocche di misurazione e sull'asta del calibro, vengono ricavate dai pezzi stampati. In questo modo la struttura del calibro risulta molto rinforzata e, in particolare, diviene più resistente alle deformazioni e alle rotture.
Se invece ricaviamo il calibro da un processo di tranciatura di lamiere, l'andamento delle fibre d'acciaio è differente: difatti le fibre risultano interrotte e non seguono l'andamento geometrico del pezzo.
3. APPARECCHIATURA UTILIZZATA
La nostra apparecchiatura, utile per il corretto svolgimento dell'esperienza, era composta da un semplice calibro a corsoio a nonio cinquantesimale a bloccaggio automatico (con portata pari a 157,90mm e sensibilità approssimata 0,05mm) simile al calibro della figura precedente.
Abbiamo poi tarato lo strumento servendoci di alcuni blocchetti pianoparalleli di riscontro di serie 1 (adatti per l'appunto a tarature di strumenti di misura) che avevano una classe di precisione pari a 1 (secondo la normativa UNI ISO 3650) chiamati blocchetti Jhonson.
Utilizzavamo inoltre dei guanti di lattice e delle pinze di legno per il motivo che non dovevamo toccare i blocchetti con le mani poiché il nostro calore avrebbe potuto causare una dilatazione termica che avrebbe influito successivamente sulla condotta della prova. Prima di effettuare la misurazione con il calibro, pulivamo i blocchetti utilizzando della benzina Avio e aiutandoci con un pennellino. Una volta svolta l'operazione di misura, ricoprivamo nuovamente i blocchetti con del grasso di vaselina per poi riporli nel loro apposito contenitore. Abbiamo condotto la prova su di un piano di lavoro, o piano d'appoggio, indeformabile poiché costruito in granito.
4. CONDOTTA DELLA PROVA
Abbiamo incominciato la prova munendoci di guanti, pinze di legno e blocchetti Jhonson. Ci hanno consegnato poi il calibro che dovevamo tarare e noi, abbiamo deciso di dividere la portata in 3 parti, sia per comodità, sia perché, agendo in questo modo, otteniamo 3 misure per ogni divisione e possiamo perciò ottenere valori molto più precisi di valore medio, cioè che si avvicinano maggiormente al valore di lettura campione. Abbiamo occupato i nostri posti di lavoro e ci siamo divisi i compiti. Per essere sicuri dell'attendibilità dello strumento, abbiamo verificato a inizio prova, che la tacchetta relativa allo 0 della scala in millimetri del calibro, corrispondesse esattamente allo 0 della scala graduata del nonio. Una volta che il pezzo era stato prelevato dal contenitore e pulito dal grasso di vaselina grazie alla benzina Avio, veniva passato nelle mani dell'operatore il quale, con precisione, doveva effettuare la misura del blocchetto Jhonson, ripetendola per 3 volte. Ogni qual volta rilevava una misura la dettava ad un alto incaricato di prendere nota di tutti i valori letti dall'operatore durante l'esperienza. Bisogna ricordare anche che noi ci riferiamo alle normative UNI e perciò specifichiamo che l'esperienza è stata svolta in un luogo chiuso che presentava una temperatura di 22° e ad una pressione pari a quella atmosferica normale. Noi abbiamo inoltre scelto di effettuare solo 9 misurazioni relative a 9 blocchetti Jhonson scelti arbitrariamente e così, in seguito, siamo riusciti a costruire una tabella (riportata di seguito al punto 5. DATI DELLA PROVA) che riassume tutti i valori letti, quelli campione,e anche i valori medi nonché gli errori percentuali e relativi riscontrati durante la prova.
5. DATI DELLA PROVA, ELABORAZIONE DATI E TABELLE
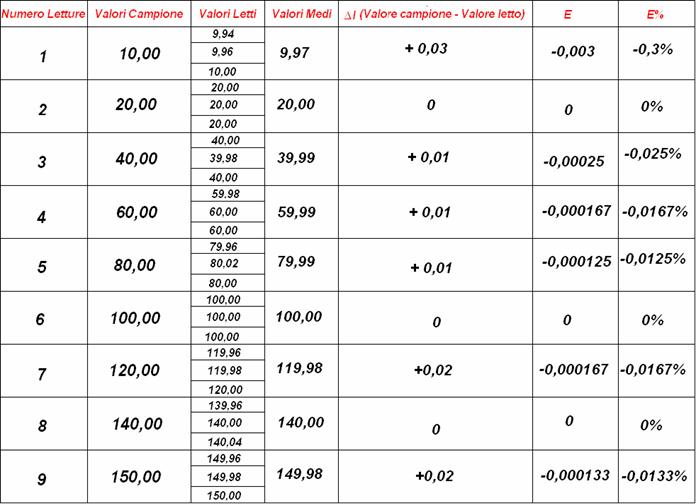
Nella tabella sono riportati tutti i valori ottenuti durante lo svolgimento dell'esperienza, più alcuni dati che sono frutto di formule algebriche utili ad ottenere:
La ∆l che corrisponde a:
![]()
L'E, che corrisponde all'errore relativo, e si può facilmente ricavare dalla formula:

Mentre
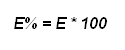
Mentre per ricavare analiticamente il valore medio, sommavamo i tre valori ottenuti e poi li dividevamo per il loro numero, cioè tre:
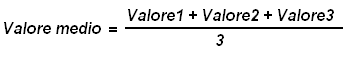
6. CONCLUSIONI
Osservando i dati raccolti nella tabella, posso affermare che l'esperienza è stata svolta con successo poiché non sono stati riscontrati errori notevoli che avrebbero potuto compromettere l'esito. Le imprecisioni di cui parlo possono essere causati da una poca attenzione dell'operatore che, non leggendo correttamente i valori sul calibro, causa un tipico errore di parallasse. Ma molti sbagli, comunque, possono essere compiuti anche dallo stesso strumento di misura. Per osservare e commentare meglio l'errore che abbiamo commesso, ho ritenuto opportuno costruire un grafico il quale presenta nelle ordinate i valori veri dati dai blocchetti Jhonson, mentre nelle ascisse sono presenti i valori da noi ottenuti grazie alle misurazioni. Inoltre vi è una retta contraddistinta dal colore blu, che rappresenta la retta ideale, cioè la retta che avremmo dovuto ottenere se non avessimo commesso nessun tipo di errore. Paragonando perciò le due curve possiamo notare che la nostra non si distanzia di molto da quella ideale. Concludo così ribadendo che l'esperienza è stata conclusa con successo poiché non è stato riscontrato un errore notevolmente grande e quindi il calibro a corsoio a nonio cinquantesimale utilizzato, è stato correttamente tarato.

|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025