CALCOLO DELLE PERDITE DI CARICO ALL' INTERNO DI UNA TUBAZIONE

meccanica

ITIS "ENEA MATTEI" SONDRIO	Laboratorio Di Meccanica & Macchine		Esercitazione N° 3
Tema Dell'Esercitazione: CALCOLO DELLE PERDITE DI CARICO ALL' INTERNO DI UNA TUBAZIONE
Schema Dell'Esercitazione: P.V.   z   y=9cm (da tabella)

 

P.O.

PV = Livello dell'acqua nella vasca piezometrica

PO = N° 6 curve a 90° di raggio 6,5 cm lunghezza effettiva dei tubi == 60 cm

Livello d'acqua nei tubi :

1. 52 cm
2. 40 cm
3. 20 cm

IDRODINAMICA

L'idrodinamica studia il moto dei liquidi. Si supponga una massa liquida che si muove entro un

conduttore: quando una particella si sposta dalla posizione occupata al suo posto subentra subito

quella che la segue, per cui la traiettoria descritta risulta materializzata da una successione continua

di particelle che costituiscono un filetto fluido. Un fascio di filetti costituisce una corrente. Sezione

trasversale di una corrente è la superficie che taglia perpendicolarmente tutti i filetti liquidi:quando

i filetti sono paralleli la sezione risulterà piana.

La portata è il volume di liquido che attraversa una data sezione nell'unità di tempo. I liquidi

perfetti, ossia senza viscosità, non risentono durante il moto di resistenze di attrito alloro interno e

alle pareti con le quali si trovano in contatto.

L'acqua è un liquido reale 545g66f anche se non risente di elevate resistenze durante il moto; essa si

comporta in modo prossimo a quello di un liquido perfetto: tutte le volte che, come appunto nel

caso dell'acqua, si possono ritenere piccole le resistenze di attrito, i liquidi si considerano come

perfetti salvo poi tenere conto della semplificazione fatta con opportuni coefficienti correttivi

sperimentali.

Un'altra classificazione del moto tiene conto delle resistenze. Si chiama lento o laminare, o di

Poiseuille, il moto di un liquido in cui le resistenze sono proporzionali alla velocità: 't =ocVcon 't

Resistenza specifica riportata ad unità di superficie di contatto fra liquido e parete (si verifica quando

le velocità sono molto piccole come nei mezzi filtranti delle falde acquifere sotterranee).

Si chiama turbolento o di Venturi, il moto di un liquido in cui le resistenze variano col quadrato

della velocità ('t J3V2)ed i cui i valori puntuali di velocità oscillano intorno ad un valore medio:

questo ultimo è il caso più comune di moto.

La distinzione tra questi due tipi di moto è legata al numero di Reynolds (Re)della corrente.

LE PERDITE DI CARICO

Il concetto di perdita di carico è intuitivo : se applico una certa pressione ad un fluido che fuoriesce da un tubo, la portata sarà maggiore in un tubo di grande diametro rispetto a quella di un diametro più piccolo. E sarà maggiore in un tubo liscio rispetto ad un tubo rugoso; e così via. In un canale perfettamente orizzontale, ad esempio, l'acqua si disporrà con un livello decrescente dal punto di alimentazione a quello di efflusso : la differenza di livello è appunto la perdita di carico nel canale alla portata che passa in esso.

PERDITE DI CARICO DISTRIBUITE

Prenderemo qui in esame il metodo utilizzato per calcolare una nuova grandezza R,detta perdita di carico;ossia l'energia dissipata per unità di tempo e di portata che risulta essere pari alla differenza di pressione diviso la densità del fluido.

(1)

Per praticità tali perdite vengono classificate in perdite di carico distribuite (Rdis) e concentrate (Rconc).

Per capire meglio prenderemo ad esempio un tubo cilindrico,retto e uniforme nel quale scorre un fluido.

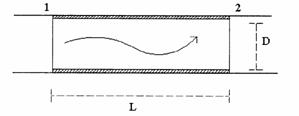
Consideriamo ora la sezione 1-2 ove non sono presenti impedimenti (quali rubinetti e valvole) e per la quale varrà ancora l'equazione (1).

Se la dissipazione dell'energia dipende dal numero di Reynolds,dalla lunghezza del tubo e non dalla variazione delle sezioni attraverso cui passa il fluido,è indicata con il nome di perdita di carico distribuita.

Per capire al meglio la logica di base,è necessario fare un piccolo passo indietro nel mondo della fisica e introdurre il principio di similitudine in quanto per questi complicati casi,non sono state   delineate né una teoria,né dei calcoli chiari e semplici.Bisogna allora procedere per esperimenti che di volta in volta daranno valori diversi tra loro di R.Da tali esperimenti risulta inoltre che R dipende dalle seguenti grandezze:scabrezza,diametro del tubo e numero di Reynolds. Risulta chiaro che se le tre grandezze sono uguali,non si necessita di molti esperimenti in quanto il risultato sarà sempre lo stesso,indipendentemente dal fluido preso in esame.

R= f ( DRe)

Apriamo un attimo una parentesi e definiamo la scabrezza .

Se prendiamo un tubo,ne ingrandiamo una parte ci accorgeremo che spesso le superfici dei condotti nei quali scorrono i fluidi,non sono lisce ma mostrano delle irregolarità dovute alla natura del materiale e ai procedimenti di realizzazione dei condotti stessi.La scabrezza risulta essere l'altezza tra gola e punta ossia quanto è discontinua la superficie.

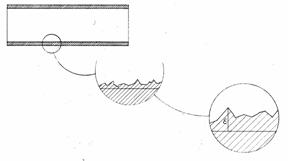
Nella seguente tabella sono mostrati i valori medi e gli intervalli di variabilità della scabrezza.

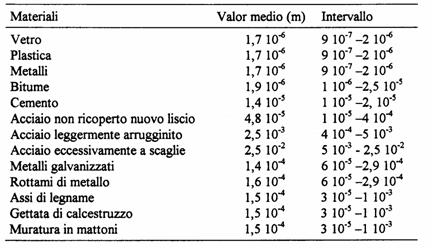
Ritornando alle perdite di carico distribuite,l'equazione per calcolarle risulta essere:

2

R= l L W  

D 2

l =coefficiente di attrito da calcolarsi caso per caso in quanto varia a seconda della sezione del

condotto (a sezione circolare) e della sua scabrezza.Si calcola cosi: 64

L Re

D   =lunghezza/diametro tubo

2

W  

2 =energia cinetica

Per un condotto a sezione circolare, il coefficiente di attrito per moto stabilizzato in funzione del numero di Reynolds e del parametro scabrezza, è rappresentato nel diagramma di Moody:

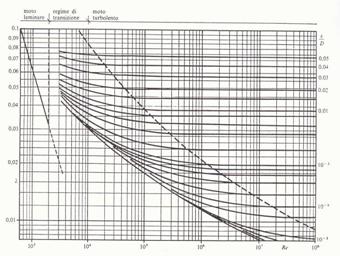
In questo diagramma sono riportati in ascissa il numero di Reynolds e in ordinata il fattore di attrito,entrambi in scala logaritmica.

Si noti che questo abaco è suddiviso in tre zone:

-nella prima il moto del fluido avviene per filetti paralleli (laminare) per cui la scabrezza del tubo non incide.Avremo allora numeri di Reynolds fino a 2300 e la curva sarà una retta.(caso poco comune,valido per oli combustibili con viscosità alta e bassa velocità)

-la seconda risulta essere una zona di transizione per la quale non si conosce l'andamento del diagramma.(ristretta e difficile da prevedere)

-la terza,la più comune,è definita dal regime turbolento e inizia per Re=4100. Qui la   scabrezza del tubo incide molto:più è scabro,più saranno le perdite.Solitamente si preferisce essere in questa zona in quanto si crea una situazione di scambio termico,ovvero in presenza di moto turbolento c'è un maggiore mescolamento che facilita il nascere di calore.

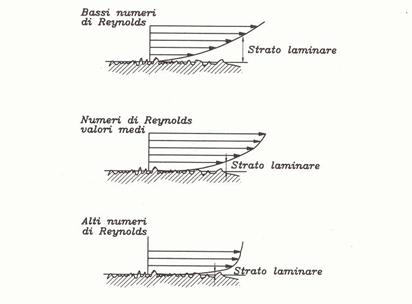
In questa ultima zona troveremo allora delle curve,curve che avranno un andamento discendente,tenderanno a spianarsi fino ad arrivare ad un andamento orizzontale.

Se in un problema vengono dati il fattore di scrabrezza del tubo e Re grazie al diagramma di Moody si può facilmente ricavare il valore del fattore d'attrito;basta tracciare una riga verticale che parte dal valore di Re e arriva alla curva che rappresenta la rugosità relativa del condotto e quindi dal quel punto tracciare una riga orizzontale fino al valore del fattore di attrito desiderato.Se il numero di Reynolds è un'incognita del problema si deve procedere alla risoluzione per tentativi.

Nel caso in cui non abbiamo un tubo cilindrico,ma di altre forme, sempre regolari,posso utilizzare le stesse formule e lo stesso diagramma introducendo però il concetto di diametro equivalente dato dal rapportotra quattro volte l'area della sezione e il perimetro bagnato (parte del tubo dove c'è contatto tra fluido e pareti)

ESECUZIONE DELLA PROVA

La prova consiste nel verificare le perdite di carico all'interno di tubi piezometrici e effettuata con una portata di acqua all'interno delle tubazioni pari a 180l/min.

ACCORGIMENTI PRELIMINARI

Dopo aver chiuso il rubinetto di scarico si procede all'azionamento della pompa centrifuga che favorisce il riempimento della vasca 1.

Nel nostro caso il livello nella vasca 1 è stato portato a 78 cm.

SVOLGIMRNTO DELLA PROVA

Si apre il rubinetto di scarico e si controlla sui manometri laterali che la portata nella tubazione rimanga costante (in questi manometri sono presenti due scale : una che moltiplica il valore letto per 130 e una che moltiplica il valore letto per 18 ).

A questo punto si vanno a riscontrare le tre altezze lungo la tubazione in corrispondenza degli appositi tubi per il rilevamento.

Una volta rilevate le tre altezze si procede calcolando le perdite di carico unitarie reali, delle perdite di carico teoriche (legge di Darcy) e del coefficiente di scabrezza.

DATI DELLA POMPA UTILIZZATA NELL' ESPERIENZA

(Pompa non volumetrica,centrifuga,non autoadescante)

Le tubazioni erano prive d'aria

Q=800-1600 l/min

H=53-54 m

Cv=25

Kw=18,4

PERDITA DI CARICO ALL'IMBOCCO

Z=

ξ =coefficiente all'imbocco =0,71

Dalla tabella risulta che la perdita continua è 1 cm y=9cm - 8cm = 1cm

PERDITA DI CARICO TEORICA

=

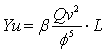
Perdita di carico sulle curve

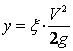
In cui assume valori sperimentali diversi in funzione del rapporto , in cui r rappresenta il raggio della curvatura, ed in funzione dell'angolo di deviazione .

Per > 4 la perdita di carico è trascurabile

Per ≤ 4 la perdita di carico si calcola assegnando al coefficiente il seguente valore: coefficiente delle perdite di carico localizzate

I valori del coefficiente sono dati in funzione dal rapporto

dato che il dato rilevato non è presente nella tabella prendiamo un valore di intermedio di fra 1,5 e 1: = 0,22

1° TUBO

2° TUBO

3°TUBO

PERDITE DI CARICO

(acqua entrante = acqua uscente)

Ø tubo=0,0508 m

V= 1,48 m/s  Qv=180 l/min=0,003 /s

sezione=

numero di Reynolds= temperature=10° C

pressione espressa in colonna d'acqua=   P=Pressione in Pascal

g=accelerazione di gravità

ρ=densità

scabrezza nei tubi da 100 cm =  120=perdita in mm

1000=lunghezza in

Scabrezza relativa =  E=scabrezza relativa

D=Ø tubo in mm

CALCOLO TEORICO SULLA TABELLA

Y=40 mm non è il tubo designato sulla tabella

CONCLUSIONI

L'esperienza svolta in laboratorio ha fatto capire come le perdite di carico si presentano e si distribuiscano nelle diverse tipologie di tubazioni

Hanno però inciso negativamente sull'esperienza presenta, fattori dei quali non si è tenuto conto, quali l'attrito, la scabrezza dei tubi piezometrici e le innumerevoli approssimazioni, quindi i risultati mostrano notevoli differenze tra i dati ottenuti sperimentalmente e quelli ottenuti teoricamente.

Nonostante tutto ciò,si può affermare che l'esperienza è stata chiara ed educativa e ha potuto far comprendere meglio l'argomento trattato.