|
|
| |
|
Il campo elettromagnetico: I parte |
|
|
|
|
|
|
Il campo elettromagnetico è l'universo elettrico.
I circuiti elettrici su cui, per la loro importanza tecnica, si è accentrata l'attenzione degli articoli precedenti, ne sono distribuzioni particolari: la loro struttura geometrica è sostanzialmente unidimensionale, cioè filiforme.
I due articoli finali esamineranno le grandezze del campo elettromagnetico in modo più generale, indagandone le proprietà in corpi di qualsiasi forma e dimensione.
Gli strumenti matematici per affrontarne lo studio sono i campi vettoriali. L'articolo ne enuncia, in forma semplificata, definizioni e proprietà, successivamente applicate al campo elettromagnetico.
Elementi di base dei campi vettoriali
Un vettore è un'entità matematica caratterizzata da un modulo, una direzione ed un verso. E' rappresentato da un segmento orientato. La lunghezza del segmento corrisponde al modulo del vettore, la freccia al verso, la retta cui il segmento appartiene, la direzione.
Il vettore è l'insieme di tutti i segmenti equipollenti (stessa direzione, stesso verso, stesso modulo). Il vettore applicato in un punto è rappresentato dal segmento avente l'origine in quel punto
Una porzione di spazio caratterizzata in ogni punto da una grandezza fisica rappresentabile con un vettore è un campo vettoriale.
Quando in ogni punto il vettore è lo stesso, il campo si dice uniforme.
Definizioni fondamentali sono:
prodotto scalare;
prodotto vettoriale
linea di forza;
integrale di linea;
flusso;
gradiente, divergenza, rotore.
E' un numero che corrisponde al prodotto dei moduli dei due vettori per il coseno dell'angolo che essi formano:
P= A1 . A2= A1.A2.cosa
Si può anche dire: è il prodotto del modulo di un vettore per la componente dell'altro secondo la retta orientata su cui giace il primo, fig. 9.1.a.
E' un vettore il cui modulo è il prodotto del modulo dei due vettori moltiplicato per il seno dell'angolo da essi formato, è perpendicolare al piano individuato dai due vettori, ed orientato secondo un osservatore che per sovrapporre il primo vettore al secondo descrivendo l'angolo tra di essi, deve ruotarlo in senso antiorario (fig. 9.1.b).
A= A1xA2
A=A1.A2.sina
E' la linea tangente in ogni punto al segmento che rap 151g65b presenta il vettore in quel punto. (fig. 9.1.c)
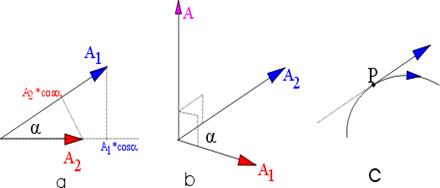
fig. 9 1
In un campo radiale le linee di forza partono da un centro per cui l'intensità del campo aumenta avvicinandosi al centro (la sorgente delle linee)
Definiamo l'operazione in un campo uniforme e per un segmento di retta. (fig. 9.2.a)
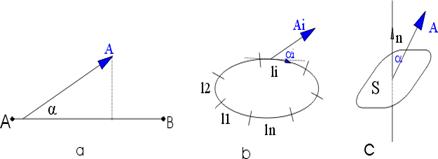
fig. 9 2
Si orienti il segmento che unisce due punti qualsiasi A, B, da A verso B. Sia a l'angolo che il segmento orientato forma con la direzione ed il verso del vettore del campo uniforme, A. Integrale di linea è il prodotto dell'intensità del vettore per la lunghezza del segmento lAB e per il coseno di a: UAB=A. lAB .cosa.
Se il campo non è uniforme ed il percorso che unisce i due punti non è un segmento di retta, si divide il percorso in n parti, ciascuna assimilabile ad un segmento di retta, per i cui punti il campo possa considerarsi costante. Per ognuno dei segmenti li così definiti, si effettua il calcolo precedente e, sommando gli n prodotti parziali, si ottiene l'integrale di linea, il cui valore è analiticamente esatto se n è molto grande.
Sintetizzando matematicamente:
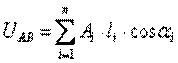 9.1
9.1
Quando B coincide con A ( linea chiusa) l'integrale di linea assume il nome di circuitazione (C). (fig. 9.2.b). I risultati del calcolo della circuitazione definiscono il tipo di campo.
Si consideri una superficie piana qualsiasi all'interno di un campo uniforme. Si tracci la perpendicolare, n, alla superficie e la si orienti, l'angolo che il vettore-campo (A) forma con la normale arbitrariamente. Sia a orientata. Il suo flusso attraverso la superficie è definito da:
F=A.S.cosa
dove S è l'area della superficie (fig. 9.2.c)
Nella raffigurazione del campo mediante linee di forza, il flusso può essere rappresentato dal numero di linee che attraversano la superficie S.
Se il campo non è uniforme e se la superficie non è piana, si suddivide la superficie in n parti, per i cui punti si possa ritenere il campo costante, si esegue per ognuna di esse il calcolo del flusso. Il flusso totale attraverso la superficie S è dato dall'espressione:
|
|
|
|
|
|
dove Ai è il modulo del vettore-campo per i punti della parte
di superficie Si ed ai è l'angolo che la
normale a questa superficie forma con il campo Ai .
Se la circuitazione del vettore-campo è nulla (C=0), il campo si dice conservativo. L'integrale di linea dipende allora solo dal punto iniziale e dal punto finale e non dal percorso. Si può definire una funzione scalare, detta potenziale, indicata con VP per il punto generico P, nota la quale è possibile calcolare l'integrale di linea facendo la differenza tra il valore assunto dalla funzione nel punto A e nel punto B, estremi della linea di calcolo: la 9.1 diventa
UAB=VA- VB. 9. 4
Le superfici in cui il potenziale è costante sono dette equipotenziali ed hanno la proprietà di essere in ogni punto perpendicolari alle linee di forza. Infatti presi due punti qualsiasi su di essa deve essere UAB= |90°|. Se si considerano due superfici =0, cioè, per la 9.1, a equipotenziali distanti d, si chiama gradiente di potenziale la differenza tra il potenziale dei punti della superficie 1 ed il potenziale dei punti della superficie 2 diviso la distanza:
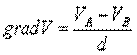 9.1
9.1
Si può porre in questo caso, indicato con A il vettore-campo:
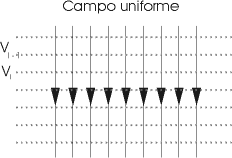 A= - grad V 9. 6
A= - grad V 9. 6
Un campo vettoriale si rappresenta mediante linee di forza e superfici equipotenziali.
Un campo uniforme è rappresentato in fig. 9.3 (le linee tratteggiate sono l'intersezione delle superfici equipotenziali con il piano del disegno)
NB: per la stessa definizione di gradiente, la circuitazione di un gradiente è nulla.
Divergenza di un vettore: div A
Se si calcola il flusso di un vettore attraverso una superficie chiusa si ottiene un valore diverso da zero solo se le linee di forza iniziano o finiscono in punti interni alla superficie. Rimpicciolendo la superficie fino ad identificarla con un punto, il flusso uscente è detto divergenza del vettore. Se è nullo significa che quel punto non è né inizio né fine di una linea di forza. Se ciò si verifica per tutti i punti il campo le linee di forza sono chiuse ed il campo si dice solenoidale.
Se la circuitazione di un vettore è diversa da zero si può definire un vettore che ha come modulo il valore della circuitazione e come direzione la perpendicolare alla superficie delimitata dalla linea di calcolo orientata secondo la regola della vite destrogira. Se la linea di calcolo rimpicciolisce fino a coincidere con il punto, il vettore non nullo che eventualmente si ottiene, si chiama rotore del vettore dato. Il suo flusso attraverso una superficie coincide con la circuitazione del vettore lungo la linea che delimita la superficie. L'esistenza del rotore significa per un campo che le sue linee di forza sono chiuse. La divergenza di un rotore è sempre nulla come il rotore di un gradiente: in quest'ultimo caso le linee hanno un inizio ed una fine.
Il campo elettrico nei materiali isolanti
La porzione di materia non conduttrice (dielettrico) in cui sono presenti cariche elettriche statiche, è sede di un campo vettoriale detto campo elettrostatico.
In esso sono presenti forze che possono agire su cariche elettriche. Il vettore che rappresenta in ogni punto la forza agente sull'unità di carica positiva è il campo elettrico: lo indicheremo con K. La sua unità di misura è il newton diviso coulomb:[N][C]-1
Le linee di forza dipendono dalla distribuzione delle cariche che producono il campo.
Hanno origine nelle cariche positive e terminano nelle cariche negative.
Coincidono con la traiettoria di una carica positiva puntiforme, che non alteri il campo preesistente, libera di muoversi (carica sonda).
Nella fig. 9.4 sono tracciati alcuni tipici campi. Il campo radiale prodotto da una carica Q distribuita uniformemente in un volume sferico (al limite di raggio nullo: carica puntiforme), (a); il campo prodotto da una carica positiva ed una uguale carica negativa (b), il campo di due cariche positive, il campo di una carica positiva uniformemente distribuita su una superficie piana (c), il campo prodotto da due superfici piane e parallele sulle quali è distribuita uniformemente la stessa carica avente però segno opposto (d).
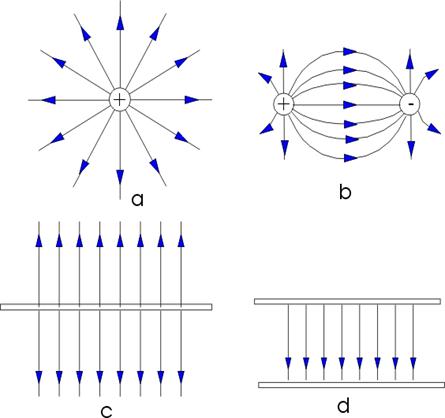
fig. 9 4
Tensione, potenziale e gradiente.
L'integrale di linea del campo elettrico K è la tensione elettrica che è' indipendente dal percorso scelto per il calcolo: il campo è conservativo. Per ogni punto del campo è definito il potenziale VP, la tensione tra due punti si trova eseguendo la differenza tra il potenziale dei due punti
UAB=VA-VB 9. 7
Il campo elettrico K è il gradiente di potenziale, cambiato di segno.
Dimensionalmente tensione e potenziale si misurano in joule diviso coulomb che è il volt:[V]=[J][C]-1
Il campo elettrico K si misura allora anche in volt diviso metro : [V]=[J][C]-1
Densità di spostamento, costante dielettrica, polarizzazione.
Il campo elettrico agisce sul materiale isolante, orientando i dipoli elettrici, cioè atomi o molecole nei quali si distinguono una zona positiva ed una negativa. L'entità di tale orientamento è misurabile dallo spostamento di carica ad esso conseguente all'orientamento. Si definisce il vettore densità di spostamento, indicato con D:che direzione e verso di K e modulo pari al rapporto tra la carica Q che, spostandosi, ha attraversato una superficie di area A, e l'area stessa: D=Q/A. Si misura in coulomb diviso metro quadro: [C][m]-2 ; dipende da K secondo un parametro, detto costante dielettrica , indicata con e, che caratterizza il materiale. Nel vuoto non esistono dipoli o cariche ma il campo elettrico possiede comunque un'intrinseca possibilità di provocare uno spostamento: questa possibilità è la densità di spostamento nel vuoto, che assume l'espressione:
D0 e K
in cui e0 è la costante dielettrica del vuoto (si misura in (coulomb diviso volt) diviso metro = farad diviso metro: [F][m]-1) che vale 8,85.10-12 F/m
Per un dielettrico materiale si avrà:
D=e K
D si compone sempre di due parti: quella dipendente dal materiale, detta polarizzazione ed indicata con P , che rappresenta l'effettivo numero di dipoli che si orientano; l'altra parte, indicata con D0, esiste anche in assenza di materiale. Si pone allora
D=D0+P=e K=P+e K
Flusso, circuitazione e rotore.
Il flusso di D attraverso una superficie chiusa è uguale alla carica contenuta all'interno della superficie: è la legge di Gauss. Indicando con Q la carica, con FD il flusso di D, con FK il flusso di K si ha:
Q = FD FK e
La circuitazione di D, quindi di K, è nulla per qualsiasi percorso: il rotore di K è dunque nullo.
Il campo elettrostatico è un serbatoio di energia potenziale elettrica. Il suo valore specifico, ricavabile dalla definizione di lavoro del campo quando una carica Q=D,A si sposta (joule diviso metro cubo, [J][m]-3) è dato dalle espressioni:
WE=0,5.K.D=0,5 e K2=0,5.D2/ e 9. 13
Negli isolanti reali materiali esistono cariche libere di muoversi. L'aumento dell'intensità di K le accelera finché la loro velocità assume un'energia tale da liberare ulteriori cariche nell'urto con le molecole del materiale. Si innesca una reazione a catena, accompagnata da intensi fenomeni termici e luminosi: è la scarica elettrica che compromette definitivamente le proprietà isolanti di un solido, mentre in un gas possono essere ripristinate quando la sollecitazione scompare.
Il valore del campo elettrico a cui si verifica il fenomeno della scarica è detto rigidità dielettrica del materiale: si misura in [V][m]-1. La rigidità di un materiale dipende dal suo grado di purezza, e dalle condizioni igrotermofisiche. Nella tab. 9.1 sono riportate le caratteristiche di alcuni materiali. La costante dielettrica relativa è il rapporto tra la costante dielettrica assoluta e la costante dielettrica del vuoto, quindi è un numero puro.
La rigidità è espressa in kV/mm=1MV/m
|
Isolante |
Costante dielettrica relativa |
Rigidità dielettrica [KV/mm] |
|
Aria secca (alla pressione di 1 [bar]) |
|
|
|
Carta comune |
|
|
|
Olio per trasformatori |
|
|
|
Polietilene |
|
|
|
Gomma |
|
|
|
Porcellana |
|
|
|
Bachelite |
|
|
|
Carta da condensatori |
|
|
|
Mica |
|
|
|
Vetro |
|
|
|
Acqua pura |
|
|
|
Ossido di titanio |
|
|
|
Titanati di Ba-Sr |
|
|
Tab 9.1
La struttura fondamentale del campo elettrostatico è il condensatore. Si potrebbe dire che è un contenitore di campo elettrostatico. Tecnicamente è costituito da due conduttori separati da un isolante. Quando un' armatura è dotata di carica positiva e l'altra di un'uguale carica negativa, l'isolante diviene sede di un campo elettrico.Tra le due armature si stabilisce una tensione U legata alla carica sulle armature da
Q=C.U 9. 14
C è la capacità del condensatore che dipende dalla natura fisica dell'isolante (costante dielettrica) e dalla geometria del campo imposta dalla forma delle armature.
Per armature piane e parallele di area A e distanti d (condensatore piano: struttura del campo 9.4.d) si ha (vedi anche art. 2)
![]()
Se le armature sono cilindriche di lunghezza l (condensatore cilindrico: es. cavo coassiale) indicate con ried re i raggi delle armature interna ed esterna, si ha
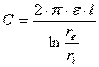
Se un'armatura è cilindrica e l'altra piana e sono parallele (es: linea rispetto al suolo), indicata con h la distanza con r il raggio ed l la lunghezza si ha
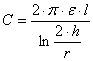
Se sono due cilindri distanti d di raggio r lunghi l (linea bifilare)
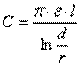
Se sono due sfere concentriche di raggio r1 ed r2 (condensatore sferico)
![]()
Se r2 è molto grande (sfera isolata: campo radiale fig. 9.4.a)
![]()
Energia immagazzinata nel condensatore
E' l'energia immagazzinata nel campo elettrico in esso presente. Sostanzialmente si moltiplica l'energia specifica media per il volume del campo. Si possono ottenere le espressioni.
WC=0,5.Q.U=0,5.C.U2=0,5.Q2/C
Es: nel condensatore piano il campo è uniforme, l'energia specifica WE è costante, è l'energia totale si ottiene moltiplicando WE (9.10) per il volume A.d del dielettrico. Quindi Wc=WE.A.d=0,5.K.D.A.d=0,5.Q.U essendo Q=D.A ed U=K.d
Carica e scarica di un condensatore.
Il formarsi del campo nel condensatore è un evento energetico: una energia prelevata, tramite il generatore da una fonte esterna, ed accumulata e conservata nel campo. In ogni sistema fisico le variazioni del suo stato energetico non sono mai istantanee, cioè non possono mai avvenire in un tempo nullo. Gli accumulatori di energia in esso presenti definiscono un parametro correlato al tempo necessario al sistema per evolvere da uno stato energetico all'altro. E' la costante di tempo. E' intuibile che il suo valore dipende dalla quantità di energia che può essere immagazzinata e dalle possibilità intrinseche del vettore energetico. Nel caso del condensatore la capacità C definisce le possibilità d'accumulo, mentre il vettore di energia è il conduttore attraverso cui fluisce la carica, caratterizzato dalla resistenza R. La costante di tempo è t=R.C. Le modalità di carica sono state esaminate alla fine dell'art. 6 (vedi fig. 6.15 a e 6.16 e relativi sviluppi matematici)
Il campo elettrico nei materiali conduttori
Questo tipo di campo è già stato esaminato: i circuiti elettrici sono un aspetto particolare del campo elettrico. In essi l'aspetto geometrico che il campo assume è filiforme, o ad una dimensione spaziale, quella secondo cui si sviluppano le linee di forza, che prevale nettamente sulle altre due. Le considerazioni che seguono valgono non solo per i circuiti già esaminati, come si metterà in evidenza, ma anche per geometrie di campo in cui ogni dimensione è ugualmente importante.
In un conduttore il campo elettrico è diverso da zero solo quando esistono delle sorgenti di energia: le forze elettromotrici. Si stabilisce allora un movimento di cariche attraverso il reticolo cristallino, accompagnato da dissipazione termica di energia. Il movimento permane se esiste la sorgente che fornisce l'energia dissipata: la f.e.m. appunto.
Densità di corrente, campo elettrico, conducibilità
Il vettore che descrive il movimento di cariche è la densità di corrente d misurata in ampere diviso metro quadro. E' proporzionale alla velocità di spostamento delle cariche (art. 1) che si stabilisce per l'equilibrio tra la forza d'attrito, proporzionale alla velocità, quindi alla densità di corrente, e la forza elettrica che agisce sull'unità di carica: il campo elettrico K. Si ha in definitiva
d g K
dove g è la caratteristica del conduttore chiamata conducibilità che si misura in siemens diviso metro: [S][m]-1.
Le linee di forza sono sempre chiuse e corrispondono alla componente del moto che le cariche libere hanno in comune.
L'integrale di linea del campo elettrico K rappresenta il lavoro fatto dal campo sull'unità di carica e dipende dal percorso per la possibile presenza di forze impresse, di natura elettromagnetica, meccanica, termica o chimica, agenti sull'unità di carica.
Definito il potenziale di un punto come l'energia dell'unità di carica in quel punto, la d.d.p. è data dall'energia ricevuta dall'unità di carica dalla sorgente della forza impressa agente lungo il percorso, diminuita del lavoro fatto dal campo elettrico.
Se E è la f.e.m. totale e costante agente lungo il percorso che unisce i punti A e B distanti l ed il campo elettrico totale K è costante, si può porre
UAB =VA-VB= E - K.l. 9. 23
Quindi dividendo per la lunghezza l
grad V = Ki - K 9. 24
Il campo elettrico totale K è allora dato da
dove si è posto:
Il flusso della densità di corrente d attraverso una superficie è l'intensità di corrente I.
Il flusso di d attraverso una superficie chiusa è nullo: il che significa che in un volume finito in cui è presente una corrente non vi può essere un accumulo di carica. E' ciò che corrisponde al primo principio di Kirchhoff che diventa in questo caso: divd=0: la divergenza del vettore densità di corrente è nulla.
In una porzione di conduttore di lunghezza l e sezione A, priva di forze impresse, essendo I=d A e K=-grad V=UAB/l , sostituendo nella 9.22 si ottiene la legge di Ohm. La 9.22 è dunque la legge di Ohm per le grandezze specifiche.
La circuitazione del vettore campo elettrico non è nulla e corrisponde alla totale forza elettromotrice agente lungo il percorso. Essa rappresenta dunque la variazione totale di energia delle cariche in movimento. Si ha, essendo nulla la circuitazione del gradiente di potenziale:
SK.l=SKi.l=SEi 9. 26
dalle 9.21, 9.23 si ottiene: Sr d l=S r (I/A).l =SE nella quale si riconosce il secondo principio di Kirchhoff: S R.I=SE (v. art. 3)
La struttura fondamentale: il resistore
La struttura tipica del campo di corrente è il resistore, una porzione di conduttore che fa capo a due estremità (elettrodi) tra le quali fluiscono le cariche. Il parametro che ne definisce le proprietà è la resistenza elettrica R (o il suo inverso: la conduttanza G) che dipende dal materiale, che viene i caratterizzato dalla sua resistività r (o il suo inverso: la conduttività g) (vedi. art.2) e dalla geometria degli elettrodi.
Il flusso di cariche tra gli elettrodi, cioè l'intensità di corrente, è, in assenza di f.e.m. lungo il percorso, proporzionale alla tensione tra gli elettrodi
I=G.U
L'identità formale della 9.21 con la 9.11 unita alla riflessione che non saremmo in grado di distinguere la "radiografia", se così si può dire, di un campo di corrente in un mezzo omogeneo da quella di un campo elettrostatico in un isolante, prodotti da elettrodi di geometria identica, ci fa capire come possiamo utilizzare le formule (9.12.9.17) per calcolare le conduttanze delle diverse geometrie: basta sostituire a e g a C, G.
La 9.12, riscritta come appena detto (quindi: G= g A/d), è la conduttanza di un conduttore prismatico (elettrodi paralleli di sezione A e distanti d); la 9.13 diventa la conduttanza di un cavo coassiale, serve dunque a determinarne la resistenza di isolamento; interessante infine è il caso di un elettrodo sferico che corrisponde ad esempio ad una sfera metallica immersa nel suolo in profondità e collegata con cavo isolato al polo di un generatore che ha pure l'altro polo collegato al suolo, a notevole distanza dall'elettrodo sferico. Si tratta della presa di terra ed il valore della resistenza di terra, che tanta importanza ha nei metodi per conseguire una utilizzazione sicura dell'energia elettrica, (ricavandola dalla 9.20) è dato da
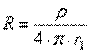
Il terreno è conduttore e la configurazione del campo elettrico che si stabilisce in esso per il fluire di correnti, o, ciò che è lo stesso, la configurazione delle linee di corrente, è molto importante ai fini della sicurezza elettrica, nella definizione delle tensioni di passo e di contatto.
La fig. 9.5 è mostra lo schema di una messa a terra, costituita da un dispersore sferico, cui è collegata una massa elettrica, cioè una parte conduttrice di un impianto elettrico che può, per un guasto dell'isolamento, venire in contatto con i conduttori attivi. In tal caso si ha una corrente che si disperde a terra: nella figura sono indicate le linee di forza (o di corrente), le superfici equipotenziali, il diagramma di potenziale in funzione della distanza dall'elettrodo, le tensioni di passo (UAB=VA-VB) e le tensioni di contatto (UMC=VM-VC).
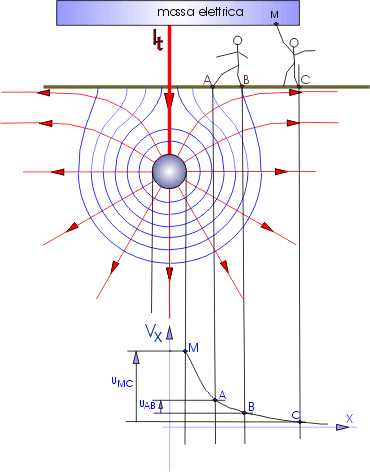
fig. 9. 5
Nei corpi materiali e nel vuoto possono essere presenti forze elettriche generate da una distribuzione di cariche ai bordi del volume considerato. Il campo elettrico assume configurazioni dipendenti dalla geometria della distribuzione producendo effetti energetici che dipendono dal materiale che occupa lo spazio. E' fondamentale saper riconoscere la configurazione: occorre tracciarne le linee di forza e, di conseguenza le superfici equipotenziali. I concetti esposti sui campi vettoriali lo consentono, anche se i procedimenti matematici necessari sono complessi e richiedono una trattazione molto più dettagliata di quella proposta. L'obiettivo dell'articolo era comunque di fornire le indicazioni di massima delle linee di indagine del campo elettrico nei corpi estesi.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026